机器学习基础——概率论

1. 概率的基本要素

为了定义集合上的概率，我们需要一些基本元素，

• 样本空间$\Omega$：随机实验的所有结果的集合。在这里，每个结果 $w \in \Omega$ 可以被认为是实验结束时现实世界状态的完整描述。

• 事件集（事件空间）$\mathcal{F}$：元素 $A \in \mathcal{F}$ 的集合（称为事件）是 $\Omega$ 的子集（即每个 $A \subseteq \Omega$ 是一个实验可能结果的集合）。

  备注：$\mathcal{F}$需要满足以下三个条件：

  (1) $\emptyset \in \mathcal{F}$

  (2) $A \in \mathcal{F} \Longrightarrow \Omega \backslash A \in \mathcal{F}$

  (3) $A_1,A_2,\cdots A_{i} \in \mathcal{F}\Longrightarrow\cup_{i} A_{i} \in \mathcal{F}$

• 概率度量$P$：函数$P$是一个$\mathcal{F} \rightarrow \mathbb{R}$的映射，满足以下性质：

  • 对于每个 $A \in \mathcal{F}$，$P(A) \geq 0$,

  • $P(\Omega) = 1$

  • 如果$A_1 ,A_2 ,\cdots$ 是互不相交的事件 (即 当$ i \neq j$时，$A_{i} \cap A_{j}=\emptyset$ ), 那么：

    $$P\left(\cup_{i} A_{i}\right)=\sum_{i} P\left(A_{i}\right)$$

以上三条性质被称为概率公理。

举例：

考虑投掷六面骰子的事件。样本空间为$\Omega= \{1，2，3，4，5，6\}$。最简单的事件空间是平凡事件空间$\mathcal{F} = \{\emptyset,\Omega\}$.另一个事件空间是$\Omega$的所有子集的集合。对于第一个事件空间，满足上述要求的唯一概率度量由$P(\emptyset) = 0$，$p(\Omega)= 1$给出。对于第二个事件空间，一个有效的概率度量是将事件空间中每个事件的概率分配为$i/6$，这里$i$ 是这个事件集合中元素的数量；例如$P(\{1,2,3,4\}) =4/6$，$P(\{1,2,3\}) =3/6$。

性质：

• 如果$A \subseteq B$，则：$P(A) \leq P(B)$
• $P(A \cap B) \leq min(P(A),P(B) )$
• (布尔不等式)：$P(A \cup B) \leq P(A)+P(B)$
• $P(\Omega |A ) =1-P(A)$
• (全概率定律)：如果$A_1，\cdots，A_k$是一些互不相交的事件并且它们的并集是$\Omega$，那么它们的概率之和是1

1.1 事件的关系与运算#

(1) 子事件：$A \subset B$，若$A$发生，则$B$发生。

(2) 相等事件：$A = B$，即$A \subset B$，且$B \subset A$ 。

(3) 和事件：$A\bigcup B$（或$A + B$），$A$与$B$中至少有一个发生。

(4) 差事件：$A - B$，$A$发生但$B$不发生。

(5) 积事件：$A\bigcap B$（或${AB}$），$A$与$B$同时发生。

(6) 互斥事件（互不相容）：$A\bigcap B$=$\varnothing$。

(7) 互逆事件（对立事件）：
$A\bigcap B=\varnothing ,A\bigcup B=\Omega ,A=\bar{B},B=\bar{A}$

1.2 运算律#

(1) 交换律：$A\bigcup B=B\bigcup A,A\bigcap B=B\bigcap A$
(2) 结合律：$(A\bigcup B)\bigcup C=A\bigcup (B\bigcup C)$
(3) 分配律：$(A\bigcap B)\bigcap C=A\bigcap (B\bigcap C)$

1.3 德$\centerdot$摩根律#

$\overline{A\bigcup B}=\bar{A}\bigcap \bar{B}$

$\overline{A\bigcap B}=\bar{A}\bigcup \bar{B}$

1.4 完全事件组#

${{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}$两两互斥，且和事件为必然事件，即${{A}_{i}}\bigcap {{A}_{j}}=\varnothing, i\ne j ,U_{i=1}^n = \Omega$

1.5 概率的基本公式#

(1)条件概率:
$P(A | B) \triangleq \frac{P(A \cap B)}{P(B)}$,表示$A$发生的条件下，$B$发生的概率。

(2)全概率公式：
$P(A)=\sum\limits_{i=1}^{n}{P(A|{{B}_{i}})P({{B}_{i}}),{{B}_{i}}{{B}_{j}}}=\varnothing ,i\ne j,\underset{i=1}{\overset{n}{\mathop{\bigcup }}}\,{{B}_{i}}=\Omega$

(3) Bayes 公式：

$$P({{B}_{j}}|A)=\frac{P(A|{{B}_{j}})P({{B}_{j}})}{\sum\limits_{i=1}^{n}{P(A|{{B}_{i}})P({{B}_{i}})}},j=1,2,\cdots ,n$$

注：上述公式中事件${{B}_{i}}$的个数可为可列个。

(4)乘法公式：
$P({{A}_{1}}{{A}_{2}})=P({{A}_{1}})P({{A}_{2}}|{{A}_{1}})=P({{A}_{2}})P({{A}_{1}}|{{A}_{2}})$
$P({{A}_{1}}{{A}_{2}}\cdots {{A}_{n}})=P({{A}_{1}})P({{A}_{2}}|{{A}_{1}})P({{A}_{3}}|{{A}_{1}}{{A}_{2}})\cdots P({{A}_{n}}|{{A}_{1}}{{A}_{2}}\cdots {{A}_{n-1}})$

1.6.事件的独立性#

(1)$A$与$B$相互独立

$\Leftrightarrow P(AB)=P(A)P(B)$

(2)$A$，$B$，$C$两两独立
$\Leftrightarrow P(AB)=P(A)P(B)$;$P(BC)=P(B)P(C)$ ;$P(AC)=P(A)P(C)$;

(3)$A$，$B$，$C$相互独立
$\Leftrightarrow P(AB)=P(A)P(B)$; $P(BC)=P(B)P(C)$ ;
$P(AC)=P(A)P(C)$ ; $P(ABC)=P(A)P(B)P(C)$

1.7 独立重复试验#

将某试验独立重复$n$次，若每次实验中事件 A 发生的概率为$p$，则$n$次试验中$A$发生$k$次的概率为：
$P(X=k)=C_{n}^{k}{{p}^{k}}{{(1-p)}^{n-k}}$

1.8 重要公式与结论#

$(1)P(\bar{A})=1-P(A)$

$(2)P(A\bigcup B)=P(A)+P(B)-P(AB)$
$P(A\bigcup B\bigcup C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)$

$(3)P(A-B)=P(A)-P(AB)$

$(4)P(A\bar{B})=P(A)-P(AB),P(A)=P(AB)+P(A\bar{B}),$
$P(A\bigcup B)=P(A)+P(\bar{A}B)=P(AB)+P(A\bar{B})+P(\bar{A}B)$

(5)条件概率$P(\centerdot |B)$满足概率的所有性质，
例如：. $P({{\bar{A}}_{1}}|B)=1-P({{A}_{1}}|B)$
$P({{A}_{1}}\bigcup {{A}_{2}}|B)=P({{A}_{1}}|B)+P({{A}_{2}}|B)-P({{A}_{1}}{{A}_{2}}|B)$
$P({{A}_{1}}{{A}_{2}}|B)=P({{A}_{1}}|B)P({{A}_{2}}|{{A}_{1}}B)$

(6)若${{A}_{1}},{{A}_{2}},\cdots ,{{A}_{n}}$相互独立，则$P(\bigcap\limits_{i=1}^{n}{{{A}_{i}}})=\prod\limits_{i=1}^{n}{P({{A}_{i}})},$
$P(\bigcup\limits_{i=1}^{n}{{{A}_{i}}})=\prod\limits_{i=1}^{n}{(1-P({{A}_{i}}))}$

(7)互斥、互逆与独立性之间的关系：
$A$与$B$互逆$\Rightarrow$ $A$与$B$互斥，但反之不成立，$A$与$B$互斥（或互逆）且均非零概率事件$\Rightarrow$$A$与$B$不独立.

(8)若${{A}_{1}},{{A}_{2}},\cdots ,{{A}_{m}},{{B}_{1}},{{B}_{2}},\cdots ,{{B}_{n}}$相互独立，则$f({{A}_{1}},{{A}_{2}},\cdots ,{{A}_{m}})$与$g({{B}_{1}},{{B}_{2}},\cdots ,{{B}_{n}})$也相互独立，其中$f(\centerdot ),g(\centerdot )$分别表示对相应事件做任意事件运算后所得的事件，另外，概率为 1（或 0）的事件与任何事件相互独立.

2. 随机变量

考虑一个实验，我们翻转10枚硬币，我们想知道正面硬币的数量。这里，样本空间$\Omega$的元素是长度为10的序列。例如，我们可能有$w_0 = \{H，H，T，H，T，H，H，T，T，T\}\in\Omega$。然而，在实践中，我们通常不关心获得任何特定正反序列的概率。相反，我们通常关心结果的实值函数，比如我们10次投掷中出现的正面数，或者最长的背面长度。在某些技术条件下，这些函数被称为随机变量。

更正式地说，随机变量$X$是一个的$\Omega \longrightarrow \mathbb{R}$函数。通常，我们将使用大写字母$X(\omega)$或更简单的$X$(其中隐含对随机结果$\omega$的依赖)来表示随机变量。我们将使用小写字母$x$来表示随机变量的值。

举例：
在我们上面的实验中，假设$X(\omega)$是在投掷序列$\omega$中出现的正面的数量。假设投掷的硬币只有10枚，那么$X(\omega)$只能取有限数量的值，因此它被称为离散随机变量。这里，与随机变量$X$相关联的集合取某个特定值$k$的概率为：

$$P(X=k) :=P(\{\omega : X(\omega) =k\})$$

举例：
假设$X(\omega)$是一个随机变量，表示放射性粒子衰变所需的时间。在这种情况下，$X(\omega)$具有无限多的可能值，因此它被称为连续随机变量。我们将$X$在两个实常数$a$和$b$之间取值的概率(其中$a < b$)表示为：

$$P(a \leq X \leq b) :=P(\{\omega : a \leq X(\omega) \leq b\})$$

2.1 累积分布函数#

为了指定处理随机变量时使用的概率度量，通常可以方便地指定替代函数(CDF、PDF和PMF)，在本节和接下来的两节中，我们将依次描述这些类型的函数。

累积分布函数(CDF)（简称分布函数）是函数$F_{X} : \mathbb{R} \rightarrow[0,1]$，它将概率度量指定为：

$$F_{X}(x) \triangleq P(X \leq x)$$

通过使用这个函数，我们可以计算任意事件发生的概率。图1显示了一个样本CDF函数。

图1：一个累计分布函数(CDF)

性质：

• $0 \leq F_{X}(x)\leq 1$
• $\lim _{x \rightarrow-\infty} F_{X}(x)=0$
• $\lim _{x \rightarrow\infty} F_{X}(x)=1$
• $x \leq y \Longrightarrow F_{X}(x)\leq F_{X}(y)$

2.2 概率质量函数#

当随机变量$X$取有限种可能值(即，$X$是离散随机变量)时，表示与随机变量相关联的概率度量的更简单的方法是直接指定随机变量可以假设的每个值的概率。特别地，概率质量函数(PMF)是函数 $p_{X} : \Omega \rightarrow \mathbb{R}$，这样：

$$p_{X}(x) \triangleq P(X=x)$$

在离散随机变量的情况下，我们使用符号$Val(X)$表示随机变量$X$可能假设的一组可能值。例如，如果$X(\omega)$是一个随机变量，表示十次投掷硬币中的正面数，那么$Val(X) =\{0，1，2，...，10\}$。

性质：

• $0 \leq p_{X}(x)\leq 1$
• $\sum_{x \in V \text { al }(X)} p_{X}(x)=1$
• $\sum_{x \in A} p_{X}(x)=P(X \in A)$

2.3 概率密度函数#

对于一些连续随机变量，累积分布函数$F_X (x)$处可微。在这些情况下，我们将概率密度函数(PDF)定义为累积分布函数的导数，即：

$$f_{X}(x) \triangleq \frac{d F_{X}(x)}{d x}$$

请注意，连续随机变量的概率密度函数可能并不总是存在的(即，如果它不是处处可微)。

根据微分的性质，对于很小的$\Delta x$，

$$P(x \leq X \leq x+\Delta x) \approx f_{X}(x) \Delta x$$

CDF和PDF(当它们存在时！)都可用于计算不同事件的概率。但是应该强调的是，任意给定点的概率密度函数(PDF)的值不是该事件的概率，即$f _X (x) \not = P(X = x)$。例如，$f _X (x)$可以取大于1的值(但是$f _X (x)$在$\mathbb{R}$的任何子集上的积分最多为1)。

性质：

• $f_X(x)\geq 0$
• $\int_{-\infty}^{\infty} f_{X}(x)=1$
• $\int_{x \in A} f_{X}(x) d x=P(X \in A)$

2.4 期望#

假设$X$是一个离散随机变量，其PMF为 $p_X (x)$，$g : \mathbb{R} \longrightarrow \mathbb{R}$是一个任意函数。在这种情况下，$g(X)$可以被视为随机变量，我们将$g(X)$的期望值定义为：

$$E[g(X)] \triangleq \sum_{x \in V a l(X)} g(x) p_{X}(x)$$

如果$X$是一个连续的随机变量，其PDF 为$f _X (x)$，那么$g(X)$的期望值被定义为：

$$E[g(X)] \triangleq \int_{-\infty}^{\infty} g(x) f_{X}(x) d x$$

直觉上，$g(X)$的期望值可以被认为是$g(x)$对于不同的$x$值可以取的值的“加权平均值”，其中权重由$p_X(x)$或$f_X(x)$给出。作为上述情况的特例，请注意，随机变量本身的期望值，是通过令$g(x) = x$得到的，这也被称为随机变量的平均值。

性质：

• 对于任意常数 $a \in \mathbb{R}$，$E[a]=a$
• 对于任意常数 $a \in \mathbb{R}$，$E[af(X)]=aE[f(X)]$
• (线性期望)：$E[f(X)+g(X)]=E[f(X)]+E[g(X)]$
• 对于一个离散随机变量$X$，$E[1\{X=k\}]=P(X=k)$

2.5 方差#

随机变量$X$的方差是随机变量$X$的分布围绕其平均值集中程度的度量。形式上，随机变量$X$的方差定义为：

$$\operatorname{Var}[X] \triangleq E\left[(X-E(X))^{2}\right]$$

使用上一节中的性质，我们可以导出方差的替代表达式:

$$\begin{aligned} E\left[(X-E[X])^{2}\right] &=E\left[X^{2}-2 E[X] X+E[X]^{2}\right] \\ &=E\left[X^{2}\right]-2 E[X] E[X]+E[X]^{2} \\ &=E\left[X^{2}\right]-E[X]^{2} \end{aligned}$$

其中第二个等式来自期望的线性，以及$E[X]$相对于外层期望实际上是常数的事实。

性质：

• 对于任意常数 $a \in \mathbb{R}$，$Val[a]=0$
• 对于任意常数 $a \in \mathbb{R}$，$Var[af(X)]=a^2Var[f(X)]$

举例：

计算均匀随机变量$X$的平均值和方差，任意$x \in [0，1]$，其PDF为 $p_X(x)= 1$，其他地方为0。

$$E[X]=\int_{-\infty}^{\infty} x f_{X}(x) d x=\int_{0}^{1} x d x=\frac{1}{2}$$

$$E\left[X^{2}\right]=\int_{-\infty}^{\infty} x^{2} f_{X}(x) d x=\int_{0}^{1} x^{2} d x=\frac{1}{3}$$

$$Var[X]=E[X^2]-E[X]^2=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$$

举例：

假设对于一些子集$A \subseteq \Omega$，有$g(x) = 1\{x \in A\}$，计算$E[g(X)]$?

离散情况：

$$E[g(X)]=\sum_{x \in V a l(X)} 1\{x \in A\} P_{X}(x) d x=\sum_{x \in A} P_{X}(x) d x=P(x \in A)$$

连续情况：

$$E[g(X)]=\int_{-\infty}^{\infty} 1\{x \in A\} f_{X}(x) d x=\int_{x \in A} f_{X}(x) d x=P(x \in A)$$

2.6 一些常见的随机变量#

离散随机变量

• 伯努利分布：硬币掷出正面的概率为$p$（其中：$0 \leq p \leq 1$），如果正面发生，则为1，否则为0。

  $$p(x)=\left\{\begin{array}{ll}{p} & {\text { if } p=1} \\ {1-p} & {\text { if } p=0}\end{array}\right.$$

• 二项式分布：掷出正面概率为$p$（其中：$0 \leq p \leq 1$）的硬币$n$次独立投掷中正面的数量。

  $$p(x)=\left(\begin{array}{l}{n} \\ {x}\end{array}\right) p^{x}(1-p)^{n-x}$$

• 泊松分布：用于模拟罕见事件频率的非负整数的概率分布（其中：$\lambda >0$）。

  $$p(x)=e^{-\lambda} \frac{\lambda^{x}}{x !}$$

• 几何分布：掷出正面概率为$p$（其中：$p >0$）的硬币第一次掷出正面所需要的次数。

  $$G(p):P(X = k) = {(1 - p)}^{k - 1}p,0 < p < 1,k = 1,2,\cdots.$$

• 超几何分布：$H(N,M,n):P(X = k) = \frac{C_{M}^{k}C_{N - M}^{n -k}}{C_{N}^{n}},k =0,1,\cdots,min(n,M)$

连续随机变量

• 均匀分布：在$a$和$b$之间每个点概率密度相等的分布（其中：$a<b$）。

  $$f(x)=\left\{\begin{array}{ll}{\frac{1}{b-a}} & {\text { if } a \leq x \leq b} \\ {0} & {\text { otherwise }}\end{array}\right.$$

• 指数分布：在非负实数上有衰减的概率密度（其中：$\lambda >0$）。

  $$f(x)=\left\{\begin{array}{ll}{\lambda e^{-\lambda x}} & {\text { if } x \geq 0} \\ {0} & {\text { otherwise }}\end{array}\right.$$

• 正态分布：又被称为高斯分布。

  $$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}}$$

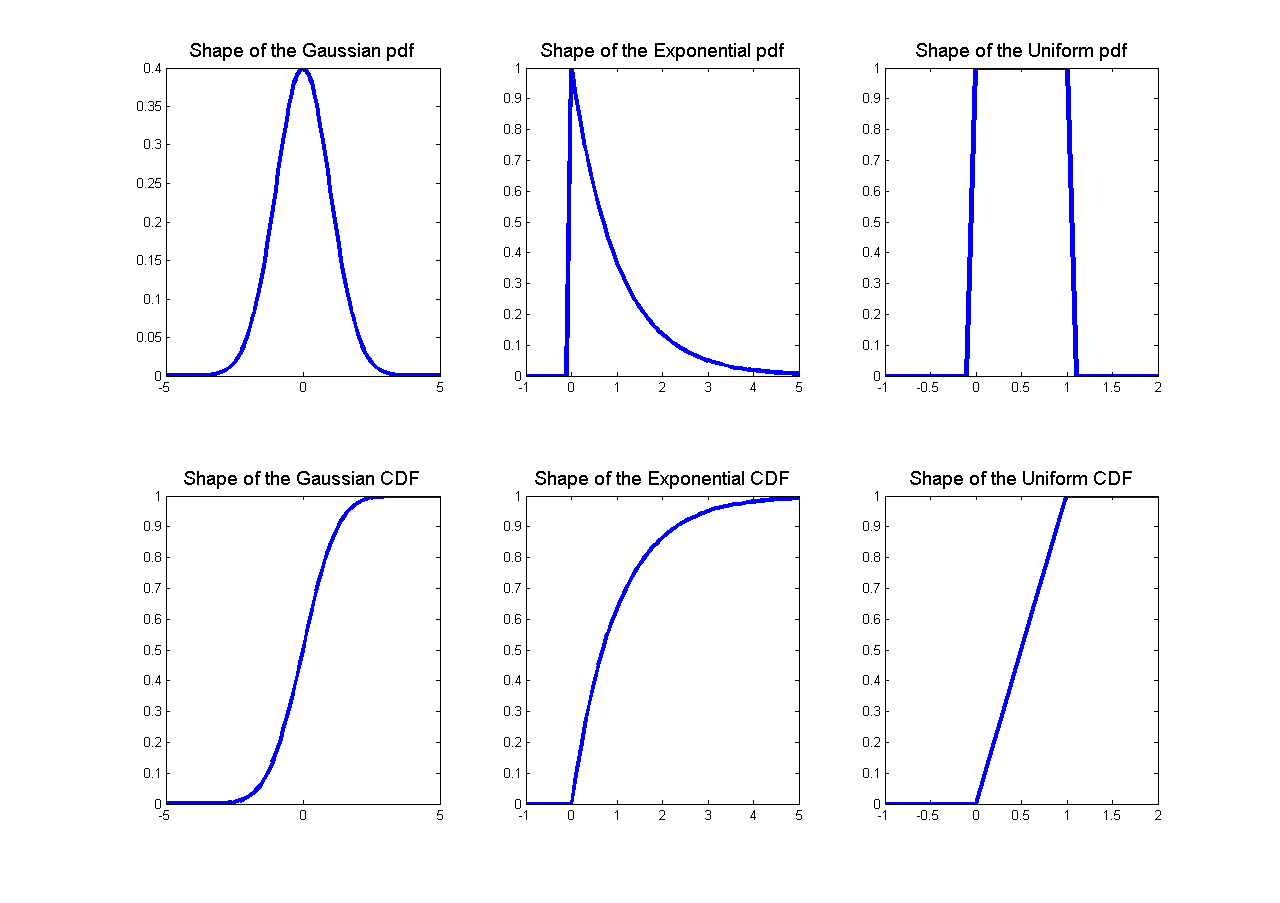
一些随机变量的概率密度函数和累积分布函数的形状如图2所示。

图2：一些随机变量的概率密度函数(PDF)和累积分布函数(CDF)

下表总结了这些分布的一些特性：

分布	概率密度函数(PDF)或者概率质量函数(PMF)	均值	方差
$Bernoulli(p)$(伯努利分布)	$\left\{\begin{array}{ll}{p} & {\text { if } x=1} \\ {1-p} & {\text { if } x=0}\end{array}\right.$	$p$	$p(1-p)$
$Binomial(n,p)$(二项式分布)	$\left(\begin{array}{l}{n} \\ {k}\end{array}\right) p^{k}(1-p)^{n-k}$ 其中：$0 \leq k \leq n$	$np$	$npq$
$Geometric(p)$(几何分布)	$p(1-p)^{k-1}$ 其中：$k=1,2,\cdots$	$\frac{1}{p}$	$\frac {1-p}{p^2}$
$Poisson(\lambda)$(泊松分布)	$e^{-\lambda} \lambda^{x} / x !$ 其中：$k=1,2,\cdots$	$\lambda$	$\lambda$
$Uniform(a,b)$(均匀分布)	$\frac{1}{b-a}$ 存在$x \in (a,b)$	$\frac{a+b}{2}$	$\frac{(b-a)^2}{12}$
$Gaussian(\mu,\sigma^2)$(高斯分布)	$\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}}$	$\mu$	$\sigma^2$
$Exponential(\lambda)$(指数分布)	$\lambda e^{-\lambda x}$ $x\geq0,\lambda>0$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$

2.7 重要公式与结论#

(1) $X\sim N(0,1) \Rightarrow \varphi(0) = \frac{1}{\sqrt{2\pi}},\Phi(0) =\frac{1}{2},$ $\Phi( - a) = P(X \leq - a) = 1 - \Phi(a)$

(2) $X\sim N\left( \mu,\sigma^{2} \right) \Rightarrow \frac{X -\mu}{\sigma}\sim N\left( 0,1 \right),P(X \leq a) = \Phi(\frac{a -\mu}{\sigma})$

(3) $X\sim E(\lambda) \Rightarrow P(X > s + t|X > s) = P(X > t)$

(4) $X\sim G(p) \Rightarrow P(X = m + k|X > m) = P(X = k)$

(5) 离散型随机变量的分布函数为阶梯间断函数；连续型随机变量的分布函数为连续函数，但不一定为处处可导函数。

(6) 存在既非离散也非连续型随机变量。

3. 两个随机变量

到目前为止，我们已经考虑了单个随机变量。然而，在许多情况下，在随机实验中，我们可能有不止一个感兴趣的量。例如，在一个我们掷硬币十次的实验中，我们可能既关心$X(\omega) =$出现的正面数量，也关心$Y (\omega) =$连续最长出现正面的长度。在本节中，我们考虑两个随机变量的设置。

3.1 联合分布和边缘分布#

假设我们有两个随机变量，一个方法是分别考虑它们。如果我们这样做，我们只需要$F_X (x)$和$F_Y (y)$。但是如果我们想知道在随机实验的结果中，$X$和$Y$同时假设的值，我们需要一个更复杂的结构，称为$X$和$Y$的联合累积分布函数，定义如下:

$$F_{XY}(x,y)=P(X \leq x,Y \leq y)$$

可以证明，通过了解联合累积分布函数，可以计算出任何涉及到$X$和$Y$的事件的概率。

联合CDF: $F_{XY }(x,y)$和每个变量的联合分布函数$F_X(x)$和$F_Y (y)$分别由下式关联:

$$F_{X}(x)=\lim _{y \rightarrow \infty} F_{X Y}(x, y) d y$$

$$F_{Y}(y)=\lim _{y \rightarrow \infty} F_{X Y}(x, y) dx$$

这里我们称$F_X(x)$和$F_Y (y)$为 $F_{XY }(x,y)$的边缘累积概率分布函数。

性质：

• $0 \leq F_{XY }(x,y) \leq 1$
• $\lim _{x, y \rightarrow \infty} F_{X Y}(x, y)=1$
• $\lim _{x, y \rightarrow -\infty} F_{X Y}(x, y)=0$
• $F_{X}(x)=\lim _{y \rightarrow \infty} F_{X Y}(x, y)$

3.2 联合概率和边缘概率质量函数#

如果$X$和$Y$是离散随机变量，那么联合概率质量函数 $p_{X Y} : \mathbb{R} \times \mathbb{R} \rightarrow [0,1]$由下式定义：

$$p_{X Y}(x,y)=P(X=x,Y=y)$$

这里, 对于任意$x$，$y$，$0 \leq P_{XY} (x,y) \leq 1$, 并且 $\sum_{x \in V a l(X)} \sum_{y \in V a l(Y)} P_{X Y}(x, y)=1$

两个变量上的联合PMF分别与每个变量的概率质量函数有什么关系？事实上：

$$p_{X}(x)=\sum_{y} p_{X Y}(x, y)$$

对于$p_Y (y)$类似。在这种情况下，我们称$p_X(x)$为$X$的边际概率质量函数。在统计学中，将一个变量相加形成另一个变量的边缘分布的过程通常称为“边缘化”。

3.3 联合概率和边缘概率密度函数#

假设$X$和$Y$是两个连续的随机变量，具有联合分布函数$F_{XY}$。在$F_{XY}(x,y)$在$x$和$y$中处处可微的情况下，我们可以定义联合概率密度函数：

$$f_{X Y}(x, y)=\frac{\partial^{2} F_{X Y}(x, y)}{\partial x \partial y}$$

如同在一维情况下，$f_{XY}(x,y)\not= P(X = x,Y = y)$，而是：

$$\iint_{x \in A} f_{X Y}(x, y) d x d y=P((X, Y) \in A)$$

请注意，概率密度函数$f_{XY}(x,y)$的值总是非负的，但它们可能大于1。尽管如此，可以肯定的是 $\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_{X Y}(x, y)=1$

与离散情况相似，我们定义:

$$f_{X}(x)=\int_{-\infty}^{\infty} f_{X Y}(x, y) d y$$

作为$X$的边际概率密度函数(或边际密度)，对于$f_Y (y)$也类似。

3.4 条件概率分布#

条件分布试图回答这样一个问题，当我们知道$X$必须取某个值$x$时，$Y$上的概率分布是什么？在离散情况下，给定$Y$的条件概率质量函数是简单的：

$$p_{Y | X}(y | x)=\frac{p_{X Y}(x, y)}{p_{X}(x)}$$

假设分母不等于0。

在连续的情况下，在技术上要复杂一点，因为连续随机变量的概率等于零。忽略这一技术点，我们通过类比离散情况，简单地定义给定$X = x$的条件概率密度为：

$$f_{Y | X}(y | x)=\frac{f_{X Y}(x, y)}{f_{X}(x)}$$

假设分母不等于0。

3.5 贝叶斯定理#

当试图推导一个变量给定另一个变量的条件概率表达式时，经常出现的一个有用公式是贝叶斯定理。

对于离散随机变量$X$和$Y$：

$$P_{Y | X}(y | x)=\frac{{P_{XY}}(x, y)}{P_{X}(x)}=\frac{P_{X | Y}(x | y) P_{Y}(y)}{\sum_{y^{\prime} \in V a l(Y)} P_{X | Y}\left(x | y^{\prime}\right) P_{Y}\left(y^{\prime}\right)}$$

对于连续随机变量$X$和$Y$：

$$f_{Y | X}(y | x)=\frac{f_{X Y}(x, y)}{f_{X}(x)}=\frac{f_{X | Y}(x | y) f_{Y}(y)}{\int_{-\infty}^{\infty} f_{X | Y}\left(x | y^{\prime}\right) f_{Y}\left(y^{\prime}\right) d y^{\prime}}$$

3.6 独立性#

如果对于$X$和$Y$的所有值，$F_{XY}(x,y) = F_X(x)F_Y(y)$，则两个随机变量$X$和$Y$是独立的。等价地，

• 对于离散随机变量, 对于任意$x \in Val(X)$, $y \in Val(Y)$ ，$p_{XY}(x,y) = p_X (x)p_Y (y)$。
• 对于离散随机变量, $p_Y |X (y|x) = p_Y (y)$当对于任意$y \in Val(Y)$且$p_X (x) \not= 0$。
• 对于连续随机变量, $f_{XY}(x,y) = f_X (x)f_Y(y)$ 对于任意 $x,y \in \mathbb{R}$。
• 对于连续随机变量, $f_{Y |X} (y|x) = f_Y (y)$ ，当$f_X (x)\not = 0$对于任意$y \in \mathbb{R}$。

非正式地说，如果“知道”一个变量的值永远不会对另一个变量的条件概率分布有任何影响，那么两个随机变量$X$和$Y$是独立的，也就是说，你只要知道$f(x)$和$f(y)$就知道关于这对变量$(X，Y)$的所有信息。以下引理将这一观察形式化:

引理3.1

如果$X$和$Y$是独立的，那么对于任何$A，B⊆ \mathbb{R}$，我们有：

$$P(X \in A, Y \in B)=P(X \in A) P(Y \in B)$$

利用上述引理，我们可以证明如果$X$与$Y$无关，那么$X$的任何函数都与$Y$的任何函数无关。

3.7 期望和协方差#

假设我们有两个离散的随机变量$X$，$Y$并且$g : \mathbf{R}^{2} \longrightarrow \mathbf{R}$是这两个随机变量的函数。那么$g$的期望值以如下方式定义：

$$E[g(X, Y)] \triangleq \sum_{x \in V a l(X)} \sum_{y \in V a l(Y)} g(x, y) p_{X Y}(x, y)$$

对于连续随机变量$X$，$Y$，类似的表达式是：

$$E[g(X, Y)]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g(x, y) f_{X Y}(x, y) d x d y$$

我们可以用期望的概念来研究两个随机变量之间的关系。特别地，两个随机变量的协方差定义为：

$${Cov}[X, Y] \triangleq E[(X-E[X])(Y-E[Y])]$$

使用类似于方差的推导，我们可以将它重写为：

$$\begin{aligned} {Cov}[X, Y] &=E[(X-E[X])(Y-E[Y])] \\ &=E[X Y-X E[Y]-Y E[X]+E[X] E[Y]] \\ &=E[X Y]-E[X] E[Y]-E[Y] E[X]+E[X] E[Y]] \\ &=E[X Y]-E[X] E[Y] \end{aligned}$$

在这里，说明两种协方差形式相等的关键步骤是第三个等号，在这里我们使用了这样一个事实，即$E[X]$和$E[Y]$实际上是常数，可以被提出来。当$cov[X，Y] = 0$时，我们说$X$和$Y$不相关。

性质：

• (期望线性) $E[f(X,Y ) + g(X,Y)] = E[f(X,Y )] + E[g(X,Y)]$
• $V ar[X + Y ] = V ar[X] + V ar[Y ] + 2Cov[X,Y]$
• 如果$X$和$Y$相互独立, 那么 $Cov[X,Y ] = 0$
• 如果$X$和$Y$相互独立, 那么 $E[f(X)g(Y )] = E[f(X)]E[g(Y)]$.

3.8 常见的二维随机变量#

(1) 二维均匀分布：$(x,y) \sim U(D)$ ,$f(x,y) = \begin{cases} \frac{1}{S(D)},(x,y) \in D \\ 0,其他 \end{cases}$

(2) 二维正态分布：$(X,Y)\sim N(\mu_{1},\mu_{2},\sigma_{1}^{2},\sigma_{2}^{2},\rho)$,$(X,Y)\sim N(\mu_{1},\mu_{2},\sigma_{1}^{2},\sigma_{2}^{2},\rho)$

$f(x,y) = \frac{1}{2\pi\sigma_{1}\sigma_{2}\sqrt{1 - \rho^{2}}}.\exp\left\{ \frac{- 1}{2(1 - \rho^{2})}\lbrack\frac{{(x - \mu_{1})}^{2}}{\sigma_{1}^{2}} - 2\rho\frac{(x - \mu_{1})(y - \mu_{2})}{\sigma_{1}\sigma_{2}} + \frac{{(y - \mu_{2})}^{2}}{\sigma_{2}^{2}}\rbrack \right\}$

3.9 重要公式与结论#

(1) 边缘密度公式： $f_{X}(x) = \int_{- \infty}^{+ \infty}{f(x,y)dy,}$
$f_{Y}(y) = \int_{- \infty}^{+ \infty}{f(x,y)dx}$

(2) $P\left\{ \left( X,Y \right) \in D \right\} = \iint_{D}^{}{f\left( x,y \right){dxdy}}$

(3) 若$(X,Y)$服从二维正态分布$N(\mu_{1},\mu_{2},\sigma_{1}^{2},\sigma_{2}^{2},\rho)$
则有：

1. $X\sim N\left( \mu_{1},\sigma_{1}^{2} \right),Y\sim N(\mu_{2},\sigma_{2}^{2}).$

2. $X$与$Y$相互独立$\Leftrightarrow \rho = 0$，即$X$与$Y$不相关。

3. $C_{1}X + C_{2}Y\sim N(C_{1}\mu_{1} + C_{2}\mu_{2},C_{1}^{2}\sigma_{1}^{2} + C_{2}^{2}\sigma_{2}^{2} + 2C_{1}C_{2}\sigma_{1}\sigma_{2}\rho)$

4. ${\ X}$关于$Y=y$的条件分布为： $N(\mu_{1} + \rho\frac{\sigma_{1}}{\sigma_{2}}(y - \mu_{2}),\sigma_{1}^{2}(1 - \rho^{2}))$

5. $Y$关于$X = x$的条件分布为： $N(\mu_{2} + \rho\frac{\sigma_{2}}{\sigma_{1}}(x - \mu_{1}),\sigma_{2}^{2}(1 - \rho^{2}))$

(4) 若$X$与$Y$独立，且分别服从$N(\mu_{1},\sigma_{1}^{2}),N(\mu_{1},\sigma_{2}^{2}),$
则：$\left( X,Y \right)\sim N(\mu_{1},\mu_{2},\sigma_{1}^{2},\sigma_{2}^{2},0),$

$C_{1}X + C_{2}Y\tilde{\ }N(C_{1}\mu_{1} + C_{2}\mu_{2},C_{1}^{2}\sigma_{1}^{2} C_{2}^{2}\sigma_{2}^{2}).$

(5) 若$X$与$Y$相互独立，$f\left( x \right)$和$g\left( x \right)$为连续函数， 则$f\left( X \right)$和$g(Y)$也相互独立。

4. 多个随机变量

上一节介绍的概念和想法可以推广到两个以上的随机变量。特别是，假设我们有$n$个连续随机变量，$X _1 (\omega),X_2 (\omega),\cdots X_n (\omega)$。在本节中，为了表示简单，我们只关注连续的情况，对离散随机变量的推广工作类似。

4.1 基本性质#

我们可以定义$X_1,X_2,\cdots,X_n$的联合累积分布函数、联合概率密度函数，以及给定$X_2,\cdots,X_n$时$X_1$的边缘概率密度函数为：

$$F_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)=P\left(X_{1} \leq x_{1}, X_{2} \leq x_{2}, \ldots, X_{n} \leq x_{n}\right)$$

$$f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)=\frac{\partial^{n} F_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)}{\partial x_{1} \ldots \partial x_{n}}$$

$$f_{X_{1}}\left(X_{1}\right)=\int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{2} \ldots d x_{n}$$

$$f_{X_{1} | X_{2}, \ldots, X_{n}}\left(x_{1} | x_{2}, \dots x_{n}\right)=\frac{f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \dots x_{n}\right)}{f_{X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right)}$$

为了计算事件$A \subseteq \mathbb{R}^{n}$的概率，我们有：

$$P\left(\left(x_{1}, x_{2}, \ldots x_{n}\right) \in A\right)=\int_{\left(x_{1}, x_{2}, \ldots x_{n}\right) \in A} f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}$$

链式法则：

从多个随机变量的条件概率的定义中，可以看出：

$$\begin{aligned} f\left(x_{1}, x_{2}, \ldots, x_{n}\right) &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{1}, x_{2} \ldots, x_{n-1}\right) \\ &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{n-1} | x_{1}, x_{2} \ldots, x_{n-2}\right) f\left(x_{1}, x_{2} \ldots, x_{n-2}\right) \\ &=\cdots=f\left(x_{1}\right) \prod_{i=2}^{n} f\left(x_{i} | x_{1}, \ldots, x_{i-1}\right) \end{aligned}$$

独立性:对于多个事件，$A_1,\cdots ,A_k$,我们说$A_1,\cdots ,A_k$ 是相互独立的,当对于任何子集$S \subseteq \{1，2,\cdots,k\}$，我们有：

$$P\left(\cap_{i \in S} A_{i}\right)=\prod_{i \in S} P\left(A_{i}\right)$$

同样，我们说随机变量$X_1,X_2,\cdots,X_n$是独立的，如果：

$$f(x_1,\cdots,x_n)=f(x_1)f(x_2)\cdots f(x_n)$$

这里，相互独立性的定义只是两个随机变量独立性到多个随机变量的自然推广。

独立随机变量经常出现在机器学习算法中，其中我们假设属于训练集的训练样本代表来自某个未知概率分布的独立样本。为了明确独立性的重要性，考虑一个“坏的”训练集，我们首先从某个未知分布中抽取一个训练样本$(x^{ (1)},y^{(1)})$，然后将完全相同的训练样本的$m-1$个副本添加到训练集中。在这种情况下，我们有：

$$P\left(\left(x^{(1)}, y^{(1)}\right), \ldots .\left(x^{(m)}, y^{(m)}\right)\right) \neq \prod_{i=1}^{m} P\left(x^{(i)}, y^{(i)}\right)$$

尽管训练集的大小为$m$，但这些例子并不独立！虽然这里描述的过程显然不是为机器学习算法建立训练集的明智方法，但是事实证明，在实践中，样本的不独立性确实经常出现，并且它具有减小训练集的“有效大小”的效果。

4.2 随机向量#

假设我们有n个随机变量。当把所有这些随机变量放在一起工作时，我们经常会发现把它们放在一个向量中是很方便的...我们称结果向量为随机向量(更正式地说，随机向量是从$\Omega$到$\mathbb{R}^n$的映射)。应该清楚的是，随机向量只是处理$n$个随机变量的一种替代符号，因此联合概率密度函数和综合密度函数的概念也将适用于随机向量。

期望:

考虑$g : \mathbb{R}^n \rightarrow \mathbb{R}$中的任意函数。这个函数的期望值 被定义为

$$E[g(X)]=\int_{\mathbb{R}^{n}} g\left(x_{1}, x_{2}, \ldots, x_{n}\right) f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}E[g(X)]\\=\int_{\mathbb{R}^{n}} g\left(x_{1}, x_{2}, \ldots, x_{n}\right) f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots x_{n}\right) d x_{1} d x_{2} \ldots d x_{n}$$

其中，$\int_{\mathbb{R}^{n}}$是从$-\infty$到$\infty$的$n$个连续积分。如果$g$是从$\mathbb{R}^n$到$\mathbb{R}^m$的函数，那么$g$的期望值是输出向量的元素期望值，即，如果$g$是：

$$g(x)=\left[\begin{array}{c}{g_{1}(x)} \\ {g_{2}(x)} \\ {\vdots} \\ {g_{m}(x)}\end{array}\right]$$

那么，

$$E[g(X)]=\left[\begin{array}{c}{E\left[g_{1}(X)\right]} \\ {E\left[g_{2}(X)\right]} \\ {\vdots} \\ {E\left[g_{m}(X)\right]}\end{array}\right]$$

协方差矩阵：对于给定的随机向量$X:\Omega\rightarrow \mathbb{R}^n$，其协方差矩阵$\Sigma$是$n \times n$平方矩阵，其输入由$\Sigma_{i j}={Cov}\left[X_{i}, X_{j}\right]$给出。从协方差的定义来看，我们有：

$$\begin{aligned} \begin{equation} \Sigma=\left[\begin{array}{ccc}{{Cov}\left[X_{1}, X_{1}\right]} & {\cdots} & {{Cov}\left[X_{1}, X_{n}\right]} \\ {\vdots} & {\ddots} & {\vdots} \\ {{Cov}\left[X_{n}, X_{1}\right]} & {\cdots} & {{Cov}\left[X_{n}, X_{n}\right]}\end{array}\right]\\ =\left[\begin{array}{ccc}{E\left[X_{1}^{2}\right]-E\left[X_{1}\right] E\left[X_{1}\right]} & {\cdots} & {E\left[X_{1} X_{n}\right]-E\left[X_{1}\right] E\left[X_{n}\right]} \\ {\vdots} & {\ddots} & {\vdots} \\ {E\left[X_{n} X_{1}\right]-E\left[X_{n}\right] E\left[X_{1}\right]} & {\cdots} & {E\left[X_{n}^{2}\right]-E\left[X_{n}\right] E\left[X_{n}\right]}\end{array}\right]\\ =\left[\begin{array}{ccc}{E\left[X_{1}^{2}\right]} & {\cdots} & {E\left[X_{1} X_{n}\right]} \\ {\vdots} & {\ddots} & {\vdots} \\ {E\left[X_{n} X_{1}\right]} & {\cdots} & {E\left[X_{n}^{2}\right]}\end{array}\right]-\left[\begin{array}{ccc}{E\left[X_{1}\right] E\left[X_{1}\right]} & {\cdots} & {E\left[X_{1}\right] E\left[X_{n}\right]} \\ {\vdots} & {\ddots} & {\vdots} \\ {E\left[X_{n}\right] E\left[X_{1}\right]} & {\cdots} & {E\left[X_{n}\right] E\left[X_{n}\right]}\end{array}\right]\\ =E\left[X X^{T}\right]-E[X] E[X]^{T}=\ldots=E\left[(X-E[X])(X-E[X])^{T}\right] \end{equation} \end{aligned}$$

其中矩阵期望以明显的方式定义。
协方差矩阵有许多有用的属性:

• $\Sigma \succeq 0$；也就是说，$\Sigma$是正半定的。
• $\Sigma=\Sigma^T$；也就是说，$\Sigma$是对称的。

4.3 多元高斯分布#

随机向量上概率分布的一个特别重要的例子叫做多元高斯或多元正态分布。随机向量$X\in \mathbb{R}^n$被认为具有多元正态(或高斯)分布，当其具有均值$\mu \in \mathbb{R}^n$和协方差矩阵$\Sigma \in \mathbb{S}_{++}^{n}$(其中$ \mathbb{S}_{++}^{n}$指对称正定$n \times n$矩阵的空间)

$f_{X_{1}, X_{2}, \ldots, X_{n}}\left(x_{1}, x_{2}, \ldots, x_{n} ; \mu, \Sigma\right)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right)$

我们把它写成$X \sim \mathcal{N}(\mu, \Sigma)$。请注意，在$n = 1$的情况下，它降维成普通正态分布，其中均值参数为$\mu_1$，方差为$\Sigma_{11}$。

一般来说，高斯随机变量在机器学习和统计中非常有用，主要有两个原因：

首先，在统计算法中对“噪声”建模时，它们非常常见。通常，噪声可以被认为是影响测量过程的大量小的独立随机扰动的累积；根据中心极限定理，独立随机变量的总和将趋向于“看起来像高斯”。

其次，高斯随机变量便于许多分析操作，因为实际中出现的许多涉及高斯分布的积分都有简单的封闭形式解。我们将在本课程稍后遇到这种情况。

5. 随机变量的数字特征

一些具体的推导前文有过详细的阐述，这里不加缀述，此处仅作总结用

5.1 数学期望#

离散型：$P\left\{ X = x_{i} \right\} = p_{i},E(X) = \sum_{i}^{}{x_{i}p_{i}}$；

连续型： $X\sim f(x),E(X) = \int_{- \infty}^{+ \infty}{xf(x)dx}$

性质：

(1) $E(C) = C,E\lbrack E(X)\rbrack = E(X)$

(2) $E(C_{1}X + C_{2}Y) = C_{1}E(X) + C_{2}E(Y)$

(3) 若$X$和$Y$独立，则$E(XY) = E(X)E(Y)$

(4)$\left\lbrack E(XY) \right\rbrack^{2} \leq E(X^{2})E(Y^{2})$

5.2 方差：#

$D(X) = E\left\lbrack X - E(X) \right\rbrack^{2} = E(X^{2}) - \left\lbrack E(X) \right\rbrack^{2}$

5.3 标准差：#

• 离散型：$D(X) = \sum_{i}^{}{\left\lbrack x_{i} - E(X) \right\rbrack^{2}p_{i}}$
• 连续型：$D(X) = {\int_{- \infty}^{+ \infty}\left\lbrack x - E(X) \right\rbrack}^{2}f(x)dx$

性质：

(1)$\ D(C) = 0,D\lbrack E(X)\rbrack = 0,D\lbrack D(X)\rbrack = 0$

(2) $X$与$Y$相互独立，则$D(X \pm Y) = D(X) + D(Y)$

(3)$\ D\left( C_{1}X + C_{2} \right) = C_{1}^{2}D\left( X \right)$

(4) 一般有 $D(X \pm Y) = D(X) + D(Y) \pm 2Cov(X,Y) = D(X) + D(Y) \pm 2\rho\sqrt{D(X)}\sqrt{D(Y)}$

(5)$\ D\left( X \right) < E\left( X - C \right)^{2},C \neq E\left( X \right)$

(6)$\ D(X) = 0 \Leftrightarrow P\left\{ X = C \right\} = 1$

5.4 随机变量函数的数学期望#

(1) 对于函数$Y = g(x)$

$X$为离散型：$P\{ X = x_{i}\} = p_{i},E(Y) = \sum_{i}^{}{g(x_{i})p_{i}}$；

$X$为连续型：$X\sim f(x),E(Y) = \int_{- \infty}^{+ \infty}{g(x)f(x)dx}$

(2) $Z = g(X,Y)$;$\left( X,Y \right)\sim P\{ X = x_{i},Y = y_{j}\} = p_{{ij}}$; $E(Z) = \sum_{i}^{}{\sum_{j}^{}{g(x_{i},y_{j})p_{{ij}}}}$ $\left( X,Y \right)\sim f(x,y)$;$E(Z) = \int_{- \infty}^{+ \infty}{\int_{- \infty}^{+ \infty}{g(x,y)f(x,y)dxdy}}$

5.5 协方差#

$Cov(X,Y) = E\left\lbrack (X - E(X)(Y - E(Y)) \right\rbrack$

5.6 相关系数#

$\rho_{{XY}} = \frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$,$k$阶原点矩 $E(X^{k})$;
$k$阶中心矩 $E\left\{ {\lbrack X - E(X)\rbrack}^{k} \right\}$

性质：

(1)$\ Cov(X,Y) = Cov(Y,X)$

(2)$\ Cov(aX,bY) = abCov(Y,X)$

(3)$\ Cov(X_{1} + X_{2},Y) = Cov(X_{1},Y) + Cov(X_{2},Y)$

(4)$\ \left| \rho\left( X,Y \right) \right| \leq 1$

(5) $\ \rho\left( X,Y \right) = 1 \Leftrightarrow P\left( Y = aX + b \right) = 1$ ，其中$a > 0$

$\rho\left( X,Y \right) = - 1 \Leftrightarrow P\left( Y = aX + b \right) = 1$
，其中$a < 0$

5.7 重要公式与结论#

(1)$\ D(X) = E(X^{2}) - E^{2}(X)$

(2)$\ Cov(X,Y) = E(XY) - E(X)E(Y)$

(3) $\left| \rho\left( X,Y \right) \right| \leq 1,$且 $\rho\left( X,Y \right) = 1 \Leftrightarrow P\left( Y = aX + b \right) = 1$，其中$a > 0$

$\rho\left( X,Y \right) = - 1 \Leftrightarrow P\left( Y = aX + b \right) = 1$，其中$a < 0$

(4) 下面 5 个条件互为充要条件：

$\rho(X,Y) = 0$ $\Leftrightarrow Cov(X,Y) = 0$ $\Leftrightarrow E(X,Y) = E(X)E(Y)$ $\Leftrightarrow D(X + Y) = D(X) + D(Y)$ $\Leftrightarrow D(X - Y) = D(X) + D(Y)$

注：$X$与$Y$独立为上述 5 个条件中任何一个成立的充分条件，但非必要条件。

6. 数理统计的基本概念

6.1 基本概念#

总体：研究对象的全体，它是一个随机变量，用$X$表示。

个体：组成总体的每个基本元素。

简单随机样本：来自总体$X$的$n$个相互独立且与总体同分布的随机变量$X_{1},X_{2}\cdots,X_{n}$，称为容量为$n$的简单随机样本，简称样本。

统计量：设$X_{1},X_{2}\cdots,X_{n},$是来自总体$X$的一个样本，$g(X_{1},X_{2}\cdots,X_{n})$）是样本的连续函数，且$g()$中不含任何未知参数，则称$g(X_{1},X_{2}\cdots,X_{n})$为统计量。

样本均值：$\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}$

样本方差：$S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{2}$

样本矩：样本$k$阶原点矩：$A_{k} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}^{k},k = 1,2,\cdots$

样本$k$阶中心矩：$B_{k} = \frac{1}{n}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{k},k = 1,2,\cdots$

6.2 常用分布#

$\chi^{2}$分布：$\chi^{2} = X_{1}^{2} + X_{2}^{2} + \cdots + X_{n}^{2}\sim\chi^{2}(n)$，其中$X_{1},X_{2}\cdots,X_{n},$相互独立，且同服从$N(0,1)$

$t$分布：$T = \frac{X}{\sqrt{Y/n}}\sim t(n)$ ，其中$X\sim N\left( 0,1 \right),Y\sim\chi^{2}(n),$且$X$，$Y$ 相互独立。

$F$分布：$F = \frac{X/n_{1}}{Y/n_{2}}\sim F(n_{1},n_{2})$，其中$X\sim\chi^{2}\left( n_{1} \right),Y\sim\chi^{2}(n_{2}),$且$X$，$Y$相互独立。

分位数：若$P(X \leq x_{\alpha}) = \alpha,$则称$x_{\alpha}$为$X$的$\alpha$分位数

6.3 正态总体的常用样本分布#

(1) 设$X_{1},X_{2}\cdots,X_{n}$为来自正态总体$N(\mu,\sigma^{2})$的样本，

$\overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i},S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2},}$则：

1. $\overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right){\ \ }$或者$\frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1)$

2. $\frac{(n - 1)S^{2}}{\sigma^{2}} = \frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2}\sim\chi^{2}(n - 1)}$

3. $\frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \mu)}^{2}\sim\chi^{2}(n)}$

4)${\ \ }\frac{\overline{X} - \mu}{S/\sqrt{n}}\sim t(n - 1)$

6.4 重要公式与结论#

(1) 对于$\chi^{2}\sim\chi^{2}(n)$，有$E(\chi^{2}(n)) = n,D(\chi^{2}(n)) = 2n;$

(2) 对于$T\sim t(n)$，有$E(T) = 0,D(T) = \frac{n}{n - 2}(n > 2)$；

(3) 对于$F\tilde{\ }F(m,n)$，有 $\frac{1}{F}\sim F(n,m),F_{a/2}(m,n) = \frac{1}{F_{1 - a/2}(n,m)};$

(4) 对于任意总体$X$，有 $E(\overline{X}) = E(X),E(S^{2}) = D(X),D(\overline{X}) = \frac{D(X)}{n}$

参考
概率论与数理统计 浙江大学 第4版
概率论辅导讲义 王式安
CS229 - Probability
A First Course in Probability 第9版