高精度计算,又或者说是大数算法,基础思想比较简单,就是用数组的每一个元素来表示每一位,加减注意进位,乘除注意因数的位数,计算原理就是竖式乘除法。
写在前面
本文学习并参考以下两个网站
https://oi-wiki.org/math/bignum/
https://www.cnblogs.com/lfyzoi/p/6737761.html
面对问题为
http://noi.openjudge.cn/ch0106/10/
http://noi.openjudge.cn/ch0106/11/
http://noi.openjudge.cn/ch0106/12/
http://noi.openjudge.cn/ch0106/13/
http://noi.openjudge.cn/ch0106/14/
http://noi.openjudge.cn/ch0106/15/
使用语言为 c
所有因子都是正整数
好,怀着用数组每个元素表示一位的思想来进行大数加减,a+b中a为数组a[]、b为数组b[],此时出现第一个问题,大数的输入和输出(表示)。
先省略一下为什么,大数的输入过程为,先读入为char s[] 字符数组,将字符数组逆序存放并转换为int 数组int a[]。
大数的表示为,a[1] -- a[n] 为数的最低位到最高位,a[1]为第一位等...,这样的好处方便理解,符合数学直觉,a[0]来表示这个数实际有多少位,这样在计算乘除的时候很方便。我将它理解为人类处理问题信息由模糊到计算机处理问题具体、固定化。
大数的输出,a[]逆序输出,开始于a[长度],结束于a[1]。a[长度]== a[a[0]]
讲一下为什么要逆序存放,主要是为了低位在低(小端法),从低位到高位进行计算,方便进位。
简而言之:字符数组读入,逆序(低位在低地址)存入int数组,按自然数索引表示所在哪一位,[0]来存入int数组长度(数的位数)。
1 void getNum(int num[]){ //数组初始化和高精度数字构建 2 char temp[500]; 3 scanf("%s", &temp); //数字作为字符串读入 4 memset(num, 0, sizeof(int)*500); //将数组的所有字节置0 5 num[0]=strlen(temp); //将位数存于num[0]中 6 //strlen memset 在<string.h>中 7 for(int i=1; i<=num[0]; i++) //逆序将每一位存储于num中 8 num[i]=temp[num[0]-i]-'0'; 9 return; 10 } 11 12 //使用方法 13 int main(){ 14 int num1[500]; 15 int num2[500]; 16 getNum(num1); 17 getNum(num2); 18 19 return 0; 20 }
说回scanf("%s",&temp),可读入一个字符串,不包含任何分隔符,可用strlen()来确切表示有效位的位数,由于ascii码和整形int的关系,可以轻松转换。
逆序打印
1 void print(int X[]){ //输出高精度数字 2 for(int i=X[0]; i>=1; i--) printf("%d", X[i]); 3 return; 4 }
高精度加法
大数加法的核心思想就是竖式加法,从低位到高位,每一位相加再加上进位,就能得到结果,C[i]=A[i]+B[i]+jw。注意使用3操作数,来定义void jiafa(int A[], int B[], int C[])
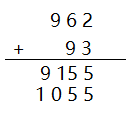
void jiafa(int A[], int B[], int C[]){ //C=A+B int i, jw; //i从1循环至max(A[0], B[0]) for(i=1, jw=0; i<=A[0] || i<=B[0]; i++){ C[i]=A[i]+B[i]+jw; //按位相加 jw=C[i]/10; //求进位 C[i]%=10; //与10求余 } C[i]=jw; //存放最后一个进位,加法的最后一位进位就是1 C[0]=C[i] ? i : i-1; //确定C的位数 return; }
高精度减法
减法思想与加法类似,从低位到高位,每一位相减再减去借位,就能得到结果,注意A要大于B(这样才能一定能借),C[i]=A[i]-B[i]
void sub(int a[], int b[], int c[]) { //c[]一定要全部赋为0,要不然会出奇怪的错误 c=a-b c[0] = a[0]; for (int i = 1; i <= b[0]; ++i) { // 逐位相减,减到b的最高位 c[i] += a[i] - b[i]; if (c[i] < 0) { // 借位 c[i + 1] -= 1; c[i] += 10; } }
i=c[0] while(c[i]==0 &&i>=1) i--; //最高有效位数为a[0],计算第一个不是0的位置 避免减成了1 10000-9999
c[0]=(i==0) ? 1 : i;
return; }
高精度乘法
根据题目的要求,可以分为大数乘数 和 大数乘大数,其核心思想仍然是竖式乘法,借用oi wiki的图,大数乘数
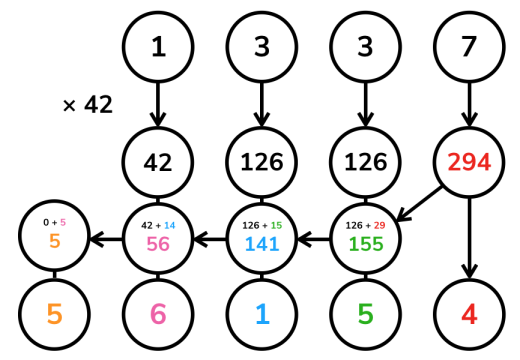
由于int数组每一位能表示,-2^31——2^31-1,即-2147483648——2147483647,可将高精度每一位都乘以低精度,最后再将每一位进位计算,
而进位为 c[i] /10 ,c[i]为c[i] %10
void mul_short(int a[], int b, int c[]) { //c[]一定要全部赋为0 for (int i = 1; i <= a[0]; ++i) { // 直接把 a 的第 i 位数码乘以乘数,加入结果 c[i] += a[i] * b; if (c[i] >= 10) { // 处理进位 // c[i] / 10 即除法的商数成为进位的增量值 c[i + 1] += c[i] / 10; // 而 c[i] % 10 即除法的余数成为在当前位留下的值 c[i] %= 10; } } if(c[i]==0){ //处理位数 c[0] = i-1; } else{ c[0] = i; } return; }
大数乘数实际上就是一种偷懒的方法
大数乘大数,参考lfyzoi,实际上为竖式乘法,a*b ,为b的低位乘一遍a的所有位,到为b的高位乘一遍a的所有位
//array index 1 2 3 4 5 6 7 8 9 ...
A 6 5 8
B 5 2
----------------------------------
0 8 2 4
2 1 7 1
----------------------------------
0 0 4 1 2
//array index 1 2 3 4 5 6 7 8 9 ...
A a1 a2 a3 a4
B b1 b2
----------------------------------
C c1 c2 c3 c4
c2 c3 c4 c5
//本例中未写出进位
综上分析,乘法要进行'b的位数(b[0])'轮,每轮要进行'a的位数(a[0])'次乘法和进位运算,这就找到了循环的规律。结合错位相加,可知c[i+j-1]=c[i+j-1]+a[aj]*b[bi]+jw,进位jw=c[i+j-1]/10
有效位数:计算完成后,需要确定结果的有效位数,使用和减法类似的方法从可能的最大位数往后推,直到遇到非0的数位,当前位置就是有效位数。对于M位的数字A和N位的数字B向乘,最大位数为M+N
void chengfa(int A[], int B[], int C[]){ //C=A*B int i,j; for(i=1; i<=B[0]; i++){ //B[0]轮乘法 int jw; //进位 for(j=1, jw=0; j<=A[0]; j++){ //每轮按位乘A[0]次 C[i+j-1]=C[i+j-1]+A[j]*B[i]+jw; //错位相加 jw=C[i+j-1]/10; //求进位 C[i+j-1]%=10; //进位后,与10求余 } C[i+A[0]]=jw; //存储最后一个进位 } int len=A[0]+B[0]; //最大可能位数 while(C[len]==0 && len>1) len--; //确定有效位数 C[0]=len; return; } //使用方法 int main(){ ... chengfa(num1, num2, result); printNum(result); return 0; }
高精度除法
以下内容完全参考fyzoi,完全照抄
思路
高精度初低精度采用竖式思想,由于除数是低精度,最后的商可能是高精度,余数一定为低精度。
商有效位数:M位的数字A除以N位的数字B,商的位数最大为M-N+1,因为B是低精度数字,计算长度N比较麻烦,简单起见,也可以认为商的最大位数为M, 从最大数位往后推,直到遇到非0的数位,当前位置就是有效位数。
以下是一个模拟计算过程的例子,113056/23:
// 被除数数位 当前位数字 过程被除数 过程除结果 i=6 1 1/23 商:0 i=5 1 11/23 商:0 i=4 3 113/23 商:4,余:21 i=3 0 210/23 商:9,余:3 i=2 5 35/23 商:1,余:12 i=1 6 126/23 商:5,余:11 //计算结果 商:4915, 余数:11
代码 针对c修改了一下(可能用指针改变更小)
int chuDi(int A[], int B, int C[]){ //A/B=C 返回余数:yushu int i, t,yushu; //t为过程被除数 for(i=A[0], t=0; i>=1; i--){ //从被除数高位循环到低位 t=t*10+A[i]; //更新t C[i]=t/B; //计算C[i] t%=B; //更新t } yushu=t; //计算完后t就是余数 i=A[0]; //计算C有效位数 while(C[i]==0 && i>1) i--; C[0]=i; return yushu; } //使用方法 int main(){ int num1[500]; int num2; int shang[500]; int yushu; getNum(num1); scanf("%d", num2); yushu=chuDi(num1, num2, shang); printNum(shang); printf(" %d",yushu); return 0; }
高精度除高精度
思路
高精度除高精度是这几种运算中最难的一种。仍然可以模仿竖式的方式进行,过程有点儿麻烦。另一种办法是利用减法:被除数A-除数B,看看能减多少个,直到A<B,这时剪去的个数就是商,剩下的A就是余数。如果利用前面编写好的高精度减法jianfa()和compare()的话,实现起来岂不是很容易?可惜不是这样,假设被除数A的位数M与除数B位数N之差M-N很大,这个范围有可能从0~200,按照最大的情况200考虑,这意味着商值也是高精度数字,而你要减10^200次才能减完,这是一个天文数字。
所以,明白否?解决这个问题也很简单,我们不一个一个减,而是按照最大可能的数量级减,例如:12345/45:
//商的最大位数i=M-N+1,即4,设计一个 临时减数,减数后面补齐i-1个0,再进行减法 i=4 12345 < 45000 可以减0个 shang[4]=0 减后A:12345 i=3 12345 < 4500 可以减2个 shang[3]=2 减后A:3345 i=2 3345 < 450 可以减7个 shang[2]=7 减后A:195 i=1 195 < 45 可以减4个 shang[1]=4 减后A:15 //因shang[4]=0,故商的有效位数shang[0]--,为3 //结果 商为274,余数15
这样的计算过程,仅仅减了2+7+4=13次,而非274次,可见一个一个减是绝对不靠谱的。下面提供了代码,注意:减法函数jianfa()被修改了,使得直接把结果存入A中,而不需要存在另一个数组C中,这是为了简化后面运算的缘故。
代码
void jianfa(int A[], int B[]){ //修改了的减法,使得直接在A数组上减 int i; //不再需要存在数组C,简化后面的运算 for(i=1; i<=B[0]; i++){ if(A[i]<B[i]){ A[i+1]--; //向高位借1 A[i]+=10; //当前位+10 } A[i]-=B[i]; //按位减 } if(i<A[0]) return; //计算有效位数 else{ while(A[i]==0 && i>=1) i--; A[0]=(i==0)? 1 : i; } return; } //shang=A/B, yushu为余数 bool chuGao(int A[], int B[], int shang[], int yushu[]){ memset(shang, 0, sizeof(int)*300); //初始化shang memset(yushu, 0, sizeof(int)*300); //初始化yushu shang[0]=A[0]-B[0]+1; //商的最大数位 for(int i=shang[0]; i>=1; i--){ //从高位到低位开始计算商 int jianshu[300]; //构造要减的减数 memset(jianshu, 0, sizeof(jianshu)); //这个函数下面有解释 memcpy(jianshu+i, B+1, sizeof(int)*B[0]); jianshu[0]=B[0]+i-1; //确定减数的位数 while(compare(A, jianshu)){ //通过循环减 jian(A, jianshu); shang[i]++; //减去一个商的对应为+1 } } if(shang[shang[0]]==0) shang[0]--; //判断商的最高位是否有效 memcpy(yushu, A, sizeof(int)*300); //A就是余数,把它完全复制给yushu } //使用方法 int main(){ int num1[300]; //数组A存储第1个数字信息 int num2[300]; //数组B存储第2个数字信息 int shang[300]; int yushu[300]; init(num1); init(num2); chuGao(num1, num2, shang, yushu); print(shang); printf(" "); print(yushu); return 0; }
原理都讲完了,在具体题上每个都不太一样,可以按照高精度计算的思想,但代码是简化的
10:大整数加法 http://noi.openjudge.cn/ch0106/10/
按照oiwiki,基本上不需要修改,比较简单也就不用费力计算位长,代码ac
//完全按照oiwiki,[0]不是位数长度,位长用从数组最后一位一直到首个非零数 #include<stdio.h> #include<string.h> #define LEN 201 int a[LEN],b[LEN],c[LEN]; void clear(int a[]){ int i; for(i=0;i<LEN;i++){ a[i] = 0; } } void read(int a[]){ char s[LEN+1]; int len,i; scanf("%s",s); clear(a); len = strlen(s); for(i=0;i<len;i++){ a[len-i-1] = s[i] - '0'; } } void print(int a[]){ int i; for(i = LEN-1;i>=1;--i){ if(a[i]!=0){break;} } for(;i>=0;i--){ printf("%c",a[i]+'0'); } printf("\n"); } void add(int a[],int b[], int c[]){ clear(c); for(int i=0;i<LEN-1;++i){ c[i] += a[i] + b[i]; if(c[i]>=10){ c[i+1] +=1; c[i] -=10; } } } int main(){ read(a); read(b); add(a,b,c); print(c); return 0; }
11:大整数减法 http://noi.openjudge.cn/ch0106/11/
完全按照oiwiki,代码ac
#include<stdio.h> #include<string.h> #define LEN 201 int a[LEN],b[LEN],c[LEN]; void clear(int a[]){ int i; for(i=0;i<LEN;i++){ a[i] = 0; } } void read(int a[]){ char s[LEN+1]; int len,i; scanf("%s",s); clear(a); len = strlen(s); for(i=0;i<len;i++){ a[len-i-1] = s[i] - '0'; } } void print(int a[]){ int i; for(i = LEN-1;i>=1;--i){ if(a[i]!=0){break;} } for(;i>=0;i--){ printf("%c",a[i]+'0'); } printf("\n"); } void add(int a[],int b[], int c[]){ int i; clear(c); for(i=0;i<LEN-1;++i){ c[i] += a[i] + b[i]; if(c[i]>=10){ c[i+1] +=1; c[i] -=10; } } } void sub(int a[],int b[],int c[]){ int i; clear(c); for(i=0;i<LEN-1;i++){ c[i] += a[i]-b[i]; if(c[i]<0){ c[i+1] -=1; c[i] += 10; } } } int main(){ read(a); read(b); sub(a,b,c); print(c); return 0; }
12:计算2的N次方 http://noi.openjudge.cn/ch0106/12/
完全按照oiwiki的思想,2的N次方为大数乘数,每次先进行乘法,再进行进位。比较蠢的地方每次都是整个长度的遍历,处于优化遍历长度想法,之后才学习了lfyzoi的题解,代码ac
#include<stdio.h> int main(){ int s[101],n,i,k,t; scanf("%d",&n); for(i=0;i<101;i++){ s[i] = 0; } s[0] = 1; for(i=0;i<n;i++){ for(k=0;k<101;k++){ s[k] *=2; } for(k=0;k<101;k++){ if(s[k]>=10){ s[k+1] += s[k]/10; s[k] = s[k]%10; } } } for(i = 100;i>=1;--i){ if(s[i]!=0){break;} } for(;i>=0;i--){ printf("%d",s[i]); } printf("\n"); return 0; }
13:大整数的因子 http://noi.openjudge.cn/ch0106/13/
按照lfyzoi高精度除以低精度来进行计算,由于除的数是仅是2-9,也懒得用数学方法来判断是否能出尽(比如mod2==0 要求24680,mod3==0 要求每位和 mod3==0,mod4==0要求mod两次2,mod5==0则为位数为0、5,mod6 ==0同时满足mod2==0、mod3==0,mod7只好除了,mod8除4看能否mod2,mod9为除3后mod3),不如写好chuDi然后循环就行了
代码ac
#include<stdio.h> #include<stdlib.h> #include<string.h> #define LEN 200 void getNum(int num[]){ char temp[LEN]; scanf("%s",&temp); memset(num,0,sizeof(int)*LEN); num[0] = strlen(temp); //printf("%d\n",num[0]); for(int i=1; i<=num[0];i++){ num[i] = temp[num[0]-i] - '0'; //printf("%d ",num[i]); } return; } int chuDi(int a[], int b, int c[], int yushu){ int i,t; for(i = a[0], t = 0; i>=1; i--){ t = t*10 + a[i]; c[i] = t/b; t %= b; //printf("%d:%d:%d:%d ",a[i],b,c[i],t); } yushu = t; i = a[0]; while(c[i]==0 && i>1){ i--; } c[0] = i; return yushu ; } int main(){ int i,count=0; int num1[LEN]; int num2[8]={2,3,4,5,6,7,8,9}; int shang[LEN]; int yushu; getNum(num1); for(i=0;i<8;i++){ yushu=chuDi(num1,num2[i],shang,yushu); if(yushu==0){ printf("%d ",num2[i]); count++; } } if(count==0){ printf("none"); } return 0; }
14:求10000以内n的阶乘 http://noi.openjudge.cn/ch0106/14/
阶乘核心仍然是一个chengDi(int a[],int b, int c[]),我为了便于循环,在chengDi内把c又赋值给了a(可能比较蠢),这里把a[0]处理成了位长便于直观化思考,而且不假思索的从最长开始计算,浪费了不少计算,可设计动态计算位数,代码提交后几乎就要超时了优化空间应该还有不少,毕竟很多提交的代码时间也就是我的一半,代码ac
#include<stdio.h> #include<stdlib.h> #include<string.h> #define LEN 35662 //10000!有35660位 void print(int x[]){ int i; for(i =x[0];i>=1;i--){ printf("%d",x[i]); } //printf("\n"); return ; } void chengDi(int a[],int b, int c[]){ int i; memset(c,0,sizeof(int)*LEN); for(i=1;i<=LEN-1;i++){ c[i] += a[i] * b; if(c[i] >= 10){ c[i+1] += c[i] /10; c[i] %= 10; } } for(i = LEN -1; i>=1;--i){ //printf("-%d:%d ",i,c[i]); if(c[i] !=0){break;} } c[0] = i; //printf("%d ",i); a[0] = c[0]; for(i=1;i<=a[0];i++){ a[i] = c[i]; } return; } int main(){ int n,i; int num1[LEN]; int result[LEN]; memset(num1,0,sizeof(int)*LEN); memset(result,0,sizeof(int)*LEN); num1[1] = 1; //1的高精度表示 num1[0] = 1; //位数 scanf("%d",&n); // printf("%d",n); if(n==0){ printf("1"); } for(i = 1; i<=n;i++){ chengDi(num1,i,result); //print(result); } print(result); return 0; }
15:阶乘和 http://noi.openjudge.cn/ch0106/15/
阶乘和思路和求阶乘一样,只不过是多了个大数加法,而且我为了图好循环,在加法和乘法内都把c赋值给了a,而且为了偷懒计算又一次从数组最后一位开始计算了
,丝毫没有管 m位*n位不大于max(m位+n位),搞定了14,15就简单多了,代码ac
#include<stdio.h> #include<stdlib.h> #include<string.h> #define LEN 100 void print(int x[]){ int i; for(i =x[0];i>=1;i--){ printf("%d",x[i]); } //printf("\n"); return ; } void jiafa(int a[], int b[]){ int i, jw; //两数相加最大位数是max(a[0],b[0])+1 int c[LEN]; memset(c,0,sizeof(int)*LEN); for(i=1,jw=0; i<a[0]||i<=b[0]; i++){ c[i] = a[i] + b[i] +jw; jw = c[i]/10; c[i] %= 10; } c[i] = jw; //存最后一个进位 c[0] = c[i] ? i : i-1; a[0] = c[0]; for(i=1;i<=a[0];i++){ a[i] = c[i]; } return; } void chengDi(int a[],int b){ int i; int c[LEN]; memset(c,0,sizeof(int)*LEN); for(i=1;i<=LEN-1;i++){ c[i] += a[i] * b; if(c[i] >= 10){ c[i+1] += c[i] /10; c[i] %= 10; } } for(i = LEN -1; i>=1;--i){ //printf("-%d:%d ",i,c[i]); if(c[i] !=0){break;} } c[0] = i; //printf("%d ",i); a[0] = c[0]; for(i=1;i<=a[0];i++){ a[i] = c[i]; } return; } int main(){ int n,i; int num1[LEN],sum[LEN]; memset(num1,0,sizeof(int)*LEN); memset(sum,0,sizeof(int)*LEN); num1[1] = 1; //1的高精度表示 num1[0] = 1; //位数 scanf("%d",&n); // printf("%d",n); if(n==0){ printf("1"); } for(i = 1; i<=n;i++){ chengDi(num1,i); //print(result); jiafa(sum,num1); } print(sum); return 0; }
写到最后
搞了一天的大数计算,虽然ac了,总结的时候也发现还能优化一下。核心代码就那几句,反而为了完成问题,写的很复杂。网上参考的代码还是需要自己测试一遍才能使用,熟练掌握printf测试方法,而且搞清楚原理后再开始计算,这样更好,还有感叹好的数据结构和能使算法具体实现简单很多。
还有计算阶乘参考两个 1)10000! 有 35660 位数,而不是开一个10000大小的数组2)网上找好阶乘表,能快速查到错误的地方。我出错的地方总是循环上限没好好控制,出现了某一位超出int的尴尬情况,于是就是索性从数组最高位开始计算。
最后的最后
本文参考于
https://oi-wiki.org/math/bignum/
https://www.cnblogs.com/lfyzoi/p/6737761.html
http://www.ab126.com/xuexi/2016-10-16/3730.html
如有雷同,不是意外



