数据结构-kmp算法
定义 改进字符串的匹配算法
关键:通过实现一个包含了模式串的局部匹配信息的next()函数,利用匹配失败的信息,减少匹配次数。
1.BF算法 暴力匹配
给定 文本串S “BBC ABCDAB ABCDABCDABDE” 存储为 s[i] 和模式串 P “ABCDABD” 存储为p[j] 进行匹配
思路
p串与S串逐一匹配 ,不匹配则 p串右移一位,匹配下一个 。


p串不断右移 直到第四位匹配成功


不断向后匹配 直到失败

i,j回退到p串在s串的初始位置,p串右移匹配下一位。

暴力代码:
int ViolentMatch(char* s, char* p)
{
int sLen = strlen(s);
int pLen = strlen(p);
int i = 0;
int j = 0;
while (i < sLen && j < pLen){
if (s[i] == p[j]){ //①如果当前字符匹配成功(即S[i] == P[j]),则i++,j++
i++;
j++;
}
else{// ②如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0
i = i - j + 1;
j = 0;
}
}
if (j == pLen)//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
return i - j;
else
return -1;
}
2. kmp算法 优化匹配(利用next() 优化)
KMP算法和BF算法的“开局”是一样的,同样是把主串和模式串的首位对齐,从左到右对逐个字符进行比较。
第一轮,模式串和主串的第一个等长子串比较,发现前5个字符都是匹配的,第6个字符不匹配,是一个“坏字符”:
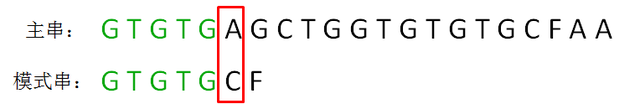
这时候,如何有效利用已匹配的串 “GTGTG” 呢?
我们可以发现,在串GTGTG”当中,后三个字符“GTG”和前三位字符“GTG”是相同的:

在下一轮的比较时,把这两个相同的片段对齐,出现匹配。 GTG 是串GTGTG 前缀后缀公共元素中最长的
第二轮,我们直接把模式串向后移动两位,让两个“GTG”对齐,继续从刚才主串的坏字符A开始进行比较:
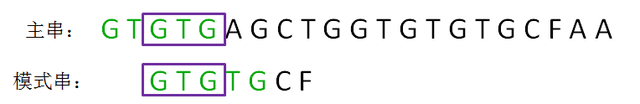
显然,主串的字符A仍然是坏字符,这时候已经匹配的串缩短成了GTG:
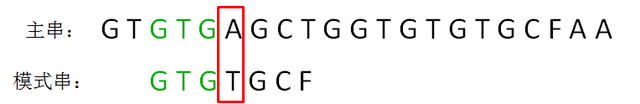
按照第一轮的思路,我们来重新确定 前缀后缀最长公共元素:

第三轮,我们再次把模式串向后移动两位,让两个“G”对齐,继续从刚才主串的坏字符A开始进行比较:
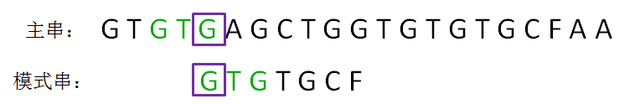
以上就是KMP算法的整体思路:在已匹配的串当中寻找到 前缀后缀最长公共元素,在下一轮直接把两者对齐,从而实现模式串的快速移动。
3.求出next()函数的方式
①寻找前缀后缀最长公共元素长度
基本概念:
字符串abcda为例子
前缀 : 最后一个字符以外,一个字符串的全部头部组合。 例子abcda的前缀为 a ab abc abcd
后缀 : 第一个字符以外,一个字符串的全部尾部组合。 例子abcd的后缀为 bcda cda da a
前缀后缀最长公共元素 : 前缀后缀相同的元素,且长度最长的一个。例子的共同元素为a 长度为1
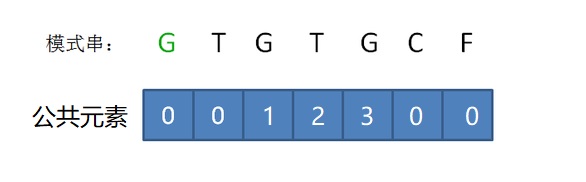
给定一个模式串 GTGTGCF
G无前缀后缀 公共元素长度为0
GT 前缀 G 后缀T公共元素长度为0
GTG 前缀G GT 后缀 TG G 公共元素G 长度为1
GTGT前缀 G GT GTG 后缀 TGT GT G 公共元素 GT 长度为 2
GTGTG 前缀G GT GTG GTGT 后缀 TGTG GTG TG G 公共元素GTG 长度为3
GTGTGC 前缀G GT GTG GTGT GTGTG 后缀 TGTGC GTGC TGC GC C 公共元素长度为0
GTGTGCF 前缀G GT GTG GTGT GTGTG GTGTGC 后缀 TGTGCF GTGCF TGCF GCF CF公共元素长度为0
得到串的 前缀后缀最长公共元素长度 如表
各个子串的最后一位对应该串的 最长公共元素长度
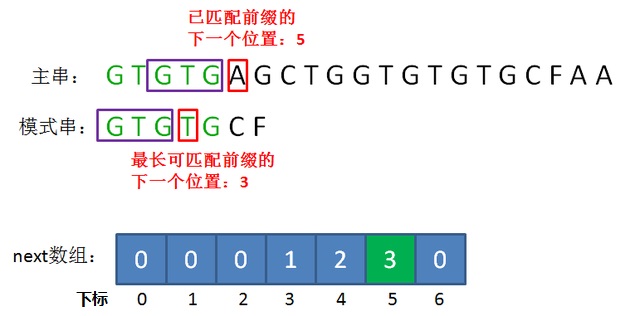
②求next数组
next数组 是一维整型数组,数组的下标代表了“已匹配串的长度 也是 已匹配串的下一位置 ”,
元素的值则是“ 已匹配串 前缀后缀最长公共元素 的长度 也是 已匹配串 前缀后缀最长公共元素 的下一个位置”。
通过next数组即可将公共元素部分对齐
void GetNext(char* p,int next[]) { int pLen = strlen(p); next[0] = 0; int k = -1; int j = 0; while (j < pLen - 1) { //p[k]表示前缀,p[j]表示后缀 if (k == -1 || p[j] == p[k]) { ++k; ++j; next[j] = k; } else { k = next[k]; } } }
代码
int KmpSearch(char* s, char* p)
{
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen)
{
//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
4 kmp对next()的进一步优化
扩展算法
1.BM算法
2 study算法


