dfs序

DFS序：

每个节点在dfs遍历中进出栈的时间序列

将树形结构转化为线性结构，用dfs遍历一遍这棵树，进入到x节点有一个in时间戳，递归退出时有一个out时间戳，

x节点的两个时间戳之间遍历到的点，就是根为x的子树的所有节点。

 

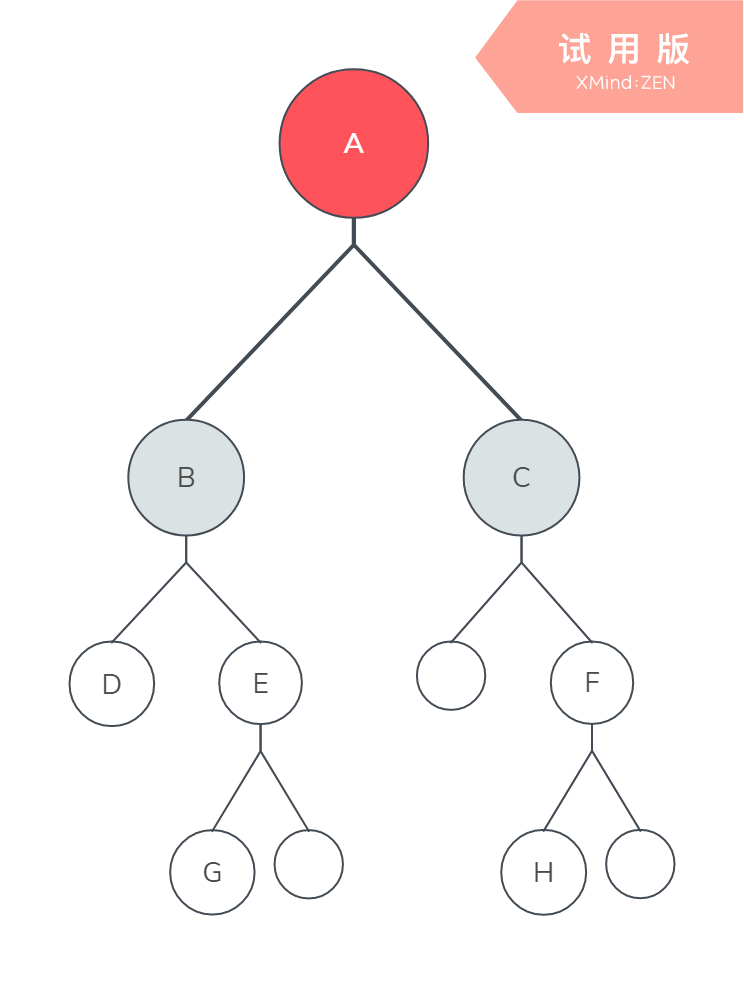
dfs序就是A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A 

void dfs(int node,int parent){
    NewIdx[NCnt] = node;
    InOut[NCnt] = 1;
    InIdx[node] = NCnt++;
    for(int next=Vertex[node];next;next=Edge[next].next){
        int son = Edge[next].to;
        if ( son != parent ) dfs(son,node);
    }
    NewIdx[NCnt] = node;
    InOut[NCnt] = -1;
    OutIdx[node] = NCnt++;
}

dfs序求lca

       点u,v的LCA还满足 它是其中一个点的最近的一个祖先，满足u,v都在它的子树中。

　　判断一个点是否在另一个点的子树中，我们可以用dfs序来判断。

　　这是倍增的另一种判断方法：

void dfs(int p, int fa) {
      bz[p][0] = fa, in[p] = ++cnt;
      for (int i = 1; i < bzmax; i++)
          bz[p][i] = bz[bz[p][i - 1]][i - 1];
      for (int i = g.h[p]; ~i; i = g[i].nx) {
          int e = g[i].ed;
          if (e == fa)    continue;
          dfs(e, p);
      }
     out[p] = cnt;
 }
  
 int lca(int a, int b) {
     if (dep[a] > dep[b])    swap(a, b);
     if (in[a] <= in[b] && out[a] >= out[b])
         return a;
     for (int i = bzmax - 1, nx; ~i; i--) {
         nx = bz[a][i];
         if (!(in[nx] <= in[b] && out[nx] >= out[b]))
             a = nx;
     }
     return bz[a][0];

 

参考博客：https://www.cnblogs.com/kousak/p/9192094.html