求逆序对

逆序对的定义：

在一个数列aa中，满足a[i]>a[j]a[i]>a[j]并且i<ji<j的数对就叫做逆序对。

解法：

一般有两种解法：归并排序和树状数组。

归并排序动图：

 

 

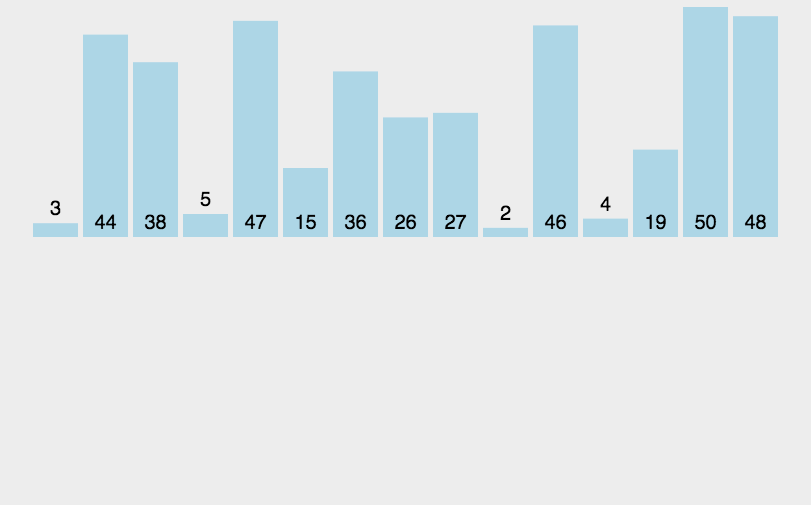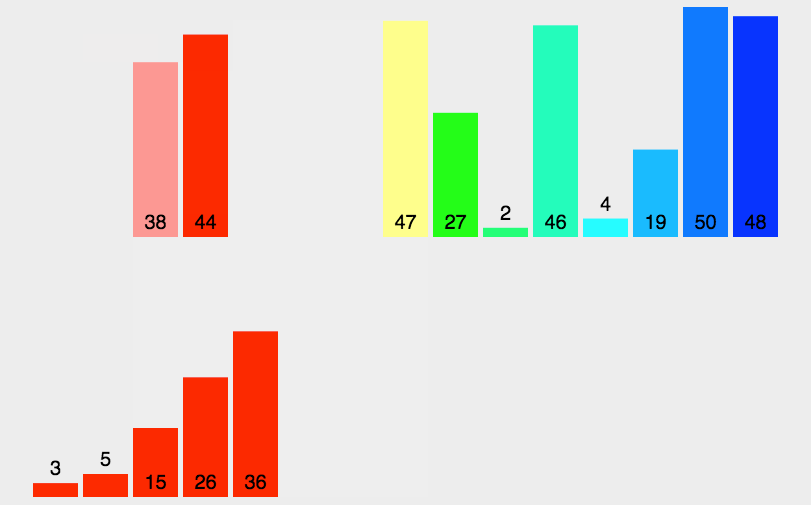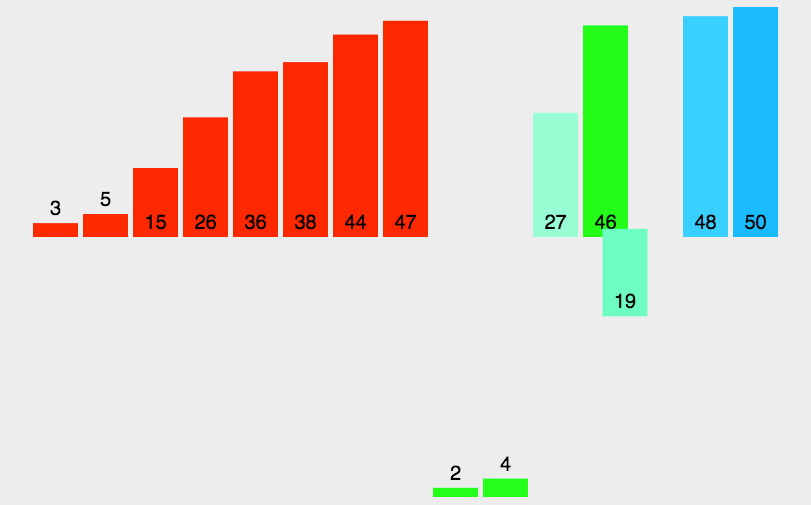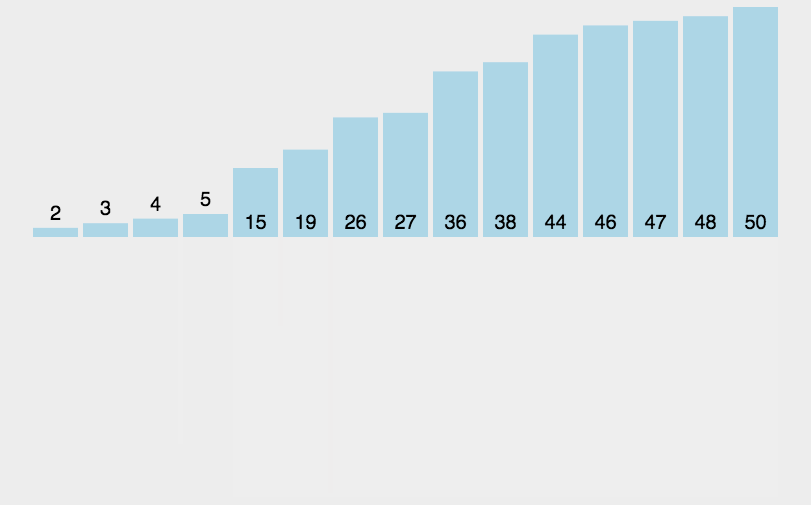
归并求逆序对：

归并排序用到了二分的思想，在排序过程中如果a[i]<=a[j] 就不会产生逆序对，如果a[i]>a[j]就会产生mid−i+1个逆序对，

因为做归排的时候l～mid和mid+1～r都是已经排好序的所以如果a[i]>a[j]那么a[i+1]～a[mid]也就都大于a[j]。

#include<cstdio>
#include<algorithm>
#define maxn 1000
using namespace std;
int n,A[maxn],temp[maxn],ans;
void merge(int L1,int R1,int L2,int R2)
{
    int k=0,i=L1,j=L2;
    while(i<=R1 && j<=R2)
    {
        if(A[i]<=A[j]) temp[k++]=A[i++];
        else if(A[i]>A[j])
        {
            ans+=(R1-i+1);
            temp[k++]=A[j++];
        }
    }
    while(i<=R1) temp[k++]=A[i++];
    while(j<=R2) temp[k++]=A[j++];
    for(i=0;i<k;i++) A[L1+i]=temp[i];
}
void mergeSort(int L,int R)
{
    if(L<R)
    {
        int mid = (L+R)/2;
        mergeSort(L,mid);
        mergeSort(mid+1,R);
        merge(L,mid,mid+1,R);
    }
}
int main(void)
{
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&A[i]);
    mergeSort(0,n-1);
    printf("%d",ans);
    return 0;
}

 

树状数组：

1.能够查询某段区间的和；2.能够随时更新某个数的值。

使用函数int sum(int k)计算a[1]+a[2]+...+a[k]的值。

使用函数update(int k,int change)更新所有包含a[x]的t[i],让t[i]+=change;

使用树状数组求逆序对可能还需要进行离散化操作（因为数据过大的话无法直接开数组），

对于离散后的序列进行一次遍历，遍历过程中就向树状数组C进行插入操作（每次插入的值为1），

这里树状数组表示的是在该元素前面但是比该元素大的元素个数，进行插入操作以后就查询。

#include<cstdio>
#define maxn 100010
int n,a[maxn],t[maxn],ans;
int sum(int k)
{
    int s = 0;
    for(int i=k;i>0;i-=i&(-i)) s+=t[i];//所求的区间长度和 = 当前管线的区间和 + 剩下的区间长度和
    return s;
}
void update(int k,int change)
{
    for(int i=k;i<=n;i+=i&(-i)) t[i]+=change;//每一次循环就是找到了下一个包含k的区间对应的t[i]
}
int main(void)
{
    int num;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&num);
        a[num]++;
        update(num,1);
        ans+=i-sum(num);//sum(num)计算的是小于等于num的总数，当前总数i-sum(num)大于num的元素的个数，就是逆序的个数。
    } 
    printf("%d",ans);
    return 0;
}