树状数组

树状数组定义：

是一个查询和修改复杂度都为log(n)的数据结构。可以用于处理前缀和的问题,动态维护前缀和的工具

区间修改和区间查询用树状数组会显得很麻烦 相对而言用线段树会更灵活。

基本操作：求数列区间和，可以对数列单点进行操作。

前置知识：

差分数组

lowbit（）操作：返回非负整数x 在二进制表示下，第一个1和后面的0表示的数值（十进制的值）。

int lowbit(int x)
{
     return x&(-x);
}
/*
-i 代表i的负数 计算机中负数使用对应的正数的补码来表示
k表示i的二进制中末尾连续0的个数。
例如 : i=6（0110） 此时 k=1
-i=-6=(1001+1)=(1010)
 i&(-i)=(0010)=2=2^K k=1.
C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i];
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i];
*/

树状数组思想：

区间查询——》前缀和  ——》树结构维护（log₂n）

树状数组 t[x] 保存以x为根的子树中叶节值的和 。

观察 t[x] 中每个x的二进制，每一层末尾零相同 ，零的个数即K对应覆盖的长度，覆盖长度就是lowbit（x）。

 t [x] 的父节点为 t【x+lowbit[x]】 树的深度为 log₂n+1

 

 

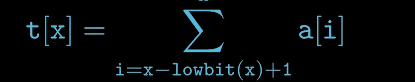
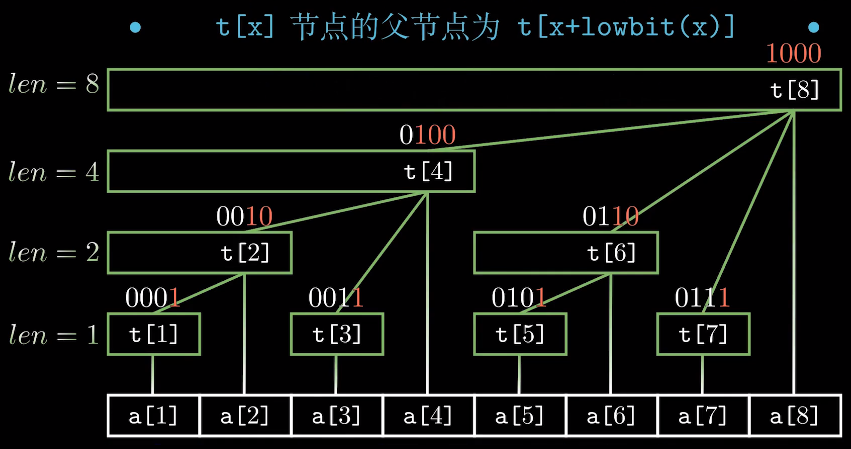
基本操作（单点修改 查询前缀和）

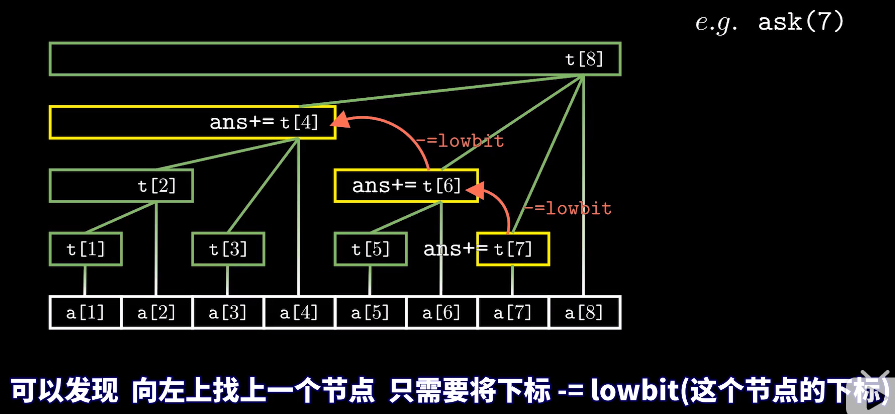
void update(int i,int val)//单点更新
{
    while(i<=n){
        t[i]+=val;
        i+=lowbit(i);//由叶子节点向上更新树状数组C，从左往右更新
    }
}
int ask(int x)//求区间[1,i]内所有元素的和 即求前缀和
{
    int ans=0;
    while(x>0){
        ans+=t[x];//从右往左累加求和
        x-=lowbit(x);
    }
    return ans;
}

   

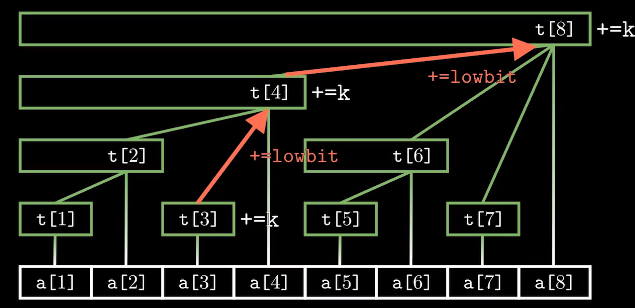
树状数组初始化

memset(a, 0, sizeof a);
memset(c, 0, sizeof c);

cin>>n;

for(int i = 1; i <= n; i++){

 　　cin>>a[i];

 　　updata(i,a[i]); //输入初值的时候，也相当于更新了值

 }

 

 树状数组的用法

1.单点修改，单点查询    update（x,val) ;  ask(x) - ask(x-1);

2.单点修改，区间查询     update（x,val) ;  ask(r) - ask(l-1);

3.区间修改，单点查询  （差分数组 ） 

　用树状数组维护差分数组的前缀和，即原数列的每个元素,由于区间修改 ，产生的改变量。

　区间修改 [l,r]+d    update（l,d)   update(r+1,-d)　

　查询 a[x]                ans =a[x]+ask(X)　

4. 区间修改，区间查询 

 　　求出原数列a[x]的前缀和  ans=a[r]-a[l]   原数列的前缀和也可以用差分数组来求 

 

 

 

 参考