深度哈希检索代码解读之DSH(Deep Supervised Hashing for Fast Image Retrieval)
DSH(CVPR2016)
论文链接： Deep Supervised Hashing for Fast Image Retrieval
github上有人实现了这篇论文的代码： DSH-pytorch，我结合其他深度哈希检索的算法做了一个baseline的汇总，其中DSH代码的链接：https://github.com/swuxyj/DeepHash-pytorch/blob/master/DSH.py
基本背景
深度哈希检索的目标是学习出一个深度神经网络模型。输入图片，这个模型可以将这个图片转换成“01010101111”这样的二进制编码，转换后，图像之间的语义相似性能够通过哈希编码的相似度来体现。比如左图自由女神像和中间的拿破仑图像的语义相似性很小，因此得到的哈希编码的相似度就很小；中间的拿破仑和右边的拿破仑图像语义很接近，因此得到的哈希编码相似度很大。
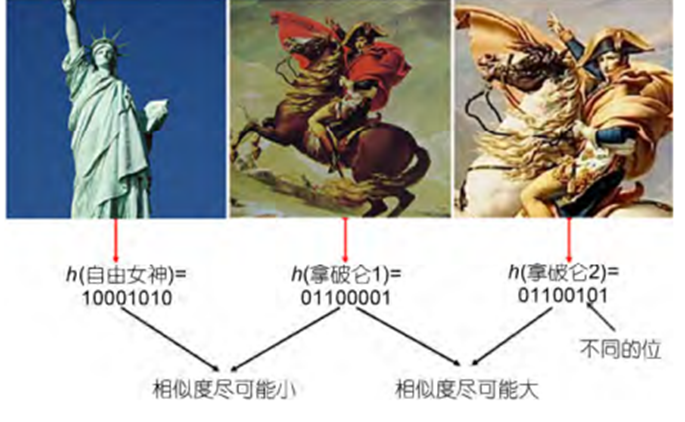
哈希编码的相似度可以使用汉明距离，汉明距离是两个相同长度的编码对应位不同的数量，比如1011101 与 1001001 之间的汉明距离是 2，因为有两位不一样。如果将编码使用+1，-1来进行表示，那么汉明距离和内积有一个关系：
$D_h(b_1,b_2)=(K-b_1^Tb_2)/2$
其中K表示编码长度。显然当$b_1,b_2$每一位都相等的话，$b_1^Tb_2$的内积为$K$。每有一位不同，内积就会少2，因此有这样一个对应关系。
哈希编码的好处是时间复杂度和空间复杂度都很小，比如，用512个浮点数表示图片，和用48个二进制编码表示图片比起来，当然512位浮点数检索的时候计算起来的开销就很大，存储的开销也很大。
总体说来深度哈希检索的目标就是让相似的图片特征之间尽可能近，不相似的图片特征之间尽可能远。当然哈希编码不一定是针对图片的，也有论文针对视频音频来编码。相似不相似由标签信息得到，特征则由图片输入进深度神经网络来得到，最后特征之间的近和远可以使用余弦相似度、欧氏距离、汉明距离这些来进行衡量。
算法框架
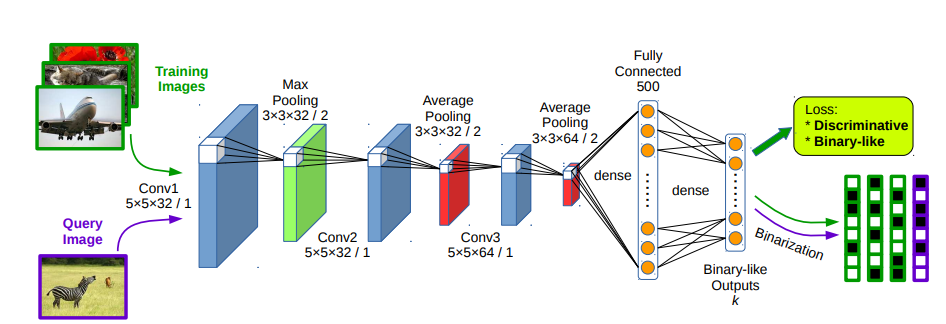
DSH算法的结构如上图所示，输入图片，通过卷积神经网络，最后得到一个k维的输出，用这个输出计算loss，通过loss方向传播计算梯度，从而更新网络的参数。中间的网络是作者自定义的一个网络结构，为了公平的作为baseline，我在实践的时候统一使用了AlexNet作为baseline。
对于图片$x_1,x_2$，数据集给定了它们的相似性y，如果y=0表示它们相似，y=1表示它们不相似。图片$x_1,x_2$通过卷积神经网络后，变成了$b_1,b_2$。分两种情况讨论：
- 当y=0时，图片$x_1,x_2$相似，这个时候$b_1,b_2$之间的汉明距离$D_h(b_1,b_2)$越大，模型的误差就越大，因此损失为
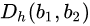; - 当y=1的时候，图片$x_1,x_2$不相似，这个时候$b_1,b_2$之间的汉明距离$D_h(b_1,b_2)$越小，模型的误差就越大，作者希望模型的汉明距离大于m，大于m的话误差为0，小于m的话误差就是$m-D_h(b_1,b_2)$，可以使用max函数来表示这一想法，即$max(m-D_h(b_1,b_2),0)$
将两种情况汇总就能得到如下损失函数：
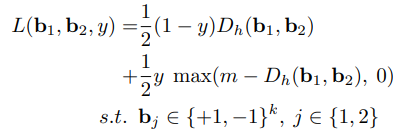
松弛操作
现在的存在一个问题，神经网络的输出是连续的实数而不是+1，-1这样离散的两个值，因此需要做一个松弛操作，即将汉明距离改成欧氏距离，再加上一个对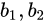
的L1正则化，因此最终的损失函数如下图所示：
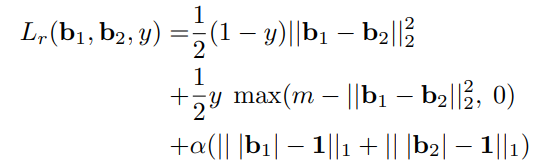
这里的alpha就是一个超参数，需要调整的，我在实践中发现取0.1的时候效果最好。
代码部分
代码的其他部分，如计算MAP，用dataloader加载数据等部分和其他的深度哈希检索算法都基本一致，因此本篇博客主要讲解损失函数计算部分。
训练的时候使用了非对称的思想，有点类似与ADSH那篇文章。
假定batch size=64, 编码长度bit=12，训练集中共有10500张图片，那么卷积神经网络的输出
的shape就是$64\times12$，训练集U的shape是10500x12，表示训练集中所有图片的特征。论文中的损失公式是要计算两张图片特征的欧氏距离，首先需要两个特征相减，然后平方求和，最后开根号，公式后面有一个平方，因此就不用开根号了，具体如下，推导如下所示：
$||b_1 - b_2||_2^2=(b_1^{(0)}-b_2^{(0)})^2+(b_1^{(1)}-b_2^{(1)})^2+……+(b_1^{(11)}-b_2^{(11)})^2$
$64\times12$的u和$10500\times12$的U要相减需要先改变它们的维度，再利用pytorch的广播机制进行相减，u.unsqueeze(1)的shape是$64\times 1 \times 12$，U.unsqueeze(0)的shape是$1 \times 10500 \times12$，进行相减后u.unsqueeze(1) - self.U.unsqueeze(0)的shape是$64 \times 10500 \times12$，此时计算dist = (u.unsqueeze(1) - self.U.unsqueeze(0)).pow(2).sum(dim=2)就可以求的欧氏距离^2。
如果有公共的标签就算做相似，记作y=1。 这里的标签形如 [1 1 0 0 0 1]，表示该图片属于第0类、第1类和第5类，假定另外一张图片的标签是[1 0 0 0 0 0]，让[1 1 0 0 0 1]和[1 0 0 0 0 0]计算内积，得到$1\times1+1\times0+0\times0+0\times0+0\times0+1\times0=1$，是大于0的，表明有是相似的，y应该为0。只要计算内积再判断是否大于0，就能判断两张图片是否是相似的，从而得到y值。论文中的y可以通过代码： (y @ self.Y.t() == 0).float()进行计算。
这篇论文公式最难计算的部分就是上面欧氏距离的计算和y的计算，其他部分和其他深度检索的代码都差不多，具体的损失函数代码计算如下：
class DSHLoss(torch.nn.Module): def __init__(self, config, bit): super(DSHLoss, self).__init__() self.m = 2 * bit self.U = torch.zeros(config["num_train"], bit).float().to(config["device"]) self.Y = torch.zeros(config["num_train"], config["n_class"]).float().to(config["device"])
def forward(self, u, y, ind, config): self.U[ind, :] = u.data self.Y[ind, :] = y.float() dist = (u.unsqueeze(1) - self.U.unsqueeze(0)).pow(2).sum(dim=2) y = (y @ self.Y.t() == 0).float() loss = (1 - y) / 2 * dist + y / 2 * (self.m - dist).clamp(min=0) loss1 = loss.mean() loss2 = config["alpha"] * (1 - u.sign()).abs().mean() return loss1 + loss2
完整的代码可以参考博客开头的链接。
实验结果
代码运行结果如下，在五个数据集上进行了测试，由于骨干网络用的AlexNet，因此结果肯定比直接用作者原始定义的那个浅层网络效果要好很多。
| dataset | this impl. | paper |
| cifar10 | 0.774 | 0.6755 |
| nus_wide_21 | 0.766 | 0.5621 |
| ms coco | 0.655 | - |
| imagenet | 0.576 | - |
| mirflickr | 0.735 | - |
