首师大附中集训D2日报（20231211）-题解部分

闲言少叙

T1

给定n个区间，你需要求出能够最多选出多少对区间.
使得两个区间不交。要求一个区间最多属于一对选出的区间。
n<=5e5

5e5打网络流，我好像脑子有问题

---

贪心

区间问题，只要想到贪心，大概率要排序

这道题其实对于左右排序是对称的

可能从左边开始排比较符合人类思维一点（？

1.贪

用最简单的操作维护全局的问题，这是贪心的精髓

从左到右扫一遍，能匹配的就匹配，再显然不过了

2.心

保证正确性是贪心的关键，伪证可能会导致误用贪心，或者贪心题不用贪心，下场悲惨

如果一条边匹配不了，应该把它扔在旁边，用他的右界继续等着后边的左界来匹配

那么问题来了，这样一定会丢解，Hack一下

--1==2---------------- 1
---------3==4--------- 2
---------3======5----- 3
----------------5==6-- 4

如果直接按照左界排好的跑，只有区间1和2匹配

但是按照1-3,2=4可以匹配两组，这是因为3明明可以和1匹配，却叫2抢了先，2虽然左界也符合要求，但是可以用更优的右界去匹配后边的区间

所以我们要想办法让3可以替换2，把2解放出来和后面配对

分析到这里，反悔贪心已经呼之欲出了

实现上，直接开两个优先队列，一个维护等待匹配的区间，一个维护已经配对好的右区间

对于一条边，先尝试匹配，然后尝试替换右区间，最后啥都不行扔到待操作队列里

---

T2

给定一张大小为的有向图。
现在告诉你敌军大本营在节点s和友军基地在节点t。
你需要在每个点上放置一定数量的APERS bounding mine
来杀伤敌方步兵。

为了达成战术效果，
你需要保证任何一条从到的路径都会经过至少个地雷。
由于地理限制，每个节点上只能放置最多一个地雷，
且在u号节点上安放一个地雷需要付出的代价c[u]。

你需要计算出达成战术效果所需付出的最小代价。
n<=200 m<=500 k<=5

不是费用流，是最小割

最小割建模好题

---

可以先简化一下问题，假如点权变成边权

1.从k=1时考虑，相当于裸的最小割

2.考虑k的时候，只需要连INF边限制必须一步一步割就可以了

大概图是这样的

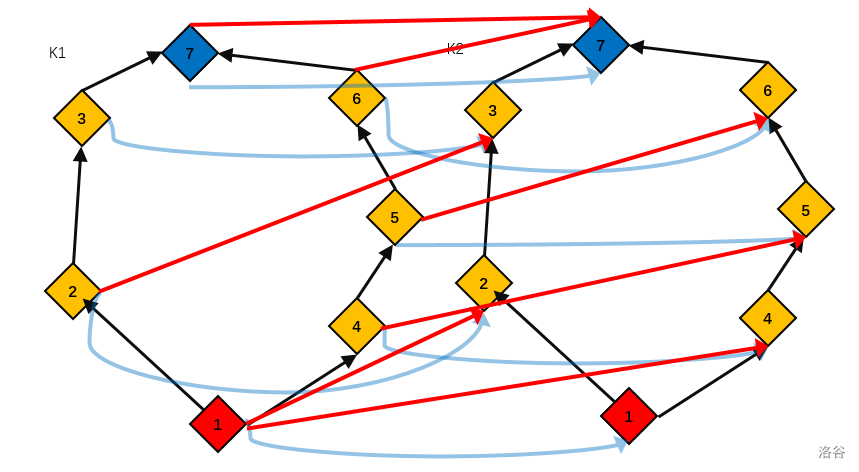
有点抽象 但是可以看懂 就是建分层图，用INF边连图的框架，用带权边还原原图的路径，然后直接割

---

这个思路也可以用在这道题当中，当然这道题给的是点权，要复杂很多，建复杂模型一定要一点点推理

1.k为5，不算大可以直接分k层（以下图用k=3为例），每层图之间先用INF边连相同的点

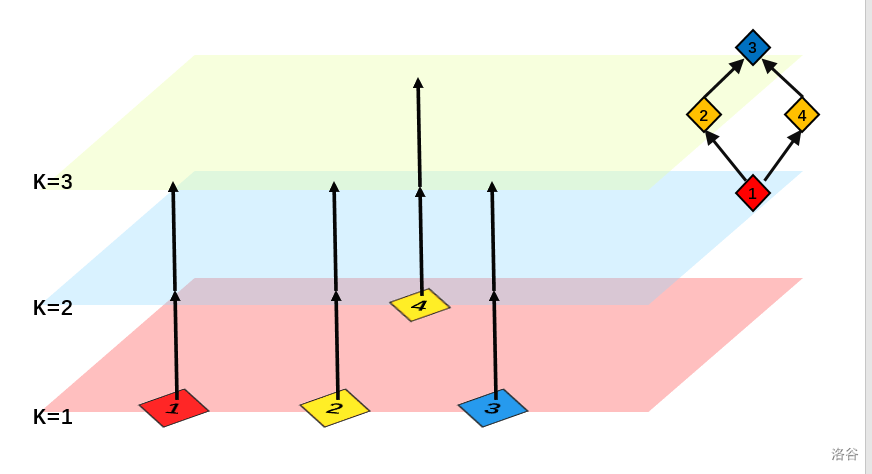
2.最关键的一步，既然给的是点权，最小割又针对的是边权，就建虚点，把点权转化为边权，框架上的点成为点0，从点连一条边，终点就称为点1

事实上，这一步决定了能否用最小割想出这道题

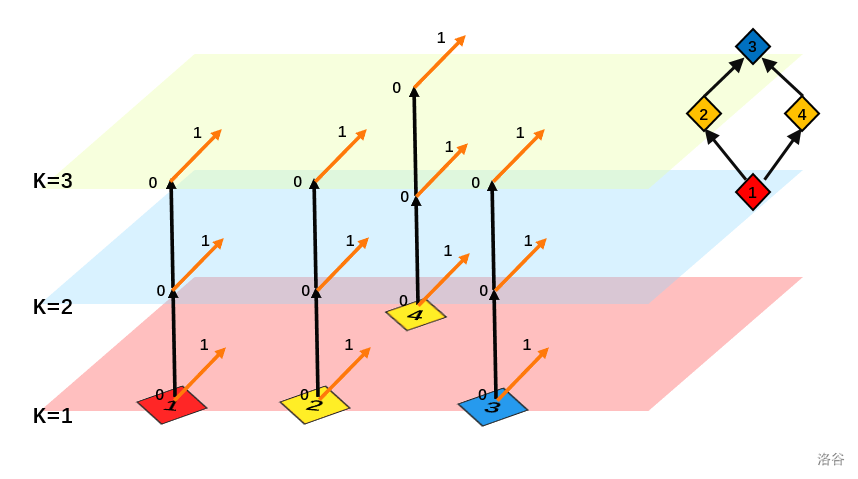
黄色的边边权连成 \(c[i]\)

3.连边，从下向上一层层连就行了

因为我们想达到的效果是通过一个点（黄色边）可以割掉一层，所以用INF边把u1点和v0点连起来，相当于把u1点绑在终点上，割掉黄边就把终点的流断下去了

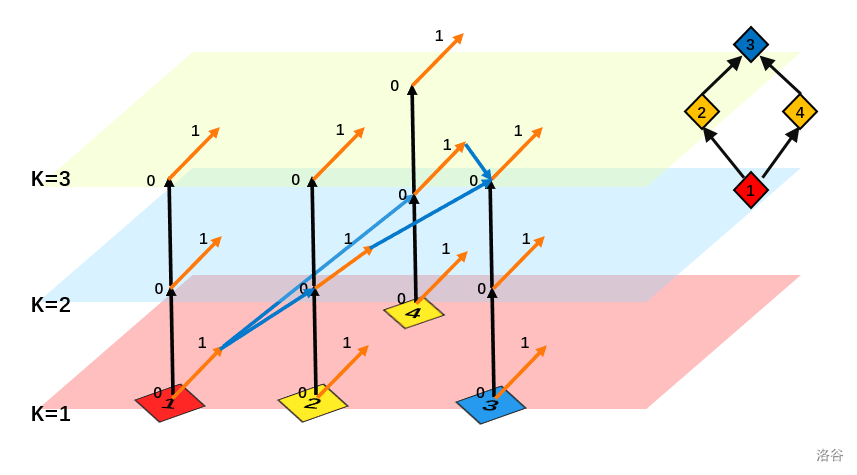
为了简洁，只画了这张图上断掉的边

4.限制条件，每个点只能向上走一层，也就是割边不能跳层，为了让跨层断边不起作用，每个点从下到上，从0->1连INF边

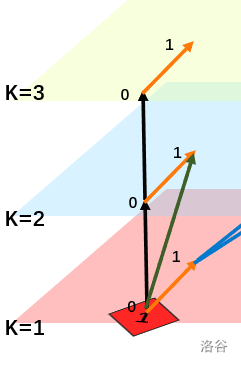
连法如图，为了简洁不全都画出来

最后原点就连在出发点的最下面（0），汇点连在到达点的k层（1）,连出效果如图（部分边省略）

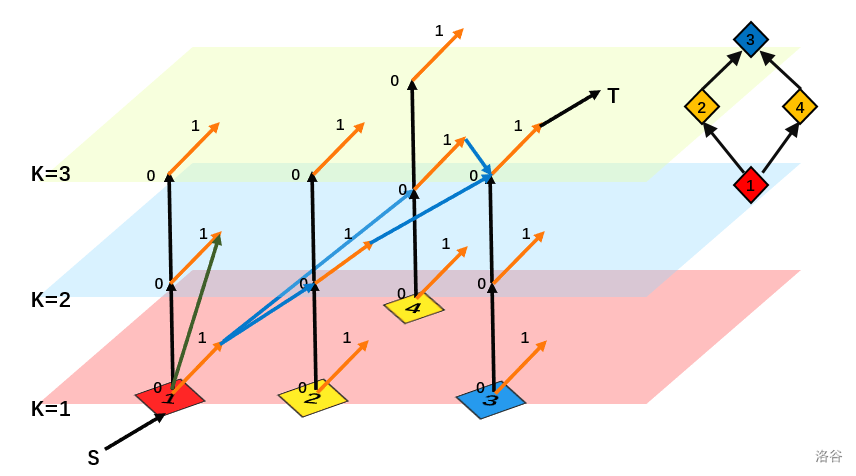
没了，建模一定要耐心，把所有问题分析到

贴上连边代码

cin>>n>>m>>k>>p1>>p2;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=k;j++){
			id[i][j][0]=++cnt;
			id[i][j][1]=++cnt;
		}
	s=++cnt;t=++cnt;
	for(int i=1;i<=n;i++) cin>>c[i];
	
	for(int i=1;i<=n;i++)
	for(int j=1;j<=k;j++)
	 add(id[i][j][0],id[i][j][1],c[i]);
	
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		for(int j=1;j<=k;j++){
			add(id[u][j][1],id[v][j][0],INF);
		}
	}
	
	for(int i=1;i<=n;i++)
	for(int j=1;j<k;j++){
	 add(id[i][j][0],id[i][j+1][0],INF);
	 add(id[i][j][0],id[i][j+1][1],INF);
	}
	 
	add(s,id[p1][1][0],INF);
	add(id[p2][k][1],t,INF);
	int tmp=dinic();
	if(tmp==INF) cout<<-1;
	else cout<<tmp;

T3 先不写了，回头更新，写网络流去了