汉诺塔实现方法

首选，规定一个包含有栈的类，对应抽象汉诺塔

        class HanoiStack
        {
            public string TowerName { get; set; }     //对应汉诺塔的塔名称，如：A,B,C
            public Stack<int> TowerStack { get;set; } //栈，先进后出，跟汉诺塔的玩法很相符
        }

然后，汉诺塔的搬运规则，其核心就是：当若只有一个盘时，直接将盘从源塔柱搬移到目标塔柱，否则，递归上一步搬移，直至仅有一个盘

即，n=1，源塔柱 --> 目标塔柱；n>1，递归直至仅有一个盘

        /// <summary>
        /// 汉诺塔搬运规律
        /// </summary>
        /// <param name="n">总的盘数</param>
        /// <param name="from">源塔柱</param>
        /// <param name="to">目标塔柱</param>
        /// <param name="transfer">中转塔柱</param>
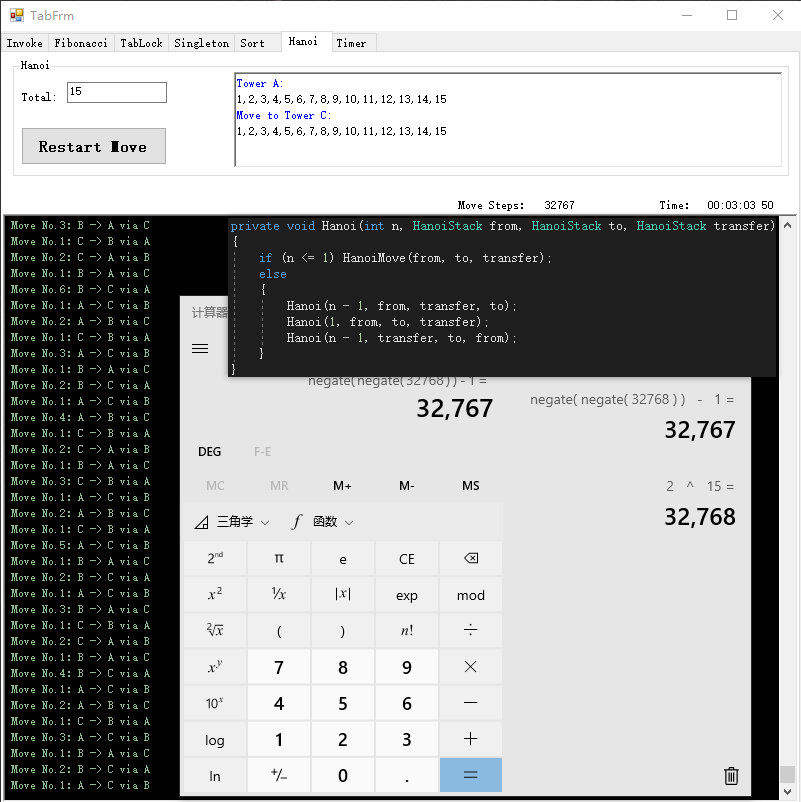
        private void Hanoi(int n, HanoiStack from, HanoiStack to, HanoiStack transfer)
        {
            if (n <= 1) HanoiMove(from, to, transfer);  //只有一个盘，则直接从源塔柱搬移到目标塔柱，否则递归直至仅有一个盘
            else
            {
                Hanoi(n - 1, from, transfer, to);
                Hanoi(1, from, to, transfer);
                Hanoi(n - 1, transfer, to, from);
            }
        }

再就是，搬运以及打印显示，打印显示的方式个人开心就好

        private void HanoiMove(HanoiStack from, HanoiStack to, HanoiStack transfer)
        {
            to.TowerStack.Push(from.TowerStack.Pop());  //搬运，从 源塔柱 中取出最顶端的一个“盘”，放入 目标塔柱 的顶端
            RichTextBoxAppendLine(richTextBox_Hanoi, $" Move No.{to.TowerStack.Peek()}：{from.TowerName} -> {to.TowerName} via {transfer.TowerName}", Color.DarkSeaGreen, true);  //打印显示
        }

最后，函数调用

        private void Hanoi_Start(int total)
        {
            int n = total;
            HanoiStack a = new HanoiStack() { TowerName = "A", TowerStack = new Stack<int>() };
            HanoiStack b = new HanoiStack() { TowerName = "B", TowerStack = new Stack<int>() };
            HanoiStack c = new HanoiStack() { TowerName = "C", TowerStack = new Stack<int>() };
            while (total-- > 0) a.TowerStack.Push(total + 1); //初始化栈
            Hanoi(n, a, c, b);
        }　　

运行效果，测试用例是：15，汉诺塔的搬移步骤总数为，2 的 n 次方减 1，即：2^n-1，

当 n=15，搬移的步骤总数为：2^15-1 = 32767，

运行结果，搬移步骤总数为 32767，耗时 03分03秒 50毫秒

搬移过程，下图所示，如：Move No.1：A -> C via B   ，

　　表示：将1号盘（No.1）从 A 塔柱通过 B 塔柱搬移到 C 塔柱

　　实际操作为：直接将 1号盘（No.1）从 A 塔柱搬移到 C 塔柱

　　

 

---

 

 

author：韦小明

本文即原文：汉诺塔实现方法

本文路径：https://www.cnblogs.com/youler/p/13814935.html