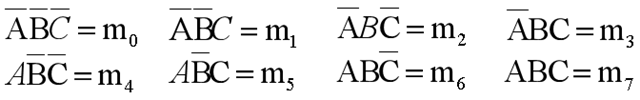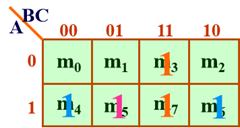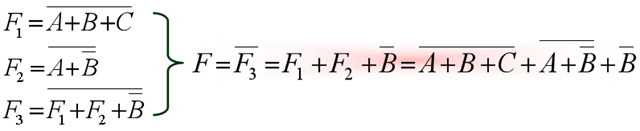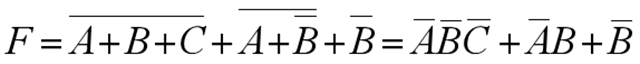第八章 组合逻辑电路
数字电路用于对数字量信息进行传送、运算、变换、比较、存储等操作。按逻辑功能的特点不同,可以把数字电路分成两类: 组合逻辑电路和时序逻辑电路,本章仅介绍组合电路。
组合逻辑电路(Combinational Logic Circuit)的功能特点是:电路在任意时刻的输出状态,仅决定于该时刻输入状态的组合, 而与电路原先的状态无关,也就是说没有记忆功能。 它在电路结构上的特点是由门电路组成的。
最小项与卡诺图
知识点概述:
1、在逻辑函数表达式中,若一个乘积项包含了所有逻辑变量,每个变量以原变量或反变量的形式作为一个因子,并且只能出现一次,则该乘积项(与项)被称为最小项。
2、无论什么形式的逻辑函数都可以展成唯一标准的最小项之和表达式。
3、卡诺图就是按一定规律(逻辑相邻、循环相邻)排列起来的最小项方格图,卡诺图是逻辑函数的一种图形表示。
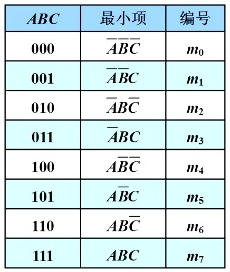
最小项:设有 n 个变量,它们组成的与项中每个变量或以原变量或以反变量形式出现一次,且仅出现一次,这些与项均称之为n个变量的最小项。
若函数包含 n 个变量,就可构成 2n个最小项,分别记为 mn。
两个变量A和B,可以构成四个(22)最小项:
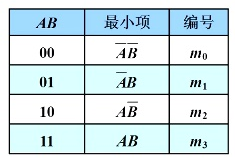
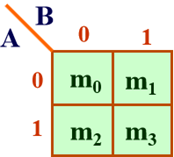
相邻两个变量之间只允许有一个变量不同!
用卡诺图表示逻辑函数
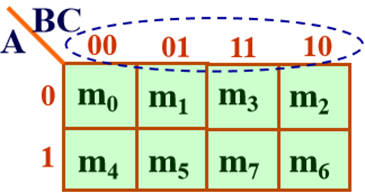
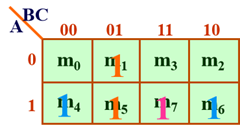
卡诺图是平面方格阵列图,其画法满足几何相邻原则:相邻方格中的最小项仅有一个变量不同。
用卡诺图表示逻辑函数时,将函数中出现的最小项,在对应方格中填1,没有的最小项填0(或不填),所得图形即为该函数的卡诺图。
卡诺图化简
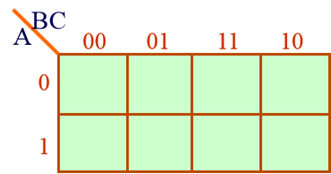
1.根据变量数目画出卡诺图
2.对相邻最小项进行分组合并。圈2个或4个“1”,保留相同项。
3.写出最简与或表达式。
例:用卡诺图化简数 ![]() ,写出其最简与或表达式。
,写出其最简与或表达式。
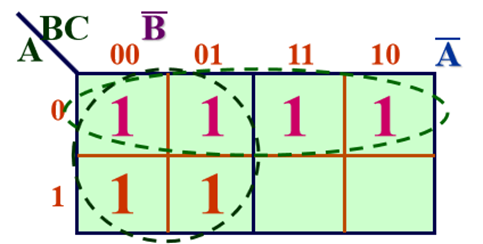
解:有三个变量,所以卡诺图如下,然后填上最小项。接着圈“1”,最后写出 与或 表达式。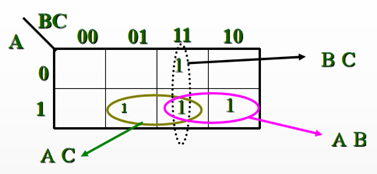
所以化简结果为:![]()
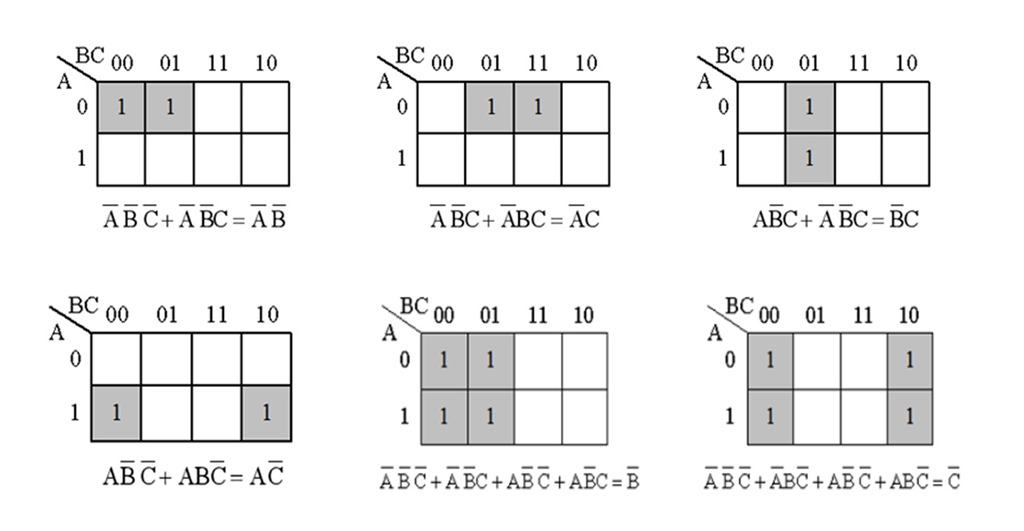
三变量合并最小项的常见情况
一、 组合逻辑电路分析
工程上经常会遇到“读图”问题,组合逻辑电路的分析就是组合逻辑电路的“读图”,即从给定的逻辑电路图中找出电路输入变量和输出变量之间的逻辑关系,进行逻辑功能分析。组合电路分析的一般步骤如下:
(1)根据逻辑图从输入到输出逐级写逻辑表达式,直至写出输出端的逻辑函数表达式。
(2) 用公式法或卡诺图法化简输出端逻辑函数表达式,需要时化为最简式。
(3) 根据化简后的逻辑表达式列真值表,即将各种可能的输入状态组合代入简化了的表达式中进行计算,求出真值表。
(4) 功能评述。根据真值表或函数表达式,概括出对电路逻辑功能的文字描述,并对原电路的设计进行评论,或者提出改进意见。 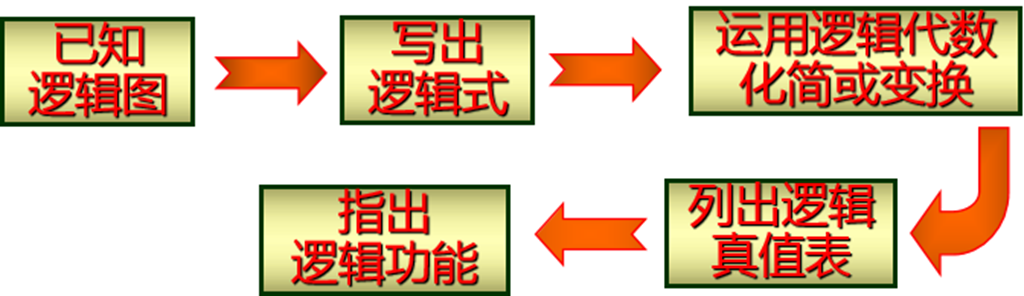
例1:分析下图所示组合电路的功能。
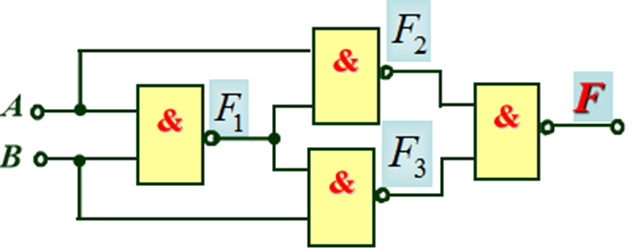
根据逻辑图写出相应逻辑式:
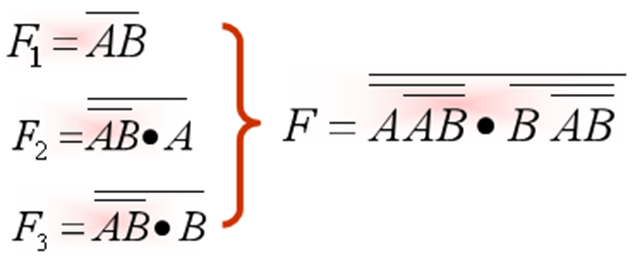
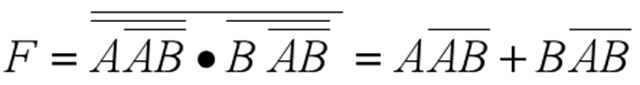 (反演律)
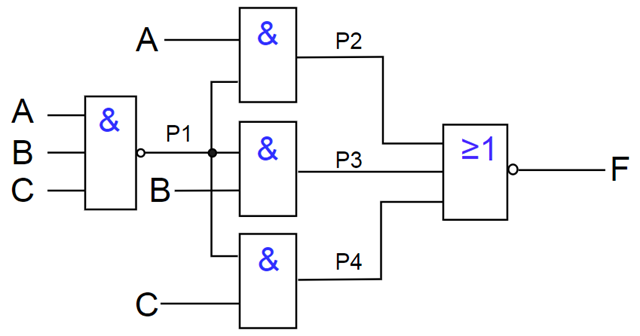
(反演律)例2:分析下图所示组合电路的功能。
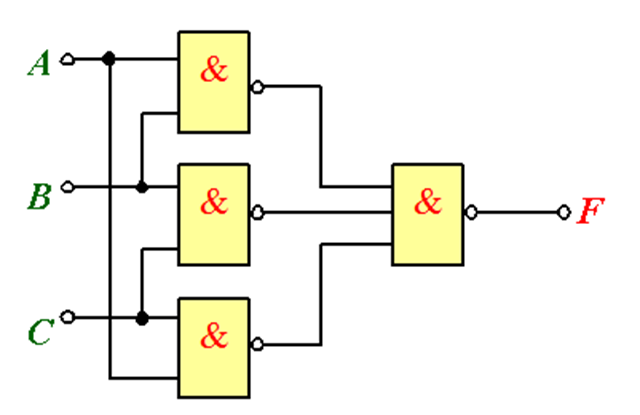
解:根据逻辑图写出相应逻辑式:
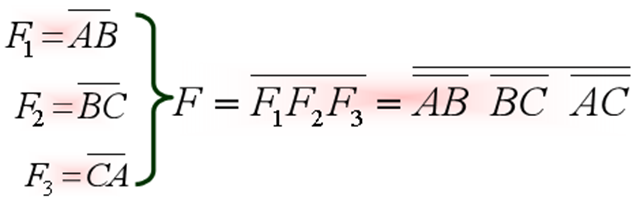
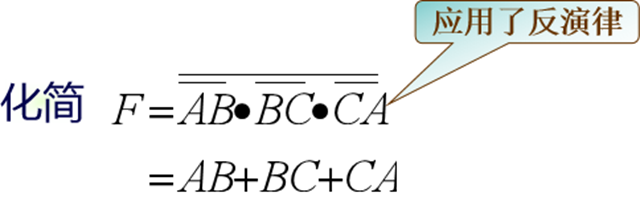
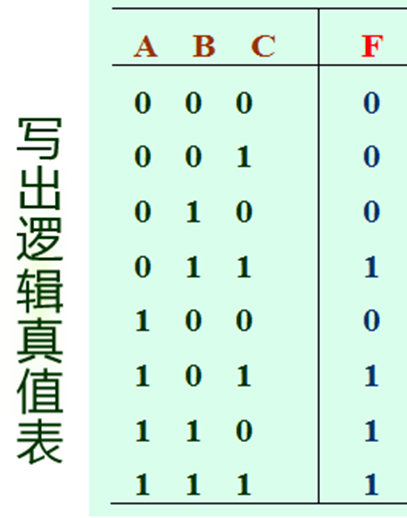
由真值表数据分析
当输入A、B、C中有2个或2个以上为1时,输出F就为1,否则输出F为0。
若输入是裁判,输出是裁定结果,显然该电路是一个多数表决器。
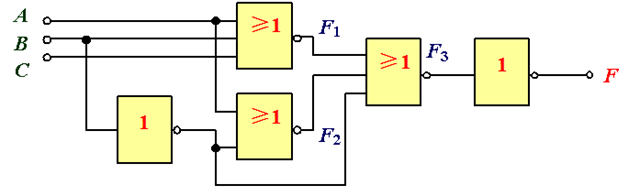
例3:分析图所示电路的逻辑功能。
解 :(1) 逐级写逻辑表达式:
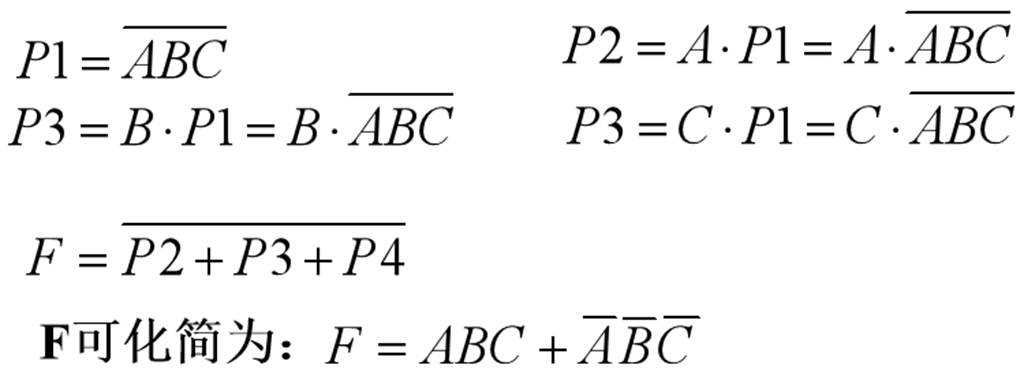
(2)列出真值表:
| A | B | C | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
(3) 逻辑功能分析。由此可知电路的逻辑功能为:当ABC三者输入一致时,F为1;当ABC不相同时,则输出为0。因此该电路判别“不一致电路”。
例4:分析下图所示组合电路的功能。
二、 组合逻辑电路的设计(略)