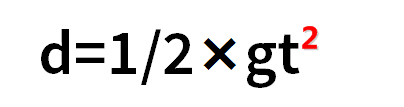Scratch3.0 自由落体实验

同学们知道著名的比萨斜塔实验吗？它证明了一个非常重要的定律，叫做自由落体定律：两个物体，无论它们的重量是否相同，在不计空气阻力的情况下，在同一高度落下，会同时落地。这是一个非常重要的实验，有了它，才会有我们现在这么发达的现在社会生活。

关于这个实验的真实性众说纷纭，其中流传最广的故事是这样的！古希腊权威思想家亚里士多德曾经断言：物体从高空落下的快慢同物体的重量成正比，重者下落快，轻者下落慢。比如说，十磅重的物体落下时要比一磅重的物体落下快十倍。多少年来，人们都把这个错误论断当作真理而信守不移。

直到16世纪，伽利略发现了这一理论在逻辑上的矛盾。伽利略说，假如有质量不同的大小两块石头，按照亚里士多德的论断，质量小些的小石头下落慢，大石头下落快，要是我们把这两块石头捆在一起，那这块重量等于两块石头重量之和的新石头 ，将以何种速度下降呢？

正是伽利略认为亚里士多德的论断存在悖论，于是勇于相信自己，决定向当时的人们证明自己的理论，这就有了著名的比萨斜塔自由落体实验。

了解过上面的故事后，今天我们就来使用Scratch来模拟制作一个自由落体的实验吧。

本程序将模拟自由落体运动。当静止的物体从一定高度下落时，若忽略空气阻力的影响，则在t(秒)时间内，物体下降的距离d(米)由公式：

确定，其中g是重力加速度，取值g=9.8m/s2。

本模拟实验的目的是标记出下落的物体小球在0.5秒、1秒、1.5秒、2.0秒等时间的位置，直到小球到达地面。该模拟实验的界面如图7-29所示。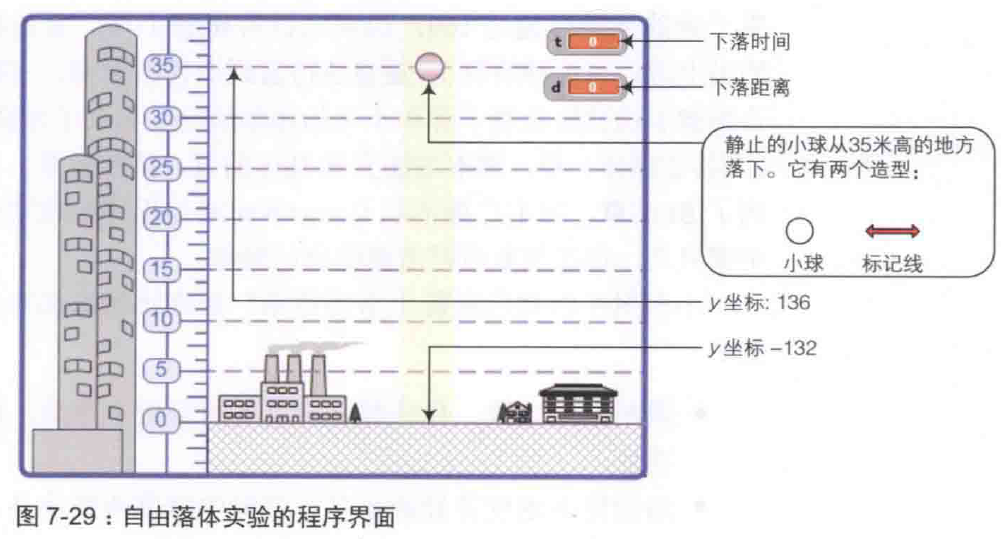

程序中的小球处于静止状态，现在模拟它从35米的高度落下的情形。该程序仅有一个角色ball，其中包含两个造型。当到达了标记的时间时，角色快速切换到造型marker，印一个图章，再重新切换到造型ball。

图上可知，小球从y=136处下落，地面是y=-132，一共是268步长，对应35米的高度，则每米对应268/35 步，即268/35（步/米）。小球下落距离d时对应268/35*d 步，则小球的y=136-268/35*d

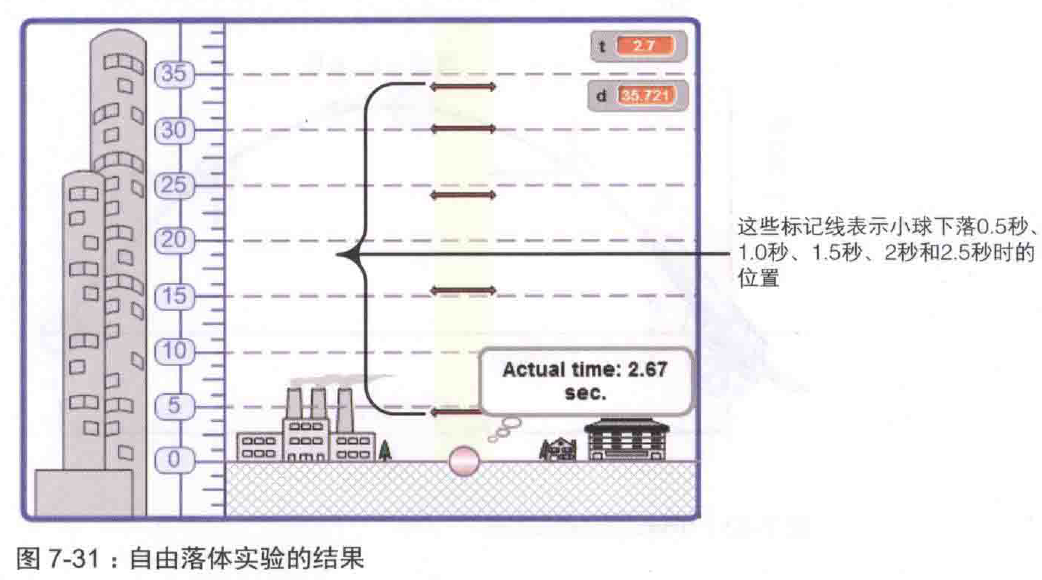
我们用counter变量来计录循环次数，每次循环0.05秒，所以当循环10、20、30、40…次时，即是0.5、1、1.5、2…秒。下图展示了本模拟实验的最终效果。可以看出小球越落越快，这是因为受了重力加速度的作用。

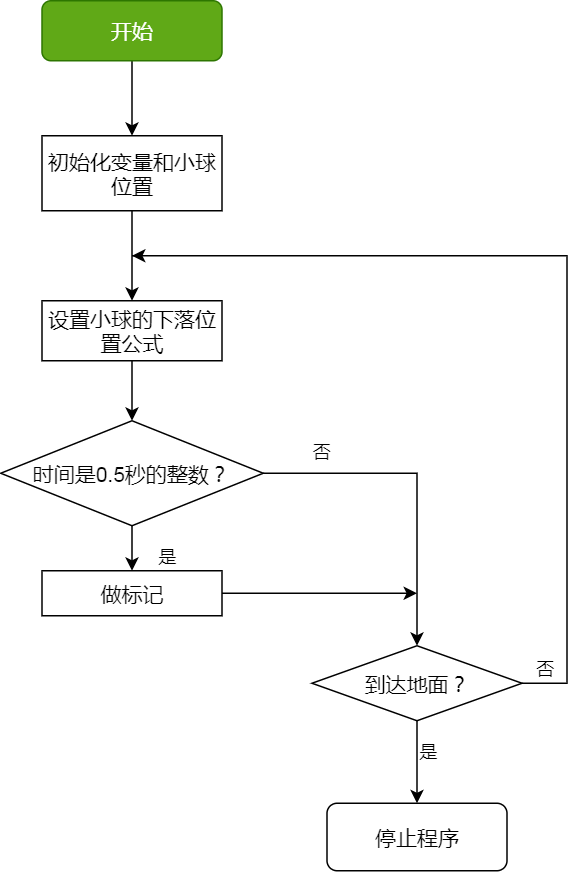
流程图如下