向量运算(lua,三维) 点乘、叉乘、模、夹角
向量运算在游戏制作中经常用到,稍微总结一下。
一、点乘
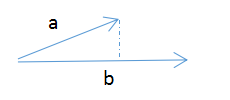
如图,假设![]()
![]()
向量a与b的点乘表示a在b上的投影与b的模的乘积
公式:
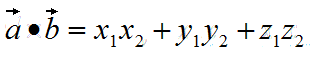
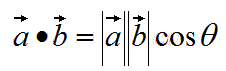
代码:
function MathHelper.GetVector3Dot(v1, v2)
return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z
end
二、叉乘
向量的叉乘,即求同时垂直两个向量的向量
公式:

代码:
-- 向量叉乘
function MathHelper.GetVector3Cross(v1, v2)
local v3 ={x = v1.y*v2.z - v2.y*v1.z , y = v2.x*v1.z-v1.x*v2.z , z = v1.x*v2.y-v2.x*v1.y}
return v3
end
三、模
向量的长度
公式:
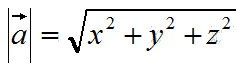
代码:
-- 向量的模
function MathHelper.GetVector3Module(v)
return math.sqrt(v.x * v.x + v.y * v.y + v.z * v.z)
end
四、夹角
公式:
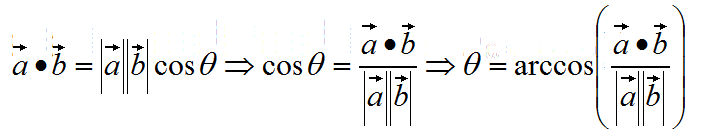
代码:
-- 求两向量间夹角
function MathHelper.GetVector3Angle(v1, v2)
local cos = MathHelper.GetVector3Dot(v1, v2)/ (MathHelper.GetVector3Module(v1)*MathHelper.GetVector3Module(v2))
return math.acos(cos) * 180 / math.pi
end
完整代码:

1 MathHelper = {}
2 -- 向量点乘
3 function MathHelper.GetVector3Dot(v1, v2)
4 return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z
5 end
6
7 -- 向量叉乘
8 function MathHelper.GetVector3Cross(v1, v2)
9 local v3 ={x = v1.y*v2.z - v2.y*v1.z , y = v2.x*v1.z-v1.x*v2.z , z = v1.x*v2.y-v2.x*v1.y}
10 return v3
11 end
12
13 -- 向量的模
14 function MathHelper.GetVector3Module(v)
15 return math.sqrt(v.x * v.x + v.y * v.y + v.z * v.z)
16 end
17
18 -- 求两向量间夹角
19 function MathHelper.GetVector3Angle(v1, v2)
20 local cos = MathHelper.GetVector3Dot(v1, v2)/ (MathHelper.GetVector3Module(v1)*MathHelper.GetVector3Module(v2))
21 return math.acos(cos) * 180 / math.pi
22 end




