请问二叉树等数据结构的物理存储结构是怎样的？

　　请问二叉树等数据结构的物理存储结构是怎样的？

　　好吧，咱们书上说了，一般两种存储方式: 1. 以完全二叉树的形式用连续空间的数组存储; 2. 以链表形式存储,即各个数据之间保存了相关的数据的指针地址！
　　如果回答就是这样，那么我想大家也不费那神了，直接洗洗睡吧？咱们能不能深入点？ 

　　数组是好理解的，在内存在磁盘都是一样的，连续相邻的空间，挨着存放到磁盘就可以了；好吧，就算你正确？那么链表呢？拿简单的单链表来说，上一个节点保存下一个节点的指针？是如何保存的？我们能想到的，就是一个上一节点存储了下一节点的绝对地址或者偏移地址，好像是这样的！

　　那么问题来了，这个下一节点地址到底是什么样的呢？是相对地址还是绝对地址？这个地址是怎么算出来的？存储在内存上是肯定没有问题的！但是如果存储在磁盘上呢？如果这个地址是固定的，那么，如果换了硬盘（换了存储介质），是否就找不到该地址（因为每个设备的地址自然是不一样的）？

　　针对这个问题，很是困扰了我很久！也询问过几个身边的小伙伴，也都说不知道。后来在一次面试中，一面试官刚好问我这问题，我把自己的见解说完后，说我确实不知道是怎么存储的。最后我要求他给予答案，然后，他说，就是存储的下一节点的地址（内存地址），压根不存在什么数据结构存储于磁盘这种说法，内存中，是动态计算的值。如果存在内存拷贝，那么，也会重新计算这些地址的，所以看起来相同的结构，在不同存储工具上，会会表现出不同的地址空间。

　　好吧，我将信将疑！被丢了n个鄙视的表情，然后被pass掉了。

　　那么，到底内存中的二叉树怎么存储在硬盘上的呢？

　　其实硬盘上并没有什么二叉树的，硬盘只是充当了一个存储介质，只是提供你要读的时候可以取而已，而真正的数据结构，则需要在用的时候再还原出原来的树形结构！

下面以一个简单的示例来展示磁盘上的数据结构的存储方式:

 

public class BinTreeDiskSample {
    private static int h = -1;
    private static Node root;
    static class Node implements Serializable {
        private static final long serialVersionUID = -4780741633734920991L;
        int data;
        transient Node left;
        transient Node right;
        int lHeight = -1, rHeight = -1;
        public Node(int data) {
            this.data = data;
        }
        public Node setLeft(Node left) {
            this.left = left;
            return this;
        }
        public Node setRight(Node right) {
            this.right = right;
            return this;
        }
        public Node getLeft() {
            return left;
        }
        public Node getRight() {
            return right;
        }
        // 后续遍历写入，先序遍历读出
        public int write(ObjectOutputStream out) throws IOException {
            if (left != null) {
                lHeight = left.write(out);
            }
            if (right != null) {
                rHeight = right.write(out);
            }
            h++;
            out.writeObject(this);
            return h;
        }
        private void init(List<Node> list) {
            if (lHeight != -1) {
                left = list.get(lHeight);
                left.init(list);
            }
            if (rHeight != -1) {
                right = list.get(rHeight);
                right.init(list);
            }
        }

    }
    public static void binTreePreOrderPrint(Node root) {
        System.out.print(root.data + " ");      // visit root
        if(root.left != null) {
            binTreePreOrderPrint(root.left);
        }
        if(root.right != null) {
            binTreePreOrderPrint(root.right);
        }
    }
    // 先序遍历读出
    public static void read(ObjectInputStream in) throws IOException,
            ClassNotFoundException {
        List<Node> list = new ArrayList<Node>();
        Node n;
        Object obj;
        try {
            while ((obj = in.readObject()) != null) {
                n = (Node) obj;
                list.add(n);
            }
        }
        catch (Exception e) {
            // EOFException ...
//            e.printStackTrace();
        }
        root = list.get(list.size() - 1);
        root.init(list);
    }
    public static void main(String args[]) throws FileNotFoundException,
            IOException, ClassNotFoundException {
        // 构造一棵二叉树 11 21 41 61 51 31
        Node n6 = new Node(61);
        Node n4 = new Node(41).setLeft(n6);
        Node n5 = new Node(51);
        Node n2 = new Node(21).setLeft(n4).setRight(n5);
        Node n3 = new Node(31);
        Node n1 = new Node(11).setLeft(n2).setRight(n3);
        root = n1;
        System.out.println("output node: ");
        binTreePreOrderPrint(root);
        // 将数据写稿磁盘
        ObjectOutputStream out = new ObjectOutputStream(new FileOutputStream("btree.bin"));
        root.write(out);
        out.close();

        root = null;
        // 将数据从磁盘读入，并进行数据结构的重新构建
        ObjectInputStream in = new ObjectInputStream(new FileInputStream("btree.bin"));
        read(in);
        in.close();
        System.out.println("\nread node: ");
        binTreePreOrderPrint(root);
    }

}

 

输出：

 

如上二叉树的磁盘存储，使用了java自带的序列化工具，将节点写入磁盘（注：这并不是一种好的实践），然后在读出的时候，按照写稿时候的规则，进行重新构建二叉树即可。

 所以：

　　存储磁盘的数据结构，只是一种约定的方式，只是为了方便在重新恢复链表，二叉树等等内存结构的算法而已。

　　如：数据库索引是存储在磁盘上，当表中的数据量比较大时，索引的大小也跟着增长，达到几个G甚至更多。当我们利用索引进行查询的时候，不可能把索引全部加载到内存中，只能逐一加载每个磁盘页，这里的磁盘页就对应索引树的节点。

B+/-树索引用使用很多的数据结构，下面做一点简单介绍：

一、B-Tree
　　m阶B-Tree满足以下条件：

　　1、每个节点最多拥有m个子树

　　2、根节点至少有2个子树

　　3、分支节点至少拥有m/2颗子树（除根节点和叶子节点外都是分支节点）

　　4、所有叶子节点都在同一层、每个节点最多可以有m-1个key，并且以升序排列

二、B+Tree的定义
　　B+Tree是B树的变种，有着比B树更高的查询性能，来看下m阶B+Tree特征：

　　1、有m个子树的节点包含有m个元素（B-Tree中是m-1）

　　2、根节点和分支节点中不保存数据，只用于索引，所有数据都保存在叶子节点中。

　　3、所有分支节点和根节点都同时存在于子节点中，在子节点元素中是最大或者最小的元素。

　　4、叶子节点会包含所有的关键字，以及指向数据记录的指针，并且叶子节点本身是根据关键字的大小从小到大顺序链接。

 

下面让我们来看看现代数据库的磁盘存储结构吧：

以下部分内容摘自： https://blog.csdn.net/qq910894904/article/details/39312901 

　　我们都知道，数据库通常使用B+树作为索引，但是国内很少有人提到数据库使用的是HeapFile来管理记录的存储。国外的一些大学在“数据库系统实现”这门课上通常会让学生实现一个简单的数据库，因此有不少HeapFile的资料。

基于Page的HeapFile
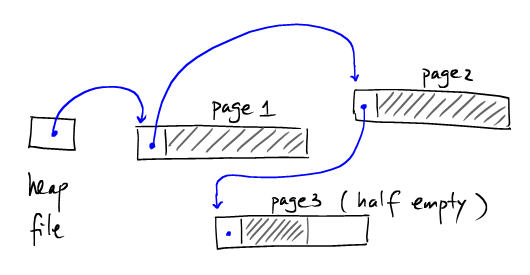
　　采用链表形式的是HeapFile如下：

　　Heap file和链表结构类似的地方：

　　　　支持增加（append）功能
　　　　支持大规模顺序扫描
　　　　不支持随机访问

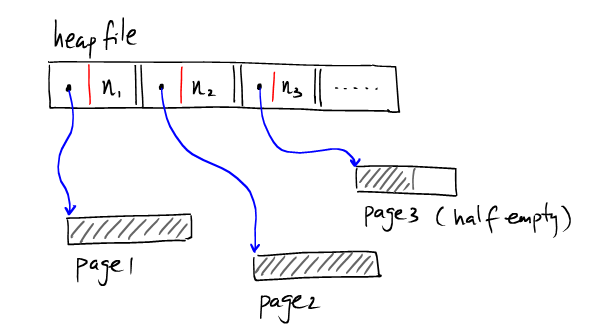
　　这种方式的HeapFile在寻找具有合适空间的半空Page时需要遍历多个页，I/O开销大。因此一般常用的是采用基于索引的HeaFile.在HeapFile中使用一部分空间来存储Page作为索引，并记录对应Page的剩余量。如下：

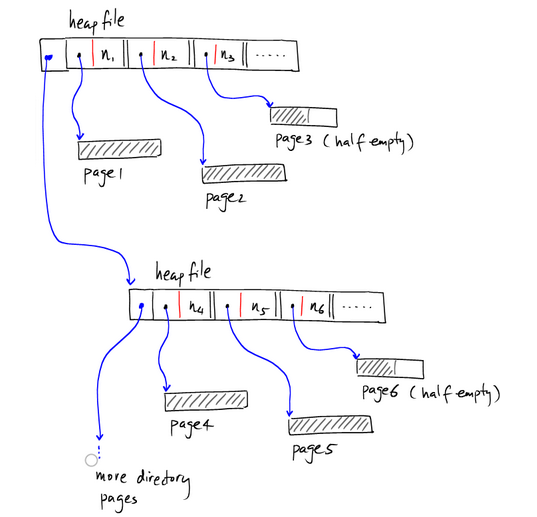
像上图那样，索引单独存在一个page上。数据记录存在其他page上，如果有多个索引的page，则可以表示为：

下面是Heap file自有的一些特性：

数据保存在二级存储体（disk）中：Heapfile主要被设计用来高效存储大数据量，数据量的大小只受存储体容量限制；

Heapfile可以跨越多个磁盘空间或机器：heapfile可以用大地址结构去标识多个磁盘，甚至于多个网络；

数据被组织成页；

页可以部分为空（并不要求每个page必须装满）；

页面可以被分割在某个存储体的不同的物理区域，也可以分布在不同的存储体上，甚至是不同的网络节点中。我们可以简单假设每一个page都有一个唯一的地址标识符PageAddress，并且操作系统可以根据PageAddress为我们定位该Page。

一般情况下，使用page在其所在文件中的偏移量就可以表示了。