<数据结构与算法分析>读书笔记--递归
一、什么是递归
程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回(引用百度百科)。
由此可概括递归有如下几个特点?
(1)一个函数或者某个额过程直接或者间接的调用自己；
(2)大型问题小型化；
(3)类似于循环;
(4)需要边界条件，当边界条件满足时，返回对应的值，当不满足时，继续前进。
1.一个简单的递归方法
代码示例:
package cn.recursive.example;
public class RecursiveExample {
/**
* 一个递归方法
* @param x
* @return
*/
public static int f(int x) {
if (x == 0) {
return 0;
}
return 2 * f(x - 1) + x * x;
}
public static void main(String[] args) {
//调用该方法，当x=2时，输出为6
System.out.println(RecursiveExample.f(2));
}
}
描述:
以x值为基准，当x=0时，返回0，否则 执行 2 * f(x-1) + x * x
其中 f(x-1)实际就是上述的静态方法，只不过在此做了计算处理。
2.递归容易混淆的概念
比较常见的问题就是:它是否就是循环推理。
我的回答是:比如1中的代码，从某种角度上看，每一次给x赋值后，到最后通过类.方法进行调用输出，在此过程中推理的表现比如对值比较判断，比如当x==0的时候返回0，不为0的时候执行else，而else中2 * f(x-1) + x * x的 f(x-1)循环调用了f(x)，只不过该f(x)做了计算处理减1。
书中作者给的回答是:
虽然我们定义一个方法用的是这个方法的本身，但是我们并没有用方法本身定义该方法的一个特定的实例。换句话说，通过f(5)来得到f(5)的值才是循环的。通过f(4)来得到f(5)不是循环的，当然了，除非f(4)的值又要用到对f(5)的计算。
再来一段无终止递归方法代码示例:
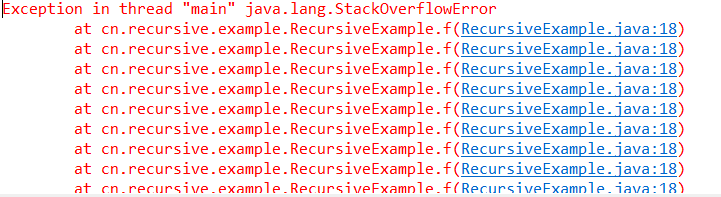
package cn.recursive.example; public class RecursiveExample { /** * 无终止递归方法 * @param n * @return */ public static int bad(int n) { if (n==0) { return 0; }else { return bad(n/3+1) +n-1; } } public static void main(String[] args) { //无终止递归方法,会报错，报错信息主要是栈异常 System.out.println(RecursiveExample.bad(1)); } }
运行后，报的错与前面f(-n)是一致的。而只有当n=0时才不会报错。
作者这样分析，以bad(1)为例，bad(1)究竟是多少，这个定义给不出任何答案，因此，计算机将会反复调用bad(1)以期望解出它的值。最后，计算机簿记系统占满内存，程序崩溃。
不管b(n)中的n处于何值，它们的值都不能求出，比如bad(100)，bad(100)会一直调用b(99)、b(98)、b(97)等等，最后它们的值还是求不出来。
事实上，除了0以外，这个程序对n的任何非负值都无效。对于递归程序，不存在像“特殊情形“这样的情况。
由此我们根据上面的讨论可以推出递归的前两个基本法则:
(1)基准情形。必须总要有某些基准情形，它们不用递归就能求出正解。
(2)不断推进。对于那些要递归求解的情形，递归调用必须总能够朝着一个基准情形推进。
递归的第三个法则是设计法则
(3)设计法则。假设所有的递归调用都能运行。
这是一条重要的法则，因为它意味着，当设计递归程序时一般没有必要知道簿记管理的细节，你不必试图追踪大量的递归调用。追踪具体的递归调用的序列常常是非常困难的。当然，在许多情况下，这正是使用递归好处的体现，因为计算机能够算出复杂的细节。
递归的主要问题是隐含的簿记开销。虽然这些开销几乎总是合理的(因为递归程序不仅简化了算法设计而且也有助于给出更加简洁的代码)，但是递归绝不应该作为简单for循环的替代品。
当编写递归例程时，关键要牢记递归的四条基本法则(将上面的合成到这里来，顺便补充一条):
(1)基准情形。必须总要有某些基准情形，它无需递归就能解出。
(2)不断推进。对于那些需要递归求解的情形，每一次递归调用都必须要使状况朝向一种基准情形推进。
(3)设计法则。假设所有的递归调用都能运行。
(4)合成效益法则。在求解一个问题的同一实例时，切勿在不同的递归调用中做重复性工作。
上述代码示例可在我的Github上找的到，代码地址为:https://github.com/youcong1996/The-Data-structures-and-algorithms/tree/master/Introduction
二、递归的应用场景
(1)以我Linux曾经犯的一个低级错误来说，常常使用rm -rf 删除文件以至于最后不小心删除了boot，其中rm -rf就是递归删除文件。
(2)在代码专利申请的时候，通常我们需要将代码输出到一个txt文件然后将其转成pdf或者word，这时如果代码量几十万行或者三四万行，一个个手动复制将是一件多么可怕的事情，这个时候就可以用递归找到*.java文件并将其输出到对应的txt上。
