第三次的课程 条件概率，全概率，贝叶斯公式

1.条件概率： 已知某个事件A发生的条件下，另一个事件B发生的概率称为条件概率，记为P(B|A)

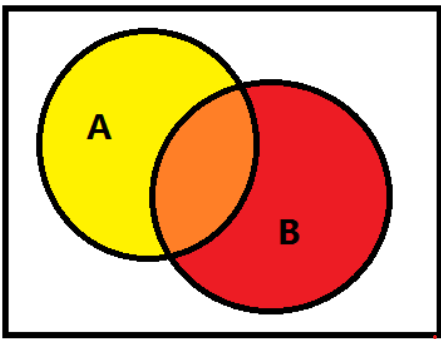
看一下P(B|A)与P(A)、P(B)的关系：P(B|A)=P(AB)/P(A)

条件概率的三个条件：

1. 非负性：P(B|A) ≥0;
2. 规范性：对于必然事件S，有P(S|A)=1
3. 可列可加性：对于两两互不相容的事件𝐵1， 𝐵2， 𝐵3……，即𝐵𝑖 · 𝐵𝑗= ∅，i ≠j， i,j=1,2,……，有𝑃(𝐵1 ∪ 𝐵2 ∪……|A)=P(𝐵1|A)+P(𝐵2|A)+……

乘法定理： 

P(AB)=P(B|A)P(A)，其中P(A)>0

易推广到P(ABC)=P(C|AB)P(B|A)P(A)=P(A|BC)P(B|C)P(C)

全概率公式

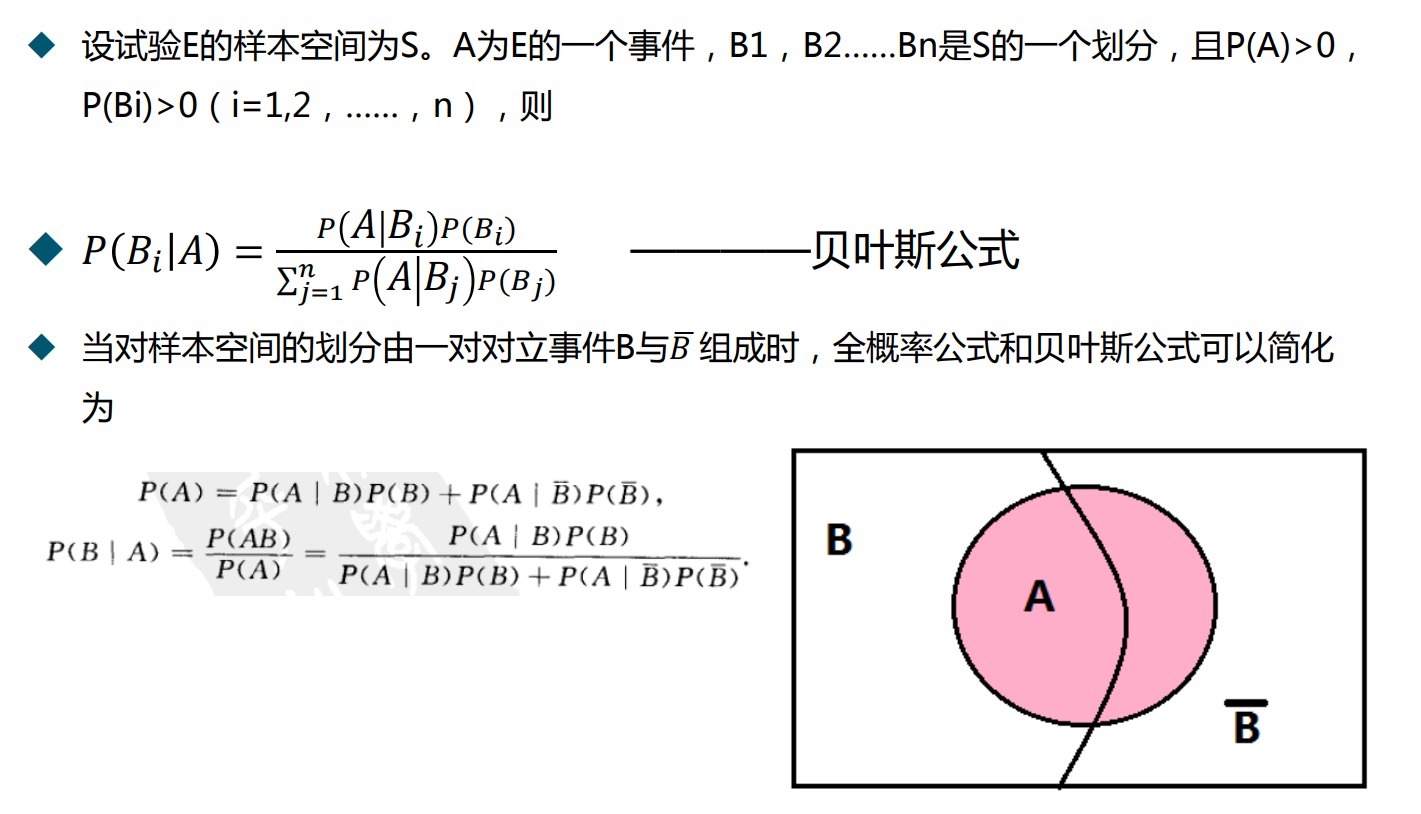
设试验E的样本空间为S，Ａ为Ｅ的一个事件，B1,B2……Bn是S的一个划分，且 P(Bi)>0(i=1,2……n)，则

P(𝐴) = 𝑃 (𝐴| 𝐵1) 𝑃(𝐵1) + 𝑃 (𝐴 |𝐵2) 𝑃(𝐵2) + ⋯ + 𝑃 (𝐴| 𝐵𝑛) 𝑃(𝐵𝑛)

 

2.贝叶斯公式

推导过程：

 

 概念定义：

 

 

 

3.公式比较 乘法公式、全概率公式与贝叶斯公式

1. 乘法公式是求“几个事件同时发生”的概率；
2. 全概率公式是求“最后结果”的概率； 
3.  贝叶斯公式是已知“最后结果” ，求“某个事件”的概率.

先验概率与后验概率

1. P(Bj|A)是在事件A发生的条件下, 某个事件Bj发生的概率, 称为 “后验概率”; 
2. Bayes公式又称为“后验概率公式”或“逆概公式”; 
3. 称P(Bj) 为“先验概率”.

4.独立性

设A、B是两个事件，如果满足：P(AB)=P(A)P(B)，则称事件A、B相互独立。简称A、 B独立。

由事件独立的定义可以推出： 

1. A、B独立，且P(A)>0  P(B|A)=P(B)  则：P(B|A)=P(AB)/P(A)=P(A)P(B)/P(A)=P(B) 

2. 若A、B独立，则A与𝐵 、𝐴 与B、 𝐴 与𝐵 也相互独立