二叉查找树

二叉查找树

定义： 二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 它的左、右子树也分别二叉排序树。

 

java实现二叉查找树节点的定义

private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

二叉查找树的实现

public class BST<E extends Comparable<E>> {
    //因为需要对节点进行比较，所以接受的泛型必须实现Comparable<E>
    private Node root;
    private int size;

    public BST() {
        this.root = null;
        this.size = 0;
    }

    public int getSize() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }
}

添加元素到二叉查找树

private Node add(Node node, E e) {
　　 //这里使用递归的方式来实现
    if (node == null) {
        size++;
        return new Node(e);
    }

    if (e.compareTo(node.e) < 0) {
        node.left = add(node.left, e);
    } else if (e.compareTo(node.e) > 0) {
        node.right = add(node.right, e);
    }

    return node;
}

判断二叉查找树是否包含元素

private boolean contains(Node node, E e) {
    if (node.e == null) {
        return false;
    }

    if (e.compareTo(node.e) < 0) {
        return contains(node.left, e);
    } else if (e.compareTo(node.e) > 0) {
        return contains(node.right, e);
    } else { //e.compareTo(node.e) == 0
        return true;
    }
}

前序遍历

• 递归实现（递归的方式很好实现，还好理解。如果对于性能要求不高的话，可以选择递归）

/**
 * 二分搜索树前序遍历-----递归实现
 * @param node
 */
private void preOrder(Node node) {
    if (node == null) {
        return;
    }

    System.out.println(node.e);//遍历根节点
    preOrder(node.left);
    preOrder(node.right);
}

 

• 非递归实现（非递归的方式相比递归的话，比较不好实现和理解。性能方面比较好）

/**
 * 二分搜索树前序遍历-----非递归实现
 */
public void proOrderNR() {
    Stack<Node> stack = new Stack<>();

    stack.push(root);
    while (!stack.isEmpty()) {
        Node cur = stack.pop();
        System.out.println(cur.e);//遍历根节点

        if (cur.right != null)
            stack.push(cur.right);
        if (cur.left != null)
            stack.push(cur.left);
    }
}

中序遍历

• 递归实现（递归的方式实现前中后三种遍历，仅仅只需要改动对左右子树递归的顺序即可，所以这里再给出中序遍历后就不给出后序遍历的递归实现了）

/**
 * 二分搜索树中序遍历-----递归实现
 * @param node
 */
private void inOrder(Node node) {
    if (node == null) {
        return;
    }

    inOrder(node.left);        //相比于前序遍历
    System.out.println(node.e);//只需要改变遍历的顺序，就可以实现中序遍历了
    inOrder(node.right);
}

 

• 非递归实现

/**
 * 二分搜索树中序遍历-----非递归实现
 */
public void inOrderNR() {

    Stack<Node> stack = new Stack<>();
    Node cur = root;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            //  ***
            stack.push(cur);//这是第一次碰到节点
            cur = cur.left;
        }
        cur = stack.pop();
        System.out.println(cur.e);//这是第二次碰到，将这条语句放在第一次碰到之前，
                                //函数就变成了前序遍历
        cur = cur.right;
    }
}

 

后序遍历

 

• 非递归实现

/**
 * 二分搜索树后序遍历-----非递归实现
 */
public void laterOrderNR() {

    Stack<Node> stack = new Stack<>();
    Node cur = root;
    Node right_cur = null;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        cur = stack.pop();
        // 当前结点没有右结点或上一个已经输出的结点是当前结点的右结点，则输出当前结点
        while (cur.right == null || cur.right == right_cur) {
            System.out.println(cur.e);
            right_cur = cur;
            if (stack.isEmpty()) {
                return; //root已输出，则遍历结束
            }
            cur = stack.pop();
        }
        stack.push(cur); //还有右结点没有遍历
        cur = cur.right;
    }
}

 

层序遍历

/**
   * 层序遍历
   */
  public void levelOrder(){
      Queue<Node> q = new LinkedList<>();
      q.add(root);
      while (!q.isEmpty()){
          Node cur = q.remove();
          System.out.println(cur.e);
  
          if (cur.left!=null)
              q.add(cur.left);
  
          if (cur.right!=null)
              q.add(cur.right);
  
      }
  }

查找最大和小元素

因为二分搜索树的性质，最小元素就是根节点向左子树遍历，遍历到最后的那个节点。相反的最大元素就是从根节点向右子树遍历，遍历到最后的节点。

//查找最小的元素，这里给出递归的方式
public E minFind() {
    if (size == 0) {
        throw new IllegalArgumentException("BST is empty!");
    }
    return minFind(root).e;
}

private Node minFind(Node node) {

    if (node.left == null) {
        return node;
    }
    return minFind(node.left);
}
//查找最大的元素
public E maxFind() {
    if (size == 0) {
        throw new IllegalArgumentException("BST is empty!");
    }
    return maxFind(root).e;
}

private Node maxFind(Node node) {

    if (node.right == null) {
        return node;
    }
    return maxFind(node.right);
}

 

 

删除最小元素

public E removeMin() {
    E res = minFind();
    root = removeMin(root);
    return res;
}

//删除以node为根的二叉搜索树的最小节点
//返回删除节点后新的二叉树的根
private Node removeMin(Node node) {
    if (node.left == null) {
        Node rightNode = node.right;
        node.right = null;
        size--;
        return rightNode;
    }
    node.left = removeMin(node.left);
    return node;
}

删除最大元素逻辑和删除最小元素一样，这里就不再给出了。

删除任意元素

删除元素这里要分情况讨论一下

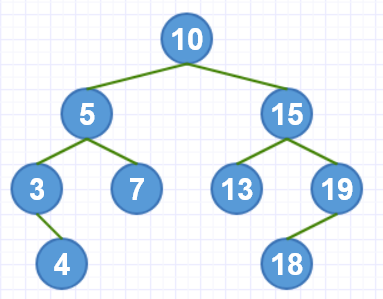
• 删除的是叶子节点，像上面的4、7、13 、18这样的没有左右子树的节点。

  　　　这种情况下，直接删除就可以了。

• 删除的节点只有左子树或右子树，像3 、 19

       　  这种情况只需要把要删除的节点的子树替代待删除节点的位置就可以。如：4代替3的位置，18代替19的位置

• 删除的节点有左右子树，像10、5 、15.

             这种的话需要把待删除的节点的右子树中的最小节点替换到待删除节点的位置，或者把待删除的节点的左子树中的最大节点替换到待删除节点的位置，也就是把待删除节点的后继节点或前驱节点代替被删除节点。如：要删除10这个节点，可以把13或者7移到10的位置。

public void remove(E e) {
    root = remove(root, e);
}
//这里也是递归实现的，非递归的方式以后会补上
//删除值为e以node为根的二叉搜索树的节点
//返回删除节点后新的二叉树的根
private Node remove(Node node, E e) {
    if (node == null) {
        return null;
    }
    
    if (e.compareTo(node.e) < 0) {
        node.left = remove(node.left, e);
        return node;
    } else if (e.compareTo(node.e) > 0) {
        node.right = remove(node.right, e);
        return node;
    } else { //e==node.e
        //待删除节点左子树为空
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        //待删除节点右子树为空
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }
        //待删除节点左右节点都不为空
        //找到比待删除节点大的最小节点
        //用这个节点替换待删除的节点，实现删除
        Node successor = minFind(node.right);
        successor.right = removeMin(node.right);
        successor.left = node.left;
        node.left = node.right = null;
        return successor;
    }
}