Python小白的数学建模课-12.非线性规划


  • 非线性规划是指目标函数或约束条件中包含非线性函数的规划问题，实际就是非线性最优化问题。
  • 从线性规划到非线性规划，不仅是数学方法的差异，更是解决问题的思想方法的转变。
  • 非线性规划问题没有统一的通用方法，我们在这里学习的当然不是数学方法，而是如何建模、如何编程求解。
  • 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

1. 从线性规划到非线性规划

本系列的开篇我们介绍了线性规划 （Linear Programming） 并延伸到整数规划、0-1规划，以及相对复杂的固定费用问题、选址问题。这些问题的共同特点是，目标函数与约束条件都是线性函数。如果目标函数或约束条件中包含非线性函数，则是非线性规划。

通常，非线性问题都比线性问题复杂得多，困难得多，非线性规划也是这样。非线性规划没有统一的通用方法、算法来解决，各种方法都有特定的应用范围和适用条件。另一方面，很多非线性规划问题在实践中不能获得全局最优解，只能得到局部最优解或近似最优解。

这意味着什么？对于数学研究来说，这也许意味着存在新的课题和挑战，可以研究更有效的算法。确实如此，即便线性规划问题的研究也在不断前进，非线性规划问题的研究更是丰富多彩。但热闹是他们的，我什么也没有。

我所想到的，是数学建模学习/课程/竞赛的根本目的是什么？是掌握各种算法的推演，努力编程以实现，还是练习分析问题建立模型的能力，使用软件和工具求解问题的能力？显然是后者。可是，为什么培训课上老师讲的都是算法呢？到了例题例程，不是一带而过，就是跳步骤讲。听课时津津有味，下课了题目还是不会做，程序还是调不通。于是，...

不过，到了非线性规划这一课，我们发现老师也不再不厌其烦地讲算法了，不知道是讲不下去还是讲不过来了： 20世纪50年代，H.W.Kuhn 和 A.W.Tucker 提出了非线性规划的基本定理，为非线性规划奠定了理论基础 ；50、60 年代出现了许多解非线性规划问题的有效算法；80年代后，随着计算机技术的快速发展，非线性规划方法取得了长足进步，在信赖域法、稀疏拟牛顿法、并行计算、内点法和有限存储法等领域取得了丰硕的成果。

所以，没关系的，都一样——参见章北海文集。

这意味着什么呢？这意味着对于学习数学建模的小白，学会把问题简化为非线性规划的标准方程，学会按照本文的方法使用求解工具包的函数，才能求解非线性规划问题，才能完赛。


2. Scipy 库求解非线性规划问题

2.1 非线性规划问题的描述

首先，我们回顾线性规划问题的标准形式：

\[\begin{align} & min\;f(x) = \sum_{j=1} ^n c_j x_j\\ & s.t.:\begin{cases} \sum_{j=1} ^n a_{ij} x_j = b_i, \\ x_j \geq 0 \end{cases} \end{align} \]

类似地，可以写出非线性规划的一般形式：

\[\begin{align} & min\;f(x) \\ & s.t.:\begin{cases} h_j(x) \leq 0, &j=1,q\\ g_i(x) = 0, &i=1,p \end{cases} \end{align} \]

其中：\(x=[x_1,...,x_n]^T\) 为决策变量，\(f(x)\) 为目标函数，\(h_j(x)\) 和 \(g_i(x)\) 为约束条件。

由此可见，非线性规划问题，实际上就是带有约束条件的非线性函数优化问题。

按照我们的学习模式，非线性规划问题的建模和求解与线性规划问题是类似的，按照以下步骤进行：

  1. 问题定义，确定决策变量、目标函数和约束条件；
  2. 模型构建，由问题描述建立数学方程，并转化为标准形式的数学模型；
  3. 模型求解，用标准模型的优化算法对模型求解，得到优化结果。

2.2 Scipy 求解非线性规划问题的函数

Scipy 是 Python 算法库和数学工具包，包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。

本文推荐和讲解使用 Scipy 工具包中的 optimize 模块求解常见的非线性规划问题。

scipy.optimize 模块中提供了多个用于非线性规划问题的方法，适用于不同类型的问题。

  • brent()：单变量无约束优化问题，混合使用牛顿法/二分法。

  • fmin()：多变量无约束优化问题，使用单纯性法，只需要利用函数值，不需要函数的导数或二阶导数。

  • leatsq()：非线性最小二乘问题，用于求解非线性最小二乘拟合问题。

  • minimize()：约束优化问题，使用拉格朗日乘子法将约束优化转化为无约束优化问题。


2.3 scipy.optimize.brent() 求解单变量无约束优化问题

非线性规划最简单的形式是一维搜索，一维搜索的常用方法是函数逼近法和区间收缩法。

brent() 函数是 SciPy.optimize 模块中求解单变量无约束优化问题最小值的首选方法。这是牛顿法和二分法的混合方法，既能保证稳定性又能快速收敛。

scipy.optimize.brent(func, args=(), brack=None, tol=1.48e-08, full_output=0, maxiter=500)

optimize.brent() 的主要参数：

  • func: callable f(x,*args) 　　目标函数 \(f(x)\)，以函数形式表示，可以通过 *args 传递参数
  • args: tuple　　可选项，以 f(x,*args) 的形式将可变参数 p 传递给目标函数 \(f(x,p)\) 。
  • brack: tuple　　可选项，搜索算法的开始区间（不是指 x 的上下限）

optimize.brent() 的主要返回值：

  • **xmin: ** 　　返回函数达到最小值时的 x（注意是局部最优，不一定是全局最优）。
  • **fval: ** 　　返回函数的最优值（默认不返回，仅当 full_output 为 1 时返回）。

optimize.brent() 的使用例程：

from scipy.optimize import brent, fmin_ncg, minimize
import numpy as np

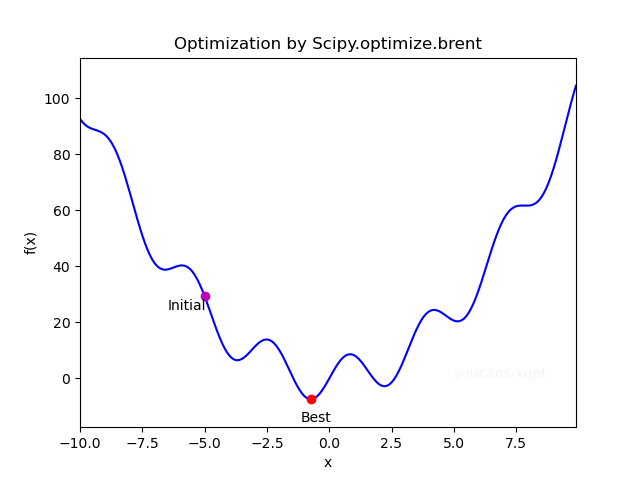
# 1. Demo1：单变量无约束优化问题(Scipy.optimize.brent)
def objf(x):  # 目标函数
    fx = x**2 - 8*np.sin(2*x+np.pi)
    return fx

xIni = -5.0
xOpt= brent(objf, brack=(xIni,2))
print("xIni={:.4f}\tfxIni={:.4f}".format(xIni,objf(xIni))
print("xOpt={:.4f}\tfxOpt={:.4f}".format(xOpt,objf(xOpt)))

例程运行结果：

xIni=-5.0000	fxIni=29.3522
xOpt=-0.7391	fxOpt=-7.4195


2.4 scipy.optimize.fmin() 求解多变量无约束优化问题

多变量无约束优化问题的算法很多，分类方式也很多。从使用者的角度来说可以分为：只使用目标函数值、使用导数（梯度下降法）、使用二阶导数。大体来说，使用导数的算法收敛较快，使用二阶导数收敛更快，但是收敛快也容易陷入局部最优。

fmin() 函数是 SciPy.optimize 模块中求解多变量无约束优化问题（最小值）的首选方法，采用下山单纯性方法。下山单纯性方法又称 Nelder-Mead 法，只使用目标函数值，不需要导数或二阶导数值，是最重要的多维无约束优化问题数值方法之一。

scipy.optimize.fmin(func, x0, args=(), xtol=0.0001, ftol=0.0001, maxiter=None, maxfun=None, full_output=0, disp=1, retall=0, callback=None, initial_simplex=None)

optimize.fmin() 的主要参数：

  • func: callable f(x,*args) 　　目标函数 \(f(x)\)，以函数形式表示，可以通过 *args 传递参数。
  • x0: nadarray　　搜索算法的初值。
  • args: tuple　　可选项，以 f(x,*args) 的形式将可变参数 p 传递给目标函数 \(f(x,p)\) 。

optimize.fmin() 的主要返回值：

  • **xopt: ** 　　返回最小值时的 x 值。
  • **fopt: ** 　　返回最小值时的目标函数值，fopt=func(xopt)。

optimize.fmin() 的使用例程：

from scipy.optimize import brent, fmin, minimize
import numpy as np

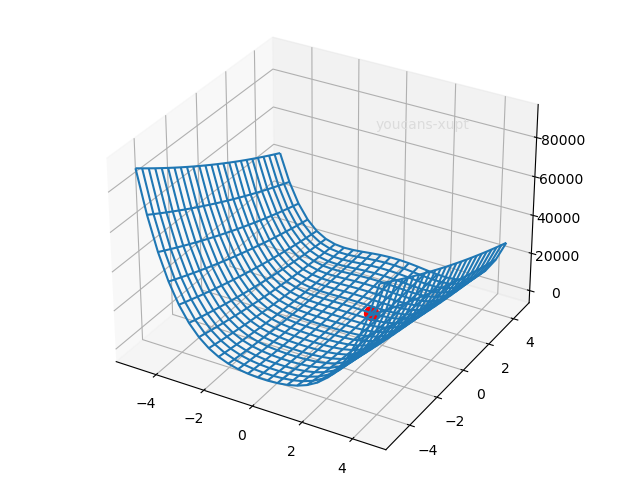
# 2. Demo2：多变量无约束优化问题(Scipy.optimize.brent)
# Rosenbrock 测试函数
def objf2(x):  # Rosenbrock benchmark function
    fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
    return fx

xIni = np.array([-2, -2])
xOpt = fmin(objf2, xIni)
print("xIni={:.4f},{:.4f}\tfxIni={:.4f}".format(xIni[0],xIni[1],objf2(xIni)))
print("xOpt={:.4f},{:.4f}\tfxOpt={:.4f}".format(xOpt[0],xOpt[1],objf2(xOpt)))

例程运行结果：

xIni=-2.0000,-2.0000	fxIni=3609.0000
xOpt=1.0000,1.0000		fxOpt=0.0000


3. scipy.optimize.minimize() 求解非线性规划问题

3.1 scipy.optimize.minimize() 函数说明

minimize() 函数是 SciPy.optimize 模块中求解多变量优化问题的通用方法，可以调用多种算法，支持约束优化和无约束优化。

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

optimize.minimize() 的主要参数：

  • fun: callable f(x,*args) 　　目标函数 \(f(x)\)，以函数形式表示，可以通过 *args 传递参数。
  • x0: nadarray, shape(n,)　　搜索算法的初值，n 是决策变量个数。
  • args: tuple　　可选项，将可变参数传递给目标函数 fun、导数函数 jac 和二阶导数函数 hess。
  • method: str　　可选项，选择优化算法。默认算法为 BFGS, L-BFGS-B, SLSQP（取决于问题有没有边界条件和约束条件）
  • **jac: **　　可选项，梯度计算方法。可以以函数形式表示，或选择 '2-point', '3-point', 'cs'。该选项只能用于 CG, BFGS, Newton-CG, L-BFGS-B, TNC, SLSQP, dogleg, trust-ncg, trust-krylov, trust-exact 和 trust-constr 算法。
  • **hess: **　　可选项，Hessian 矩阵计算方法。可以以函数形式表示，或选择 '2-point', '3-point', 'cs'。该选项只能用于 Newton-CG, dogleg, trust-ncg, trust-krylov, trust-exact 和 trust-constr 算法。
  • **bounds: **　　可选项，变量的边界条件（上下限，lb<=x<=ub）。该选项只能用于 Nelder-Mead, L-BFGS-B, TNC, SLSQP, Powell 和 trust-constr 算法。
  • **constraints: **　　可选项，定义约束条件 f(x)>=0。该选项只能用于 COBYLA, SLSQP 和 trust-constr 算法，注意不同算法中对于约束条件的定义是不同的。

optimize.minimize() 的主要返回值：

  • **res: ** 　　返回优化结果，以对象方式表示，主要包括优化是否成功、决策变量的优化值 xOpt。

optimize.minimize() 的优化算法选项：

optimize.minimize() 的默认算法为 BFGS, L-BFGS-B, SLSQP（取决于问题有没有边界条件和约束条件），可以通过 "method=None" 选项调用多种算法：

无约束问题优化算法

  • **method=‘CG’ **：　　非线性共轭梯度算法，只能处理无约束优化问题，需要使用一阶导数函数。

  • **method=‘BFGS’ **：　　BFGS 拟牛顿法，只能处理无约束优化问题，需要使用一阶导数函数。BFGS 算法性能良好，是无约束优化问题的默认算法。

  • **method=‘Newton-CG’ **：　　截断牛顿法，只能处理无约束优化问题，需要使用一阶导数函数，适合处理大规模问题。

  • **method=‘dogleg’ **：　　dog-leg 信赖域算法，需要使用梯度和 Hessian（必须正定），只能处理无约束优化问题，

  • **method=‘trust-ncg’ **：　　采用牛顿共轭梯度信赖域算法，需要使用梯度和 Hessian（必须正定），只能处理无约束优化问题，适合大规模问题。

  • method=‘trust-exact’：　　求解无约束极小化问题的信赖域方法，需要梯度和Hessian（不需要正定）。

  • method=‘trust-krylov’：　　使用Newton-GLTR 信赖域算法度，需要使用梯度和 Hessian（必须正定），只能处理无约束优化问题，适合中大规模问题。

边界约束条件问题优化算法

  • method=‘Nelder-Mead’：　　下山单纯性法，可以处理边界约束条件（决策变量的上下限），只使用目标函数，不使用导数函数、二阶导数，鲁棒性强。

  • **method=‘L-BFGS-B’ **：　　改进的 BFGS 拟牛顿法，L- 指有限内存，-B 指边界约束，可以处理边界约束条件，需要使用一阶导数函数。L-BFGS_B 算法性能良好，消耗内存量很小，适合处理大规模问题，是边界约束优化问题的默认算法。

  • method=‘Powell’：　　改进的共轭方向法，可以处理边界约束条件（决策变量的上下限）。

  • **method=‘TNC’ **：　　截断牛顿法，可以处理边界约束条件

带有约束条件问题优化算法

  • **method=‘COBYLA’ **：　　线性近似约束优化方法，通过对目标函数和约束条件的线性逼近处理非线性问题。只使用目标函数，不需要导数或二阶导数值，可以处理约束条件。

  • **method=‘SLSQP’ **：　　序贯最小二乘规划算法，可以处理边界约束、等式约束和不等式约束条件。SLSQP 算法性能良好，是带有约束条件优化问题的默认算法。

  • **method=‘trust-constr’ **：　　信赖域算法，通用的约束最优化方法，适合处理大规模问题。

由于 optimize.minimize() 实际是多种算法的集成接口，各种算法对于问题、约束条件和参数的定义并不完全相同，对于各种算法的研究和应用已超出本文的内容，有兴趣的读者可以阅读官方文档： scipy.optimize.minimize — SciPy v1.7.0 Manual
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize

我们还是针对数学建模的常用需求和小白的特点，结合实际案例来学习基本应用。


3.2 scipy.optimize.minimize() 函数使用例程

编程步骤说明：

  1. 导入 scipy、numpy 包；
  2. 定义目标函数 objf3(x)，输入变量 x 表示向量，返回值 fx 是目标函数的计算结果 。
  3. 定义边界约束，即优化变量的上下限：
    • minimize() 默认无边界约束条件，即各自变量的取值范围没有限制；
    • 如果设置边界约束，要对每个自变量（决策变量）定义其上下限，注意定义边界约束的格式；
    • 如果某个自变量没有上限（下限），则表示为 None 。
  4. 定义 x 的初值。
  5. 求解最小化问题 resRosen，其中目标函数 objf3 和搜索的初值点 xIni 是必需的，指定优化方法和边界条件是可选项。如果优化问题是求最大值 maxFx，可以通过 minFx = - maxFx 的变换来实现。
  6. 通过调用最小化问题的返回值 resRosen.x 得到最优点 xOpt。

Python 例程：

from scipy.optimize import brent, fmin, minimize
import numpy as np

# 3. Demo3：多变量边界约束优化问题(Scipy.optimize.minimize)
# 定义目标函数
def objf3(x):  # Rosenbrock 测试函数
    fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
    return fx

# 定义边界约束（优化变量的上下限）
b0 = (0.0, None)  # 0.0 <= x[0] <= Inf
b1 = (0.0, 10.0)  # 0.0 <= x[1] <= 10.0
b2 = (-5.0, 100.)  # -5.0 <= x[2] <= 100.0
bnds = (b0, b1, b2)  # 边界约束

# 优化计算
xIni = np.array([1., 2., 3.])
resRosen = minimize(objf3, xIni, method='SLSQP', bounds=bnds)
xOpt = resRosen.x

print("xOpt = {:.4f}, {:.4f}, {:.4f}".format(xOpt[0],xOpt[1],xOpt[2]))
print("min f(x) = {:.4f}".format(objf3(xOpt)))

例程运行结果：

xOpt = 1.0000, 1.0000, 1.0000
min f(x) = 0.0000

4. 约束非线性规划问题实例

4.1 非线性规划问题的数学模型：

\[\begin{align} & min\;f(x) = a*x_1^2 + b*x_2^2 + c*x_3^2 + d\\ & s.t.:\begin{cases} x_1^2 - x_2 + x_3^2 \geq 0\\ x_1 + x_2^2 + x_3^3 \leq 20\\ -x_1 - x_2^2 + 2 = 0\\ x_2 + 2x_3^2 = 3\\ x_1, x_2, x_3 \geq 0 \end{cases} \end{align} \]

由于 minimize() 函数中对约束条件的形式定义为 f(x)>=0，因此要将问题的数学模型转换为标准形式：

\[\begin{align} & min\;f(x) = a*x_1^2 + b*x_2^2 + c*x_3^2 + d\\ & s.t.:\begin{cases} x_1^2 - x_2 + x_3^2 \geq 0 \\ -(x_1 + x_2^2 + x_3^3 - 20) \geq 0 \\ -x_1 - x_2^2 + 2 = 0 \\ x_2 + 2x_3^2 - 3 = 0 \\ x_1, x_2, x_3 \geq 0 \end{cases} \end{align} \]


4.2 Python 例程 1：

程序说明：

  1. 在本例程中，目标函数中的参数 a, b, c, d 在子程序中直接赋值，这种实现方式最简单；
  2. 定义边界约束，即优化变量的上下限，与 3.2 中的例程相同，用 minimize() 函数中的选项 bounds=bnds 进行定义。
  3. 定义约束条件：
    • 本案例有 4个约束条件，2个等式约束、2个不等式约束，上节中已写成标准形式；
    • 本例程将每个约束条件作为一个子函数定义，
    • minimize() 函数对约束条件按照字典格式： {'type': 'ineq', 'fun': functionname} 进行定义。'type' 的键值可选 'eq' 和 'ineq'，分别表示的是约束和不等式约束；functionname是定义约束条件的函数名。
  4. 求解最小化问题 res，其中目标函数 objF4 和搜索的初值点 x0 是必需的，指定优化方法和边界条件、约束条件是可选项。
  5. 通过调用最小化问题的返回值可以得到优化是否成功的说明（res.message）、自变量的优化值（res.x）和目标函数的优化值（res.fun）。

Python 例程：

from scipy.optimize import brent, fmin, minimize
import numpy as np

# 4. Demo4：约束非线性规划问题(Scipy.optimize.minimize)
def objF4(x):  # 定义目标函数
    a, b, c, d = 1, 2, 3, 8
    fx = a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
    return fx

# 定义约束条件函数
def constraint1(x):  # 不等式约束 f(x)>=0
    return x[0]** 2 - x[1] + x[2]**2
def constraint2(x):  # 不等式约束 转换为标准形式
    return -(x[0] + x[1]**2 + x[2]**3 - 20)
def constraint3(x):  # 等式约束
    return -x[0] - x[1]**2 + 2
def constraint4(x):  # 等式约束
    return x[1] + 2*x[2]**2 -3

# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)

# 定义约束条件
con1 = {'type': 'ineq', 'fun': constraint1}
con2 = {'type': 'ineq', 'fun': constraint2}
con3 = {'type': 'eq', 'fun': constraint3}
con4 = {'type': 'eq', 'fun': constraint4}
cons = ([con1, con2, con3,con4])  # 3个约束条件

# 求解优化问题
x0 = np.array([1., 2., 3.])  # 定义搜索的初值
res = minimize(objF4, x0, method='SLSQP', bounds=bnds, constraints=cons)

print("Optimization problem (res):\t{}".format(res.message))  # 优化是否成功
print("xOpt = {}".format(res.x))  # 自变量的优化值
print("min f(x) = {:.4f}".format(res.fun))  # 目标函数的优化值

例程 1 运行结果：

Optimization problem (res):	Optimization terminated successfully
xOpt = [0.6743061  1.15138781 0.96140839]
min f(x) = 13.8790

4.3 Python 例程 2：

程序说明：

  1. 本例程的问题与 4.2 中的例程 1 是相同的，结果也相同，但编程实现的方法进行了改进；

  2. 本例程中目标函数中的参数 a, b, c, d 在主程序中赋值，通过 args 把参数传递到子程序，这种实现方式使参数赋值更为灵活，特别是适用于可变参数的问题；注意目标函数的定义不是 def objF5(x,args)，而是 def objF5(args)，要特别注意目标函数的定义和实现方法。

  3. 定义约束条件：

    • 本案例有 4 个约束条件，2个等式约束、2个不等式约束，上节中已写成标准形式；
    • 本例程将 4 个约束条件放在一个子函数中定义，是程序更加简洁。
    • 注意每个约束条件仍然按照字典格式 {'type': 'ineq', 'fun': functionname} 进行定义，但 functionname 并不是函数名，而是一个 lambda 匿名函数。

  4. 通过调用最小化问题的返回值可以得到优化是否成功的说明（res.message）、自变量的优化值（res.x）和目标函数的优化值（res.fun）。

Python 例程 2：

from scipy.optimize import brent, fmin, minimize
import numpy as np

# 5. Demo5：约束非线性规划问题(Scipy.optimize.minimize)
def objF5(args):  # 定义目标函数
    a,b,c,d = args
    fx = lambda x: a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
    return fx

def constraint1():  # 定义约束条件函数
    cons = ({'type': 'ineq', 'fun': lambda x: (x[0]**2 - x[1] + x[2]**2)},  # 不等式约束 f(x)>=0
            {'type': 'ineq', 'fun': lambda x: -(x[0] + x[1]**2 + x[2]**3 - 20)},  # 不等式约束 转换为标准形式
            {'type': 'eq', 'fun': lambda x: (-x[0] - x[1]**2 + 2)},  # 等式约束
            {'type': 'eq', 'fun': lambda x: (x[1] + 2*x[2]**2 - 3)})  # 等式约束
    return cons

# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)
# 定义约束条件
cons = constraint1()
args1 = (1,2,3,8)  # 定义目标函数中的参数
# 求解优化问题
x0 = np.array([1., 2., 3.])  # 定义搜索的初值
res1 = minimize(objF5(args1), x0, method='SLSQP', bounds=bnds, constraints=cons)

print("Optimization problem (res1):\t{}".format(res1.message))  # 优化是否成功
print("xOpt = {}".format(res1.x))  # 自变量的优化值
print("min f(x) = {:.4f}".format(res1.fun))  # 目标函数的优化值

例程 2 运行结果：

Optimization problem (res1):	Optimization terminated successfully
xOpt = [0.6743061  1.15138781 0.96140839]
min f(x) = 13.8790

4.4 Python 例程 3：

程序说明：

  1. 本例程的问题与 4.3 中的例程 2 是相同的，结果也相同，但编程实现的方法进行了改进；
  2. 本例程中约束条件中的参数在主程序中赋值，通过 args 把参数传递到约束条件定义的子程序，这种实现方式使参数赋值更为灵活，特别是适用于可变参数的问题。
  3. 本例程中将边界约束条件即自变量的取值范围作为不等式约束条件处理，不另作边界条件设置。
  4. 通过调用最小化问题的返回值可以得到优化是否成功的说明（res.message）、自变量的优化值（res.x）和目标函数的优化值（res.fun）。

Python 例程 3：

from scipy.optimize import brent, fmin, minimize
import numpy as np

# 6. Demo6：约束非线性规划问题(Scipy.optimize.minimize)
def objF6(args):  # 定义目标函数
    a,b,c,d = args
    fx = lambda x: a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
    return fx

def constraint2(args):
    xmin0, xmin1, xmin2 = args
    cons = ({'type': 'ineq', 'fun': lambda x: (x[0]**2 - x[1] + x[2]**2)},  # 不等式约束 f(x)>=0
            {'type': 'ineq', 'fun': lambda x: -(x[0] + x[1]**2 + x[2]**3 - 20)},  # 不等式约束 转换为标准形式
            {'type': 'eq', 'fun': lambda x: (-x[0] - x[1]**2 + 2)},  # 等式约束
            {'type': 'eq', 'fun': lambda x: (x[1] + 2*x[2]**2 - 3)},  # 等式约束
            {'type': 'ineq', 'fun': lambda x: (x[0] - xmin0)},  # x0 >= xmin0
            {'type': 'ineq', 'fun': lambda x: (x[1] - xmin1)},  # x1 >= xmin1
            {'type': 'ineq', 'fun': lambda x: (x[2] - xmin2)})  # x2 >= xmin2
    return cons

# 求解优化问题
args1 = (1,2,3,8)  # 定义目标函数中的参数
args2 = (0.0, 0.0, 0.0)  # xmin0, xmin1, xmin2
cons2 = constraint2(args2)

x0 = np.array([1., 2., 3.])  # 定义搜索的初值
res2 = minimize(objF6(args1), x0, method='SLSQP', constraints=cons2)

print("Optimization problem (res2):\t{}".format(res2.message))  # 优化是否成功
print("xOpt = {}".format(res2.x))  # 自变量的优化值
print("min f(x) = {:.4f}".format(res2.fun))  # 目标函数的优化值

例程 3 运行结果：

Optimization problem (res2):	Optimization terminated successfully
xOpt = [0.6743061  1.15138781 0.96140839]
min f(x) = 13.8790

5. 小结

Scipy 工具包中的 minimize() 函数集成了多种求解线性规划问题的算法，可以处理边界条件和等式、不等式约束，对于常见的非线性规划问题都能获得较好的解。

minimize() 函数对于等式约束、不等式约束条件的编程定义了标准形式和输入格式，通过对比 4.2～4.4 的 3个例程可以帮助读者理解有关的格式要求。

【本节完】


版权说明：

欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品

CSDN 原创作品，转载必须标注原文链接：(https://www.cnblogs.com/youcans/p/15064686.html)。

Copyright 2021 Youcans, XUPT

Crated：2021-06-30


欢迎关注 『Python小白的数学建模课 @ Youcans』，每周更新数模笔记
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-10.微分方程边值问题
Python小白的数学建模课-B2.新冠疫情 SI模型
Python小白的数学建模课-B3.新冠疫情 SIS模型
Python小白的数学建模课-B4.新冠疫情 SIR模型
Python小白的数学建模课-B5.新冠疫情 SEIR模型
Python小白的数学建模课-B6.改进 SEIR疫情模型

posted @ 2021-07-27 10:50  youcans  阅读(4610)  评论(1)  编辑  收藏  举报