[OI笔记]基础图论/图算法

• [2017.8.29 00:00]——前几天开始好好学了几天的图论，不过这最近又突然因为一些原因（其实是晚上没睡好导致白天没精神）颓废了几天…一方面为了控制自己同时也可以当做之后noip前复习用的笔记，毕竟自学党的笔记只能这样子了吧。嗯，尽量写一些比较有用的东西以后自己方便复习也方便给新人看（我自己不还是新人么x），除了图算法其他一些内容之后学到也尽量开个博客记一下…嗯大概就这样
• 不定期更新
• 如有错误还请指出！
• 其实主要是留给自己用的，如果想要好好学的话还是去找比较具体的blog吧

---

想写的东西（大部分只留代码）：

• 图的表示/储存/访问
• 强连通分量
• 求最小生成树的的两种算法（K开头的那啥Kruskal跟Prim）
• 单源最短路算法（Dij什么什么的和SPFA（Bellman-Ford队列优化））和多源最短路算法（Floyd）
• 图的割点
• 双联通分量（这个暂时还不会QAQ）
• 拓扑排序
• 欧拉路
• 网络流相关 （开玩笑我怎么可能会网络流QwQ）
• 一些基础的杂题

---

图的表示/储存/访问

---

• 参考文献：算法导论

（话说这部分会比较基础觉得没问题的可以直接跳下去）（目前下面还没有）
如果比较严格的，一般记图\(G\)为一个二元组\(G=(V,E)\)，其中\(V\)为有限集，称为图\(G\)的顶点集，\(V\)中的元素称为顶点。称为图\(G\)的边集，其元素称为边。两个顶点相同的边称为自环。对于有向图来说\(E\)由\(V\)中两个元素构成的二元关系，而无向图的边集\(E\)则是由无序的顶点对构成的，而不是有序对。
（下面还是不要用这么“严格”的说法好了，如果想看严格的说法可以参考算法导论
比如下图是一个顶点集为\(V=\{1,2,3,4,5,6\}\)边集为\(E=\{(1,1),(1,2),(1,3),(1,4),(2,4),(5,6),(6,5)\}\)的有向图的栗子

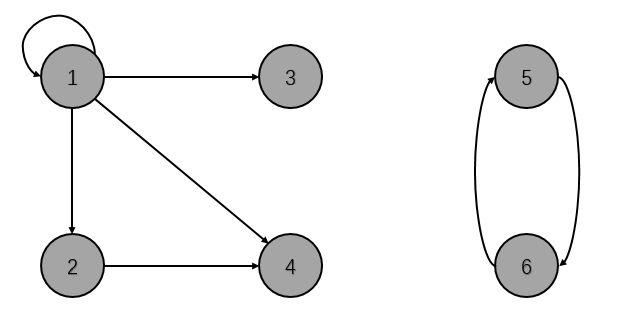
QwQ啊感觉这些概念不太好讲我也表达不清楚…概念部分就这样先过了吧x想了解的还是查其他的资料吧~
下面还是说说储存吧QwQ

我常用（或者可以说是用过的）的大概就两种…邻接矩阵和链式前向星，我邻接表好像不怎么用…

• 邻接矩阵：用一个矩阵\(A\)存图的边，比如可以用\(A[u][v]\)表示图中从\(u\)到\(v\)的一条边，边权就直接存在表中，不存在边一般就直接设为\(0\)，\(∞\)或者是一些特殊值（具体根据实际情况）。这种表示方法可以快速查找两个点之间是否有边，以及如果有那么这条边的边权是多少，但如果有重边的话可能不太好处理，空间复杂度是\(O(n^2)\)。（目前我好像除了写Floyd以外基本没有用邻接矩阵…

• 链式前向星：
  我们建一个结构体来表示权值为weight的边\((u,v)\)：

    struct edge{int v,weight,next;};
  

  next表示这条边的下一条边的储存位置
  \(u\)呢？往下看x
  边集数组直接：

    edge Edges[M];
  

  加边只要设一个全局变量比如cnt，表示当前到第几条边
  一个head[]数组表示以i为起点第一条边的位置
  然后加一条\(u\)到\(v\)的权值为\(w\)的边就直接：

    void addEdge(int u,int v,int w)
    {
        Edges[++cnt]=(edge){v,w,head[u]};
        head[u]=cnt;
    }
  

  然后注意其实这样子head[i]实际上是输入的i为起点的最后一条边，也就是反过来的，不过这在大多数情况下并不会对结果造成影响。（嘛反正我是没遇到过）

  如果需要遍历以cur为起点的所有边可以：

    for(int i=head[cur];i;i=Edges[i].next)
    {
        //
    }
  

  这样Edges[i]就是当前这条边了，你可以对她做任何事情
  然后这一部分大概就这样…
  最后强调四点需要注意的：

  • 加边注意顺序不要错（不要像我一样把w放到next把head[u]放到w里面233）
  • 无向图边集数组要开题目范围的两倍空间！
  • 无向图边集数组要开题目范围的两倍空间！！
  • 无向图边集数组要开题目范围的两倍空间！！！

---

强连通分量

---

大概就是有向图中如果任意两个点\(u\)和\(v\)互相可达，那么我们就称这个图为强连通图。有向图中一个极大的强连通子图就被称为强连通分量。
具体怎么求在这里不债述 （其实我也不怎么懂原理只会写模板）
有需要可以直接参考：BYVoid-有向图强连通分量的Tarjan算法

下面贴一下我平常的代码…大概长这样（临时打的不知道有没有打错…）

inline void tarjan(int i)
{
	int j;
	LOW[i]=DFN[i]=++Dindex;
	stack[++s_top]=i;
	inS[i]=1;
	for(int cur=head[i];cur;cur=edges[cur].next)
	{
		j=edges[cur].to;
		if(!DFN[j])
		{
			tarjan(j);
			LOW[i]=min(LOW[i],LOW[j]);
		}else if(inS[j])
			LOW[i]=min(LOW[i],DFN[j]);
	}
	if(DFN[i]==LOW[i])
	{
		++cntscc;
		do
		{
			j=stack[s_top]--;
			inS[j]=0;
			belong[j]=cntscc;
		}while(i!=j);
	}
}

（然后有没有人告诉我怎么证这个算法的正确性啊QAQ

---

丢一些模板先跑了x

---

因为开始正式上课了加上要准备开始学点新东西，剩下留着下次复习图论（如果有的话）再更吧
为了防止我老年痴呆症导致忘记怎么写一些模板…这里先贴几个模板（有空再来补充具体的说明）

丢模板逃x

---

如果有什么问题欢迎在评论区指出_(:з」∠)_