HDU6035-Colorful Tree-虚树思想

link：https://codeforces.com/gym/102253/problem/C
题意：一棵树，每个点有颜色，求所有路径上出现的颜色个数之和，基本要求线性。

---

对每种颜色考虑答案，枚举到颜色c的时候想着把所有颜色c的点拿出来，建立虚树，这样总的点数是 \(O(n)\) 的，但建虚树其实要 \(O(n\log n)\) 的时间，而且建完了的DP似乎也很麻烦。

对这个虚树考虑，如果颜色c用黑点表示，那么假设删去黑点，树会变成若干连通块，这个颜色的贡献就是 \(\binom{n}{2}-\sum_{block}\binom{sz}{2}\)

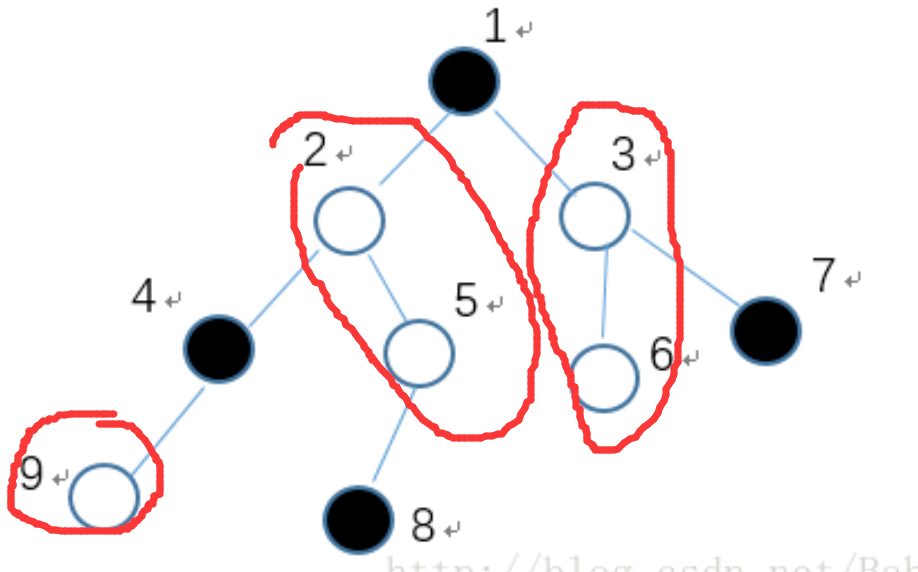
考虑从上往下模拟这个dfs的过程，对当前的结点x，对每个孩子结点 \(to\)，求出 \(sz[to]-\sum\) 从上往下\(c[x]\) 第一次出现的那些点的子树大小，就能确定对应的连通块大小，然后统计 \(x\) 的贡献。
这个子树大小可以通过一些类似树上差分的技巧完成：dfs时记录每种颜色当前还“剩下”几个点，一开始全部设为 \(n\) 个点，每次搜完某个 \(x\) ，就将其子树内的点全部删去——当然 \(x\) 内可能还会有 \(c[x]\) 颜色的其他点，稍微算一下差值就好

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define endl '\n'
#define fastio ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=2e5+5;
int n,c[N],sz[N],cnt[N];
vector<vector<int>> G;
ll ans;
ll C2(int n){return (ll)n*(n-1)/2;}
void dfs1(int x,int fa){
    sz[x]=1;
    for(auto to:G[x])if(to!=fa){
        dfs1(to,x);
        sz[x]+=sz[to];
    }
}
void dfs2(int x,int fa){
    if(x==1)rep(i,1,n)cnt[i]=n;
    int cur=cnt[c[x]];
    for(auto to:G[x])if(to!=fa){
        int before=cnt[c[x]];
        dfs2(to,x);
        int after=cnt[c[x]];
        int del=sz[to]-(before-after);
        ans+=C2(del);
        cnt[c[x]]-=del;
    }
    int lst=cnt[c[x]];
    cnt[c[x]]-=sz[x]-(cur-lst);
    if(x==1)rep(i,1,n)ans+=C2(cnt[i]);
}
int main(){
    fastio;
    int tc=0;
    while(cin>>n){
        tc++;
        rep(i,1,n)cin>>c[i];
        G=vector<vector<int>>(n+1);
        ans=0;
        rep(i,1,n-1){
            int u,v;
            cin>>u>>v;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dfs1(1,-1);
        dfs2(1,-1);
        cout<<"Case #"<<tc<<": "<<n*C2(n)-ans<<endl;
    }
    return 0;
}