CF1968E.Cells Arrangement-构造（给个和题解不同的做法）

link：https://codeforces.com/problemset/problem/1968/E
题意：需要构造一个 \(n\times n\) 的棋盘，在上面放 \(n\) 枚棋子，设集合 \(\mathcal{H}\) 表示两两之间曼哈顿距离构成的集合，要让 \(|\mathcal{H}|\) 最大。给出放棋子的方案。

---

首先说说题解的做法…考虑把距离为奇数和偶数的分开想…然后就会有下面这种，对角线放一堆，然后角落放两个的操作，非常合理…

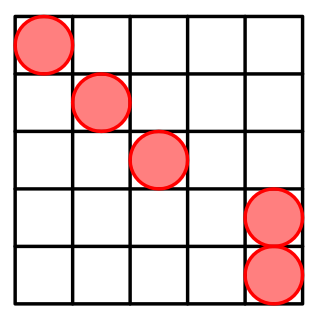
但是我完全没想到这么造…

首先想的是，距离最近是 \(0\)，最远是 \(2(n-1)=2n-2\)，答案上界应该是 \(2n-1\)，那我们就看看能不能取到上界，想这么一个构造：如果在左上角放了一排 \(L\) 个棋，可以得到 \([0,L-1]\) 的所有距离，至多可以造到 \([0,n-1]\)，这不够用

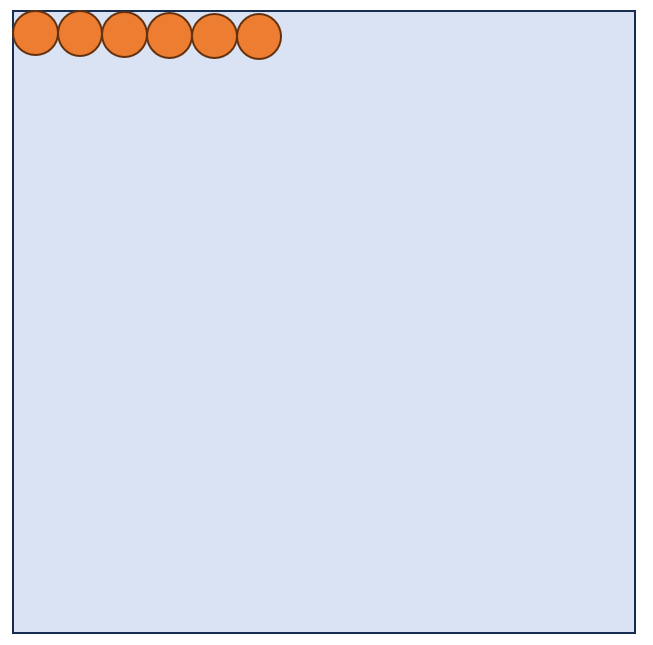
如果把棋盘分成四份，左上角放 \(n/2\) 个，右下角放一个，会发生什么呢？

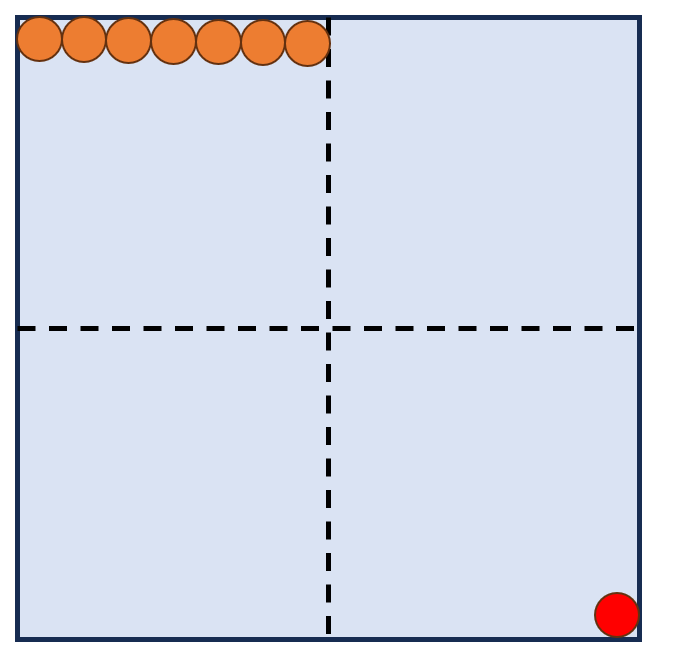
右下角能额外产生最小 \(n-1+(n/2)=\frac{3}{2} n-1\)，最大 \(2n-2\) 的值，这样是把 \([0,2n-2]\) 的前后都覆盖住了，中间还有大约 \(n\) 个数，再放几个球：

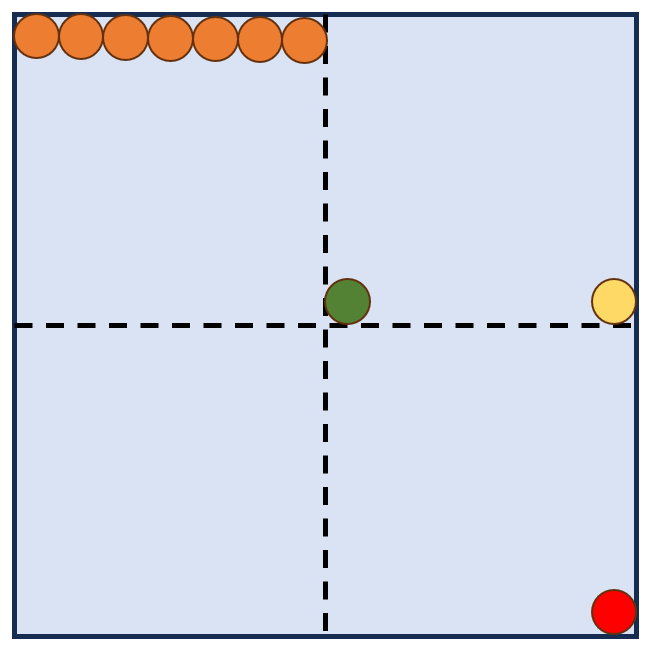
绿色小球和左上角能产生 \([n/2,n/2-1+n/2]=[n/2,n-1]\) 的值，而黄色小球能产生 \([n/2+n/2-1,n-1+(n/2-1)]=[n-1,\frac{3}{2}n-2]\) 的值。

所以大约用了 \(\frac{n}{2}+3\) 个球就得到了最大值…剩下的随便乱放就好。
当然，具体实现的时候wa了一发， \(n=4\) 的时候太小会出问题，其他情况都能取得到。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define endl '\n'
#define fastio ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
int main(){
    fastio;
    int tc;cin>>tc;
    while(tc--){
        int n;
        cin>>n;
        vector<pii> ans;
        int lst=n;
        if(n==4){
            ans.push_back({1,1});
            ans.push_back({1,3});
            ans.push_back({4,3});
            ans.push_back({4,4});
        }else{
            rep(i,1,(n+1)/2){
                ans.push_back({1,i});
                lst--;
            }
            ans.push_back({n,n});lst--;
            if(lst){
                ans.push_back({(n+1)/2,(n+1)/2+1});
                lst--;
            }
            if(lst){
                ans.push_back({(n+1)/2+1,n});
                lst--;
            }
            while(lst--)ans.push_back({n,n});
        }

        for(auto [x,y]:ans)cout<<x<<' '<<y<<endl;
        cout<<endl;
    }
    return 0;
}