洛谷2664树上游戏-点分治
link:https://www.luogu.com.cn/problem/P2664
lrb 有一棵树,树的每个节点有个颜色。给一个长度为 \(n\) 的颜色序列,定义 \(s(i,j)\) 为 \(i\) 到 \(j\) 的颜色数量。以及
\[sum_i=\sum_{j=1}^n s(i, j)
\]
现在他想让你求出所有的 \(sum_i\)。
一个暴力的想法:因为是求和,所以可以拆开算贡献。枚举每个颜色 \(c\),将颜色 \(c\) 的点拿出来,会把原树划分成若干个连通块,对每个点的贡献即为 \(n-sz_i\) ,其中 \(sz_i\) 表示 \(i\) 所属连通块大小。连通块用并查集维护,这样是 \(O(n^2)\)的。
考虑点分治,对于当前的分治中心 \(x\),需要考虑:
- 以 \(x\) 为某个端点,延伸到某个子节点的产生的答案。
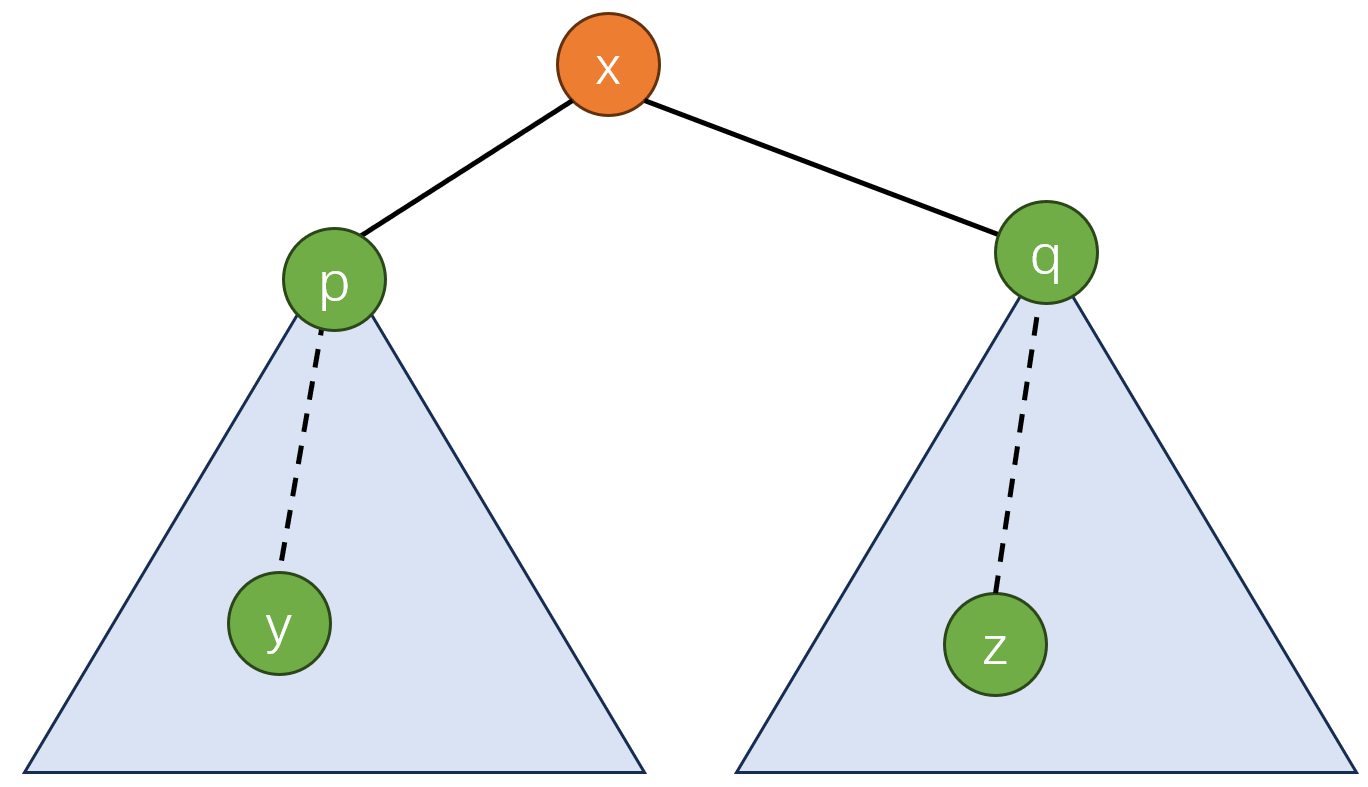
- 以 \(x\) 为LCA,从某个子树中的 \(y\) 出发(或直接从 \(x\) 出发)对另一子树中 \(z\) 的贡献。
第一种情况直接一次dfs统计:
void dfs1(int x,int fa,int from){
cnt_col[c[x]]++;
if(cnt_col[c[x]]==1)ans[from]+=sz[x];
for(auto to:G[x])if(to!=fa&&!vis[to])dfs1(to,x,from);
cnt_col[c[x]]--;
}
对第二种情况,假设某种颜色 \(c\) 在 \(x\to y\) 的路径上已经出现过了,统计 \(y\) 的答案时,贡献直接是 \(sz[x]-sz[p]\),否则,应该对 \(p\) 以外的 \(x\) 子树进行统计,如果某个颜色在一个结点里第一次出现,则会产生其子树大小的贡献,记一个 \(path[c]\) 表示颜色 \(c\) 的贡献
void dfs2(int x,int fa,int def_val,bool tag){
cnt_col[c[x]]++;
if(cnt_col[c[x]]==1){
sum_col+=def_val;
sum_path-=path[c[x]];
}
ans[x]+=sum_path;
if(tag)ans[x]+=sum_col;
for(auto to:G[x])if(to!=fa&&!vis[to])
dfs2(to,x,def_val,tag);
if(cnt_col[c[x]]==1){
sum_col-=def_val;
sum_path+=path[c[x]];
}
cnt_col[c[x]]--;
}
因为需要扣除掉 \(p\) 子树内的 \(path\) 数组,直接给数组做差不方便,这部分答案可以考虑对 \(x\) 的孩子正反做两次dfs
void calc_path(int x,int fa){
cnt_col[c[x]]++;
Q[++tot]=c[x];
if(cnt_col[c[x]]==1){
path[c[x]]+=sz[x];
sum_path+=sz[x];
}
for(auto to:G[x])if(to!=fa&&!vis[to])calc_path(to,x);
cnt_col[c[x]]--;
}
//...
auto work=[&](bool tag){
clear();
sum_col=sum_path=0;
assert(cnt_col[c[x]]==0);
for(auto to:G[x])if(!vis[to]){
cnt_col[c[x]]++;
sum_col=sz[x]-sz[to];
dfs2(to,x,sz[x]-sz[to],tag);
calc_path(to,x);
sum_col=0;
cnt_col[c[x]]--;
}
};
work(0);
reverse(G[x].begin(),G[x].end());
work(1);
代码:
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define endl '\n'
#define fastio ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int N=1e5+5;
int n,c[N],mx_c;
bool vis[N];
vector<vector<int>> G;
int cnt_col[N],path[N];
int tot,Q[N];
ll sum_path,sum_col;
ll ans[N];
int rt,sz[N],mx_rt;
void get_rt(int x,int fa,int sum){
sz[x]=1;
int mx=0;
for(auto to:G[x])if(to!=fa&&!vis[to]){
get_rt(to,x,sum);
mx=max(mx,sz[to]);
sz[x]+=sz[to];
}
mx=max(mx,sum-sz[x]);
if(mx<mx_rt){
mx_rt=mx;
rt=x;
}
}
void dfs1(int x,int fa,int from){
cnt_col[c[x]]++;
if(cnt_col[c[x]]==1)ans[from]+=sz[x];
for(auto to:G[x])if(to!=fa&&!vis[to])dfs1(to,x,from);
cnt_col[c[x]]--;
}
void dfs2(int x,int fa,int def_val,bool tag){
cnt_col[c[x]]++;
if(cnt_col[c[x]]==1){
sum_col+=def_val;
sum_path-=path[c[x]];
}
ans[x]+=sum_path;
if(tag)ans[x]+=sum_col;
for(auto to:G[x])if(to!=fa&&!vis[to])
dfs2(to,x,def_val,tag);
if(cnt_col[c[x]]==1){
sum_col-=def_val;
sum_path+=path[c[x]];
}
cnt_col[c[x]]--;
}
void calc_path(int x,int fa){
cnt_col[c[x]]++;
Q[++tot]=c[x];
if(cnt_col[c[x]]==1){
path[c[x]]+=sz[x];
sum_path+=sz[x];
}
for(auto to:G[x])if(to!=fa&&!vis[to])calc_path(to,x);
cnt_col[c[x]]--;
}
void dfz(int x,int sum=n){
mx_rt=INF;
get_rt(x,-1,sum);
x=rt;
get_rt(x,-1,sum);
auto clear=[&](){
rep(i,1,tot)path[Q[i]]=0;
tot=0;
};
dfs1(x,-1,x);
auto work=[&](bool tag){
clear();
sum_col=sum_path=0;
assert(cnt_col[c[x]]==0);
for(auto to:G[x])if(!vis[to]){
cnt_col[c[x]]++;
sum_col=sz[x]-sz[to];
dfs2(to,x,sz[x]-sz[to],tag);
calc_path(to,x);
sum_col=0;
cnt_col[c[x]]--;
}
};
work(0);
reverse(G[x].begin(),G[x].end());
work(1);
vis[x]=true;
for(auto to:G[x])if(!vis[to])dfz(to,sz[to]);
}
int main(){
fastio;
cin>>n;
rep(i,1,n){
cin>>c[i];
mx_c=max(mx_c,c[i]);
}
G=vector<vector<int>>(n+1);
rep(i,1,n-1){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfz(1);
rep(i,1,n)cout<<ans[i]<<endl;
return 0;
}




