【图形学笔记】Lecture12-Path Tracing-路径追踪

Lecture12-Path Tracing-路径追踪

目录

• Lecture12-Path Tracing-路径追踪
  • Ray Casting 光线追踪
  • Ray-surface intersection 射线-表面判交
    • 光线和平面
    • 光线和三角形判交——Möller Trumbore算法
  • Ray Intersection With Sphere
  • Ray Intersection With Implicit Surface
  • Bounding Volumes——包围盒er
  • Uniform Spatial Partitions-均匀的空间划分
  • Non-Uniform Spatial Partitions:Spatial Hierarchies-不均匀的空间划分
    • KD-Tree
  • Object Partition&Bounding Volume Hierarchy（BVH）物体划分-层次包围盒

路径追踪=光追+蒙特卡洛方法

Ray Casting 光线追踪

• 通过追踪每个像素的光线，生成图片
• 通过光线能否到光源，来检查是否是阴影

Ray-surface intersection 射线-表面判交

光线和一个几何体的交点怎么算？对于封闭的几何体，只需要判断交点个数的奇偶性！

所以转换成与三角形网格的交点！（这样会有点慢，后面会有加速结构）

光线和平面

光线方程：

\[\vec r(t)=\vec o+t\vec d (0\leq t<\infty ) \]

平面方程（也写成向量的形式）：\((p-p')\cdot N=0\)（过 \(p'\) 点，以 \(N\) 为法向量）

联立代入，\((o+td-p')\cdot N=0\)，得到

\[t=\frac{(p'-o)\cdot N}{d\cdot N} \]

先 check 必要条件 \(0\leq t<\infty\)

光线和三角形判交——Möller Trumbore算法

先做完上一步，接着判断交点是否在三角形内，

平面是二维流形，对于三角形 \(P_0,P_1,P_2\)，可以把三角形内的点写成重心坐标的形式：

\[(1-b_1-b_2)P_0+b_1 P_1+b_2 P_2\equiv r(t)=\vec O+t\vec D \]

Möller Trumbore Algorithm：

整理一下：

\[\vec D t+(P_0-P_1)b_1+(P_0-P_2)b_2=P_0-O \]

这里其实就是Cramer法则（乘法对应的是混合积）：

整理系数得到线性方程（左边的行向量其实每个元素都是列向量，所以本质上是 \(3\times 3\) 的矩阵）：

\[\begin{bmatrix} \vec D&\vec P_{10}&\vec P_{20} \end{bmatrix}\cdot \begin{bmatrix} t\\b_1\\b_2 \end{bmatrix} =\vec P_0-\vec O \]

左边的行列式认为是混合积 \([\vec D,\vec P_{10},\vec P_{20}]=D\cdot (\vec P_{10}\times \vec P_{20})\) 根据Cramer法则：

\[\begin{bmatrix} t\\b_1\\b_2 \end{bmatrix} = \frac{1}{[\vec D,\vec P_{10},\vec P_{20}]} \begin{bmatrix} \vec {OP_0}\cdot (\vec P_{10}\times \vec P_{20})\\ \vec D\cdot (\vec{OP_0}\times \vec P_{20})\\ \vec D\cdot (\vec P_{10}\times \vec {OP_0}) \end{bmatrix} \]

和下面写的一大坨式子是一样的，现场推就好了（刚好每项差一个负号，最后全消掉了）：

然后检查 \(b_1,b_2,t\) 是否规范（\(\geq 0\)）即可。

Ray Intersection With Sphere

球：\((p-c)^2=R^2\)，代入\(r=o+td\)，得到\((o+td-c)^2=R^2\)，转化成

\[(d\cdot d) t^2+[2(o-c)\cdot d ]t+(o-c)\cdot (o-c)-R^2=0 \]

标准的二次方程。

Ray Intersection With Implicit Surface

光线和隐式曲面求交，即如果有\(f(\vec p)=0\)，就代入得到 \(f(\vec o +t\vec d)=0\)。

Bounding Volumes——包围盒er

• 可以预先处理每个物体的包围盒，判断交点之前先和包围盒进行一次判断。

• 进一步可以考虑怎么做某一维（\(x,y,z\) 方向）的判断（axis-aligned bounding box——坐标轴平行、轴对齐的包围盒），算出每一组面的 \(t_{\min},t_\max\) 的区间，再求个交集（\(t_{enter} = \max{t_{\min}}, t_{exit} = \min{t_{\max}}\)）

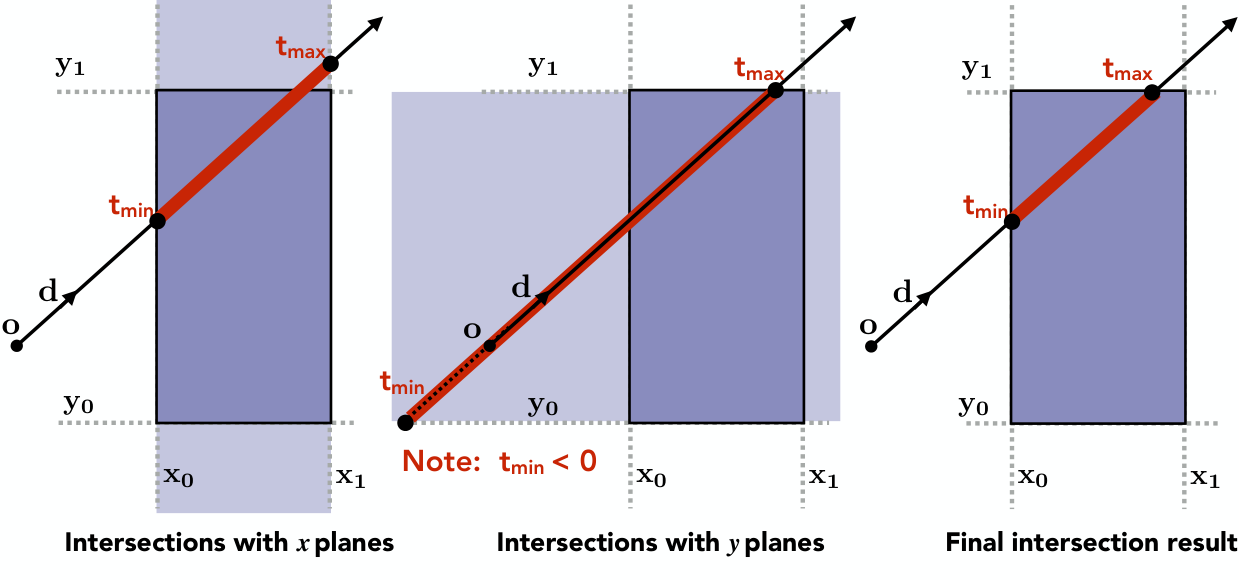
• 有交点当且仅当，\(t_{enter}< t_{exit}\) 且 \(t_{exit}\geq 0\).

• AABB是个啥？坐标平行的包围盒（Axis-Aligned Bounding Box）

• 平行的平面求交会更好算： \(o_x +t d_x=p_x\)，那么直接 \(t=\frac{p_x-o_x}{d_x}\)，只需要简单的减法和除法。

Uniform Spatial Partitions-均匀的空间划分

• 1、光追之前，先做出包围盒
• 2、对包围盒进行划分，创建网格。
• 3、光线跟每个小盒子判交，如果有交点，再和内部的图形判断。

很明显，划分出来的格子数量不能太大，也不能太小，通常个数=某个常数 $\times $ 物体数量。

当然也有一些问题，比如它给了个“teapot in a stadium“，就是说一个很大的空间里，放了一个茶杯，那这种空间划分就很鸡肋。

Non-Uniform Spatial Partitions:Spatial Hierarchies-不均匀的空间划分

Oct-Tree 八叉树，KD-Tree，BSP-Tree空间划分树

KD-Tree

没什么好讲

按顺序遍历，光线求交。

Object Partition&Bounding Volume Hierarchy（BVH）物体划分-层次包围盒

KD树一个物体可能出现在多个节点里，而且对于一个固定的包围盒，判断一些图形是否在包围盒里，可能并不是很容易（比如三角形和立方体），所以就有了BVH的需要。

当然BVH也有个不好的地方，就是两个结点的包围盒可能是有交的。

如何划分空间？

• 比如 \(x,y,z\) 交替比较。
• 按照某一位排序，根据中位数划分，让左右两边的图形个数尽可能接近。
• 不管是KD树还是BVH，都是希望最小化期望的查询次数（毕竟用在光线追踪里面，光线是随机取的）