【图形学笔记】Lectre11-The Rendering Equation-渲染方程

Lectre11-The Rendering Equation-渲染方程

目录

• Lectre11-The Rendering Equation-渲染方程
  • Models of Scattering 散射模型
  • 表面散射——BRDF（双向反射分布函数）
    • 一个点上的反射
    • 镜面反射
    • Transmission 传播（似乎是折射)
    • Fresnel reflection菲涅尔反射
    • Subsurface scattering 表面下的散射

回顾一下，irradiance（E）跟辐射度/辐照度radiance（L）有如下关系：

\[E=\int_{H^2}L(\omega)\cos\theta d\omega \]

这里 \(L(\omega)\) 表示沿着 \(\omega\) 方向的

渲染器的核心，是在给定一个方向 \(\omega_0\) 以及点 \(p\) 的情况下，估算亮度。

本节最重要的渲染方程（Kajiya）：

函数 \(f_r (p,\omega _i\to \omega _o)\) 是一个用来衡量反射光和入射光之间关系的散射函数（scattering function）。

Models of Scattering 散射模型

如何给散射光建模？这情况可非常多：

• 从表面直接反弹（反射）
• 透过表面传播
• 在物体里面反射
• 被吸收，或者等待一段时间被重新发射（？？）

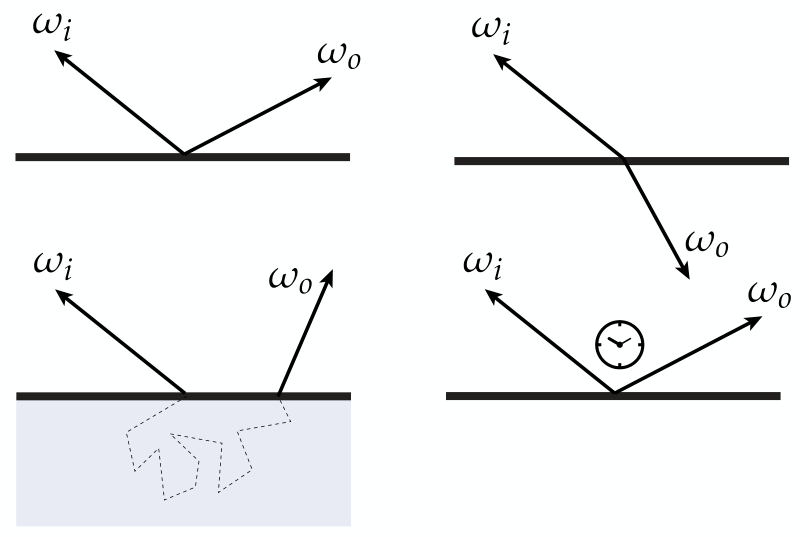
我们去谈，一个粒子从入射方向散射到另一个方向的概率！

• 漫反射（Diffuse reflection）：所有方向的出射光是一样的。
• 理想镜面反射（Ideal specular reflection）：出射光相当于沿着法向量“翻转”。
• 塑料材质（Plastic）：翻转并且模糊（blurred）。

表面散射——BRDF（双向反射分布函数）

BRDF的全称是：Bidirectional reflectance distribution function 双向反射分布函数

• 编码了光线在表面反射的行为。

• 对于给定的入射方向 \(\omega_i\)，有多少光线从给定的方向 \(\omega_o\) 散射出去？

• 用一个分布还是 \(f_r(\omega_i\to\omega_o)\) 来描述！

• 此时自然有 \(f_r\geq 0\) ，并且因为能量守恒，所以

  \[\int_{H^2} f_r(\omega_i\to\omega_o) \cos\theta d\omega_i\leq 1 \]

• 以及根据一个叫Helmholtz互反律（reciprocity）的东西，有\(f_r(\omega_i\to \omega_o)=f_r(\omega_o\to \omega_i)\)。

• \(f_r\) 如何刻画？

一个点上的反射

• 根据渲染方程， \(f_r\) 应当是 \(L_r\) 与 \(E_i\) 的比值！
• 设 \(\omega_i\) 表示入射方向， \(\omega_r\) 表示反射方向，那么

\[f_r(\omega_i\to \omega_r)\equiv \frac{dL_r(d\omega_r)}{d E_i (\omega _i)}=\frac{dL_r(d\omega_r)}{L_i(\omega_i) \cos\theta_i d\omega_i} \]

• 特别地，如果 \(f_r\) 都一样，那么根据渲染方程 \(L_o=f_r \int_{H^2} L_i(\omega_i) \cos\theta_i d\omega_i=f_r\cdot E\)。
• 这里似乎有个物理学背景，\(f_r=\rho/\pi\)，这里\(\rho \in[0,1]\) 叫做albedo反射率。

镜面反射

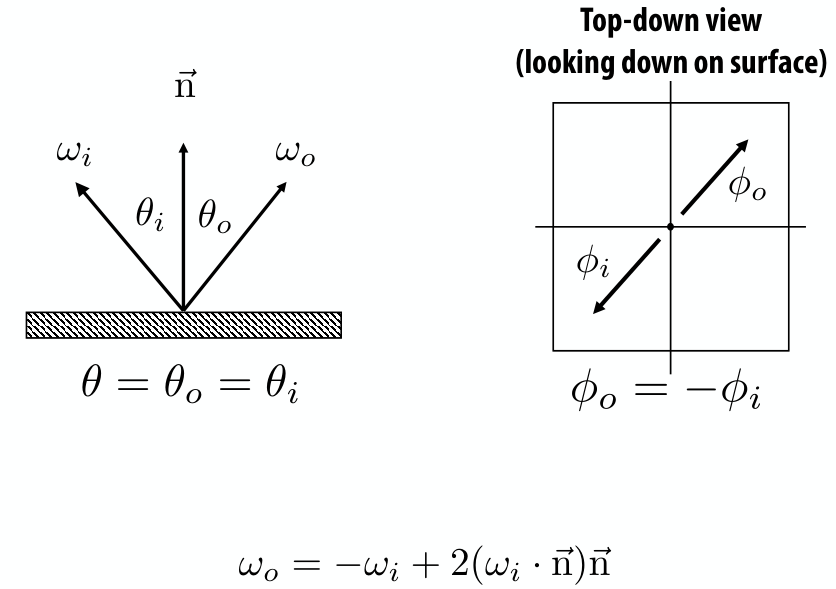
非常直观，\(-\omega_i\) 后面需要的是 \(\omega_i\) 在 \(\vec n\) 上的投影长度：

\[\omega_o=-\omega_i+ 2\vec n(\vec n\cdot \omega_i) \]

那么对于镜面反射，入射光和反射光应该是对称的，所以只有在一些特定的地方有取值。

• 狄拉克 \(\delta\) 函数（Dirac delta）：并不懂它这里的狄拉克函数怎么定义的，因为标准定义似乎并不是一个严格的函数，而是这样一个函数：
  • \(\delta(x)\) 仅在 \(x=0\) 处为非零，其他地方取值为0，但是在\(\R\) 上的积分又是1，很明显这样的函数是不存在的。
  • 但实际的物理应用里，会用一些近似的函数来逼近。

这里就用到了狄拉克函数:

\[f_r(\omega_i\to \omega_o)=f_r(\theta_i,\phi_i,\theta_o,\phi_o)\equiv \frac{\delta(\cos\theta_i-\cos\theta_o)\delta(\phi_i-\phi_o\pm \pi)}{\cos\theta_i} \]

这里\(\phi,\theta\) 是两个方向的夹角（看上一张图），而\(/\cos \theta _i\) 则对应着Lambert的余弦定律。

• 所以在实践中，不会去通过随机采样找反射方向，而是直接计算。

Transmission 传播（似乎是折射)

作为直接在表面反射的补充，光也可能穿过物体传播

• 斯涅耳定律（Snell's Law）：\(\eta_i \sin \theta_i=\eta_t \sin\theta t\)，经过一顿计算，可以得到

  • \[\cos \theta_t =\sqrt{1-(\frac{\eta_i}{\eta_t}^2)(1-\cos^2\theta_i)} \]

  • 可以看出来，如果角度太大，可能直接没有折射光了（这时候对应的反射就是全反射）

Fresnel reflection菲涅尔反射

似乎是模拟菲涅尔效应。

Subsurface scattering 表面下的散射

需要去推广散射模型——BSSRDF（什么玩意？）