【图形学笔记】Lecture10-Radiometry-辐射度量学

Lecture10-Radiometry-辐射度量学

目录

• Lecture10-Radiometry-辐射度量学
  • 一些概念
    • Solid angles 立体角
    • Differential solid angle 立体角的导数
    • 辐射度量学
      • Radiant flux (power)
      • Radiant intensity
      • Irradiance
      • Radiance

动机：前面的反射模型太粗糙啦…而且很多是经验公式。

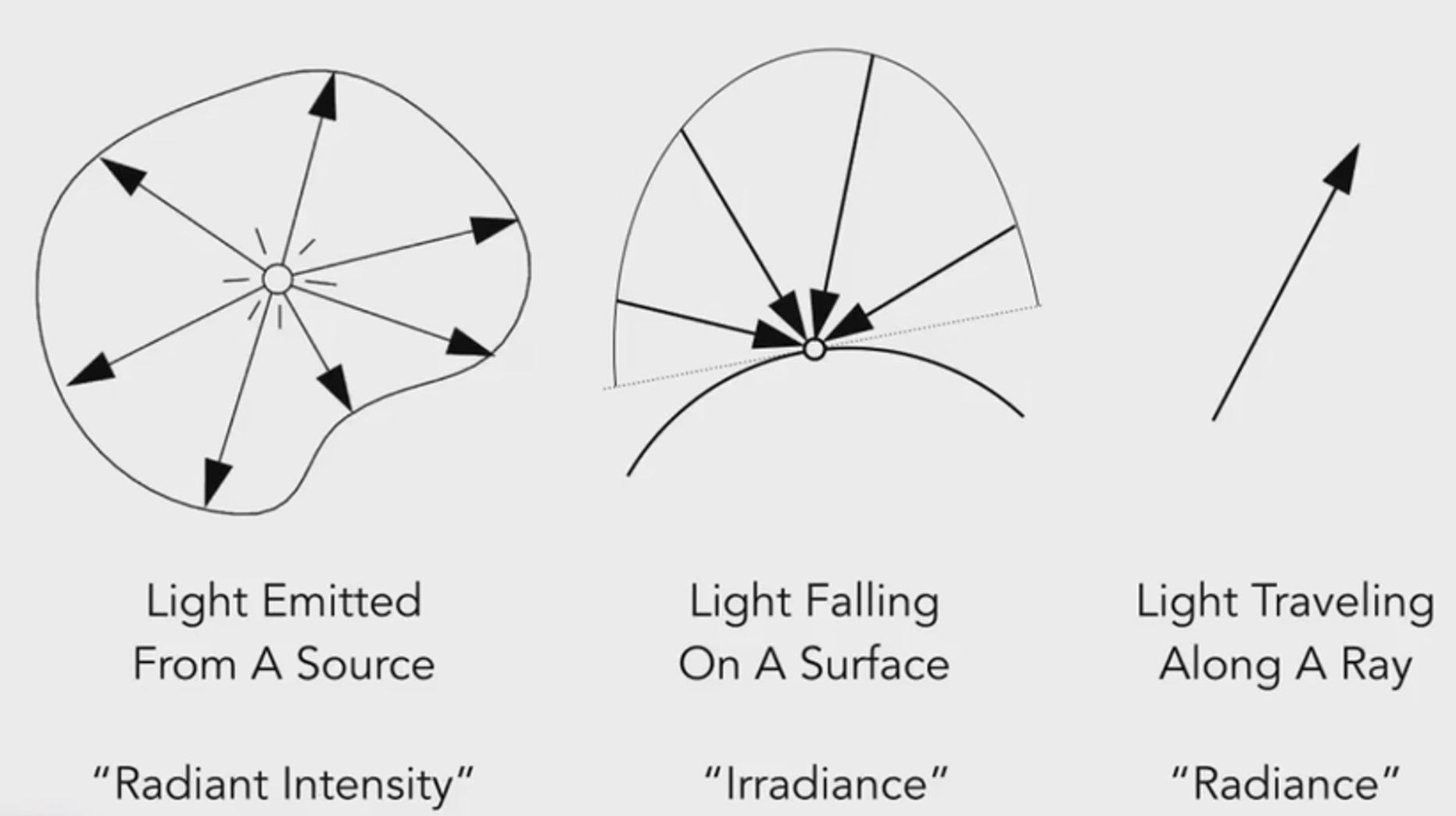
几个关键概念：Radiant flux，intensity，irradiance，radiance

光线追踪vs.光栅化

• [局部]光栅化器一次处理一个基本单元，很难确定诸如“A在B的阴影下”之类的事情。
• [全局]射线追踪器处理一条射线，射线知道所有它相交的地方，很容易谈论阴影和其他“全局”照明效果。

一些概念

Solid angles 立体角

立体角（类比于角度=弧长/半径）：

\[\omega =\frac{A}{r^2} \]

Differential solid angle 立体角的导数

平面角（球坐标系）：

\[dA=r^2 \sin \theta d\theta d\phi \]

那么微分立体角（differential solid angle）：

\[d\omega=\frac{dA}{r^2}=\sin\theta d\theta d\phi \]

绕一圈也很明显有\(\Omega =\int_{S^2} \sin\theta d\theta d\phi=4\pi=\frac{4\pi r^2}{r^2}\)。

辐射度量学

Radiant energy is "total # of hits"——辐射能量=所有打到场景的光子个数，用的不多。

Radiant flux (power)

• Radiant flux/power 辐射通量=单位时间内的辐射能量，类似于“光照强度”

Radiant intensity

• 单位立体角的辐射通量

\[I(\omega)=\frac{d\Phi}{d\omega} \]

那么 \(\Phi=\int I d\omega\)，考虑球面，就有 \(I=\Phi/(4\pi)\)。

Irradiance

• 辐照度（irradiance）= 单位面积的辐射通量（radiant flux），辐射度也叫辐射通量的密度（Radiant Flux Density）

  \[E(\vec x)=\frac{d \Phi(\vec x)}{d A} \]

  注意这里的 \(A\) 是有向的，即单位面积和辐射要是垂直的，如果不是垂直的话，则需要算上 Lambert's cosine law，转化成投影的面积。

• Projected area-Lambert’s Law

  • 考虑一条辐射通量 \(\Phi\) 的光线，打入了一个面积为 \(A'\) 的面，面的法向量和光线有个夹角 \(\theta\) ，那么实际上投影的面的面积只有 \(A=A'\cos \theta\) ，辐照度

\[E=\frac{\Phi}{A'}=\frac{\Phi\cos \theta}{A} \]

• 进一步，着色的时候需要乘上一个单位法向量 \(n\) 和（单位）光源方向 \(L\) 的点积。

double surfaceColor( Vec3 N, Vec3 L ){
	return max( 0., dot( N, L ));
}

Radiance

\[L(p,\omega)=\frac{dI}{dA}=\frac{dE}{d\omega}=\frac{d^2 \Phi}{dA d\omega (\cos\theta)} \]

表示单位时间内，单位面积上，单位立体角向指定长度辐射的能量。

那么Irradiance 的微元\(dE=L(p,\omega)\cos \theta d\omega\)，所以就得到了本节最重要的公式：

\[E(p,\omega)=\int_{H^2} L_i(p,\omega)\cos\theta d\omega \]

下标 \(i\) 表示的应该是“入射”的意思。

对于最朴素的情况，即\(L_i\) 的取值都一样（四面八方辐射进来的Radiance都一样），那么会得到 \(E=\pi L\).

特别地，课件上还提到了一种情况，光源的Radiance都是L，然后投到了球面上的一个区域 \(\Omega\) ，那么

\[E(p)=\int_{H^2} L\cos \theta d\omega=L\int _\Omega \cos\theta d\omega\equiv L\cdot \Omega^{\perp} \]