【图形学笔记】Lecture07-Introduction to Geometry几何
Lecture07-Introduction to Geometry几何
显式的(explicit)几何表示方法:点云(point cloud)、多边形网格(polygon mesh)、细分(subdivision)…
隐式的(implicit)表示方法:等值面(level set)、代数曲面(algebraic surface)…
Implicit Surface 隐式的曲面
形如
- 找到哪些点在面上通常是困难的,但是判断一个点在哪里是比较简单的!
CSG-Constructive Solid Geometry(Implicit)构造刚体几何图形
集合运算跟逻辑运算是对应的,所以就可以用集合的交并补差这些运算,来处理图形。
Blending Distance Functions 融合距离函数
对于几何,不去描述表面,而是描述点到表面的最近距离。
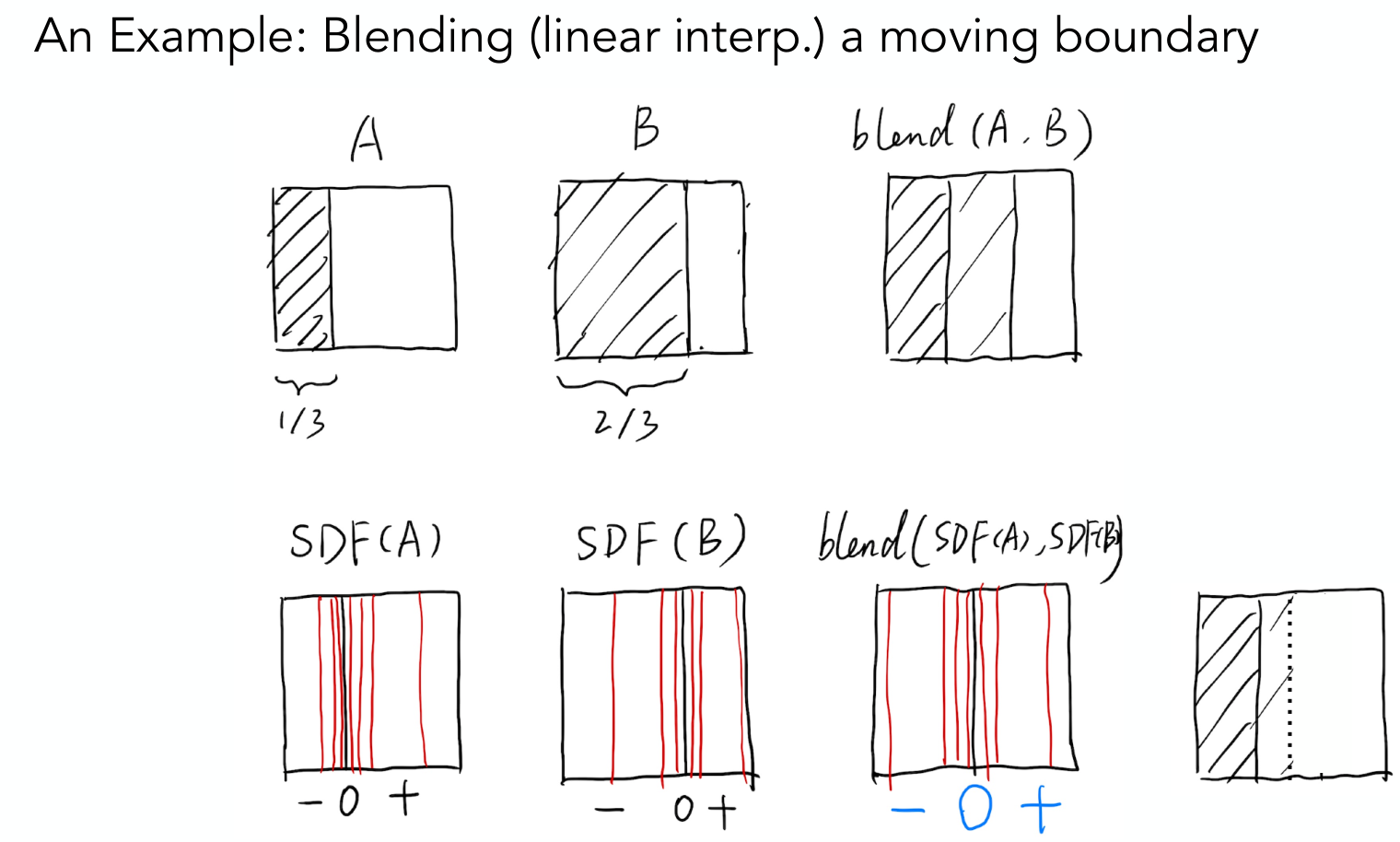
假设想要求出上图中,
Level Set Method 水平集方法
有了混合的距离函数,如何再恢复表面呢?把SDF=0的地方找出来,如果函数是隐式的,那就类似光栅化那样采样,然后用插值的方法求出等值面。
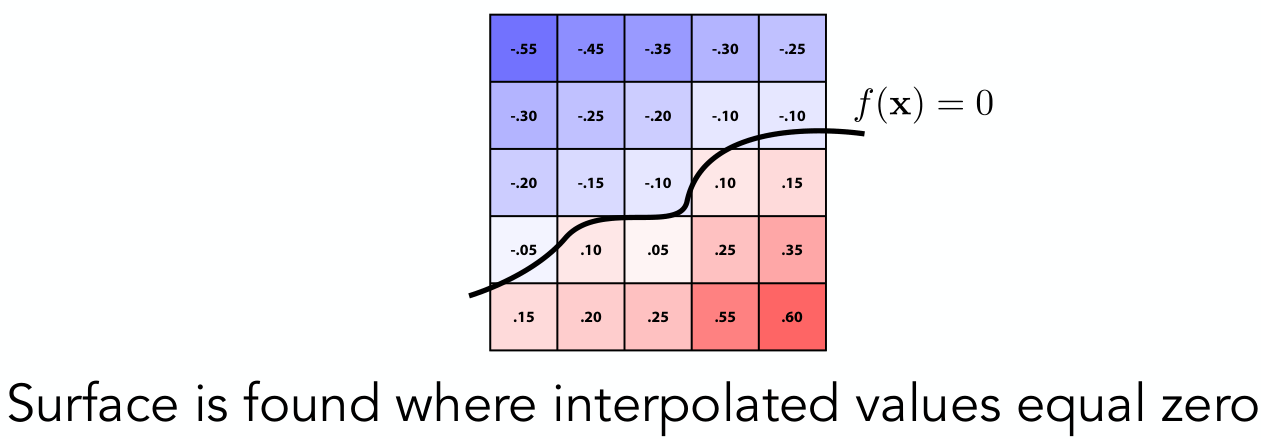
Fractal 分形
复杂的情况~在渲染的时候可能会引起强烈的走样。
Explicit Representation 显式的表示
- 找到哪些点在面上会变简单(比如参数方程的表示,只要跑遍所有参数的取值,也必须跑遍),但是判断一个点在哪里变难了!
所有点直接给出/通过参数坐标给出,比如课件上给了个
接着就开始说极坐标表示点,上面提到的轮胎面还可以表示成
(补充)
Point Cloud 点云
用一系列的点
Polygon Mesh 多边形网格
-
存储点和多边形
-
很容易做处理、模拟、自适应采样
-
更加复杂的数据结构
-
在图形学里更经常用的表示方法
Splines 样条曲线
样条(spline):一条连续的曲线,经过一系列给定的控制点,并且满足一定的连续性。
Cubic Hermite Interpolation 三次Hermite插值
- Nearest Neighbor Interpolation:
- Linear Interpolation:线性插值,函数连续,导数不连续。
- Cubic Hermite Interpolation(三次厄尔米特插值):可以让导数连续!
Power Basis 幂基
幂基(power basis):
然后对于一个
Useful Properties of a Basis 基的一些有用性质
这部分在课件里放在贝塞尔曲线,但我感觉提上来比较好。
Convex Hull property 凸包性质
- 凸包性质指的是:所有曲线上的点都落在控制点的凸包内。
- 贝塞尔曲线具有这种性质。
- 基满足凸包性质,若:
- 基函数的和为1,即:
- 基函数非负:
- 基函数的和为1,即:
Invariance 不变性
这里特指:对曲线做某个变换=对控制点做变换,再绘制曲线
即:
- 贝塞尔曲线对仿射变换具有不变性,但对透视变换不具有不变性,即:
这条性质感觉得通过Bernstein多项式来写?(不知道有没有更直接的方法,直接乘矩阵肯定是不能交换的)
Local Support 局部支撑
改变一个控制点,不会改变整个曲线。
Some Differential Geometry 一些微分几何
一条曲线在某方向的切线可以写成
当然也有一些退化情况(比如
好了说了这么多,其实不知道他这页PPT放了有什么意义…
Specifying a Curve 特定曲线
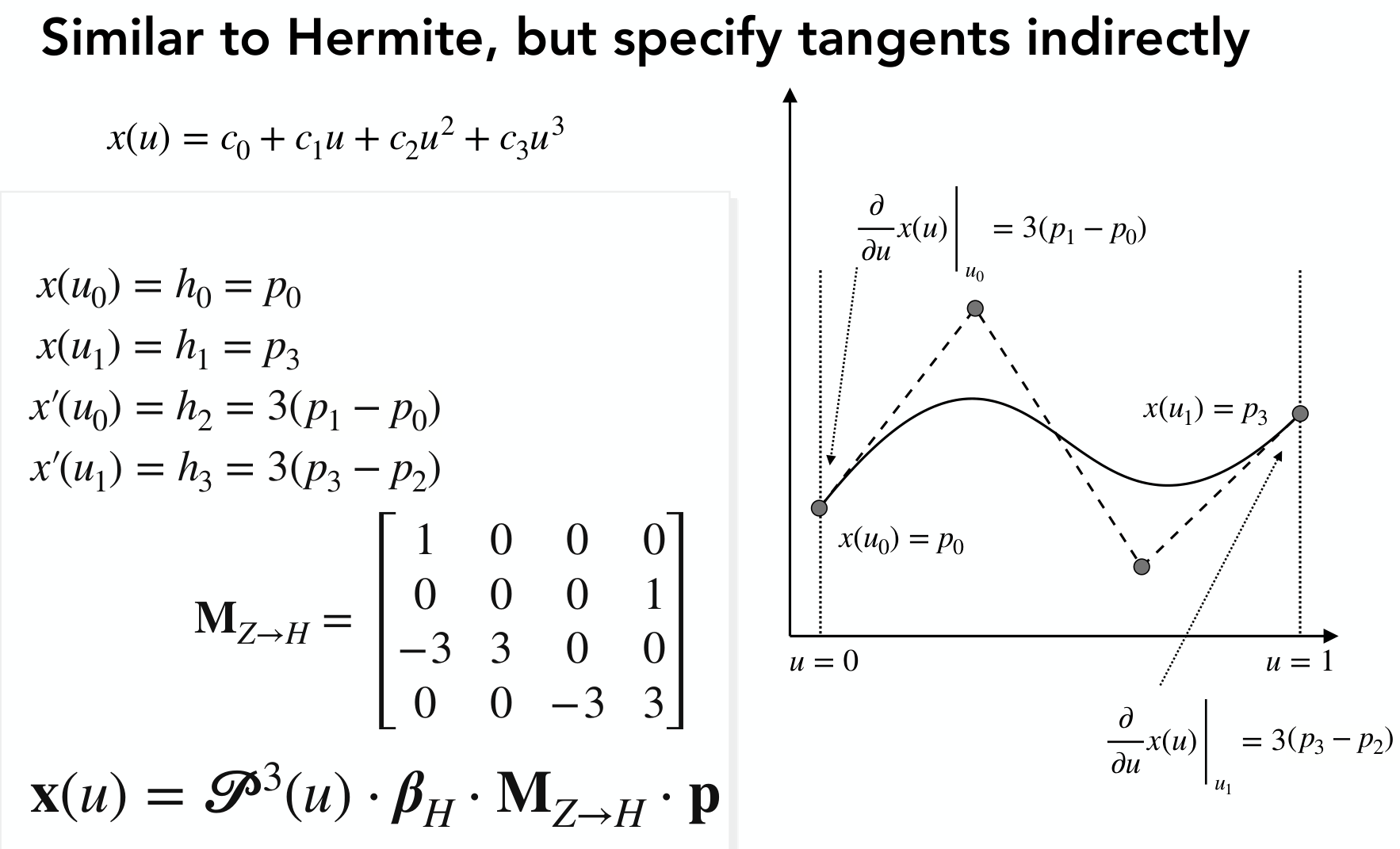
给了一些希望有的限制,如何确定三次幂基的系数(这句话有点绕,其实就是确定一个三次曲线的系数)?
即:已知
好,首先:
不妨假设
写成矩阵,即:
我们把左边的列向量
注:Hermite基矩阵:
此时任意一点
如果控制点发生变化,其实幂基、Hermite基矩阵都不会改变,所以
综上所述,三次Hermite插值是这样一个过程:输入端点函数值、导数值,输出一个三次多项式,最终的结果就是Hermite基的带权和(其实就是矩阵乘完的结果啦)!
得到的Hermite基函数(的各个分量):
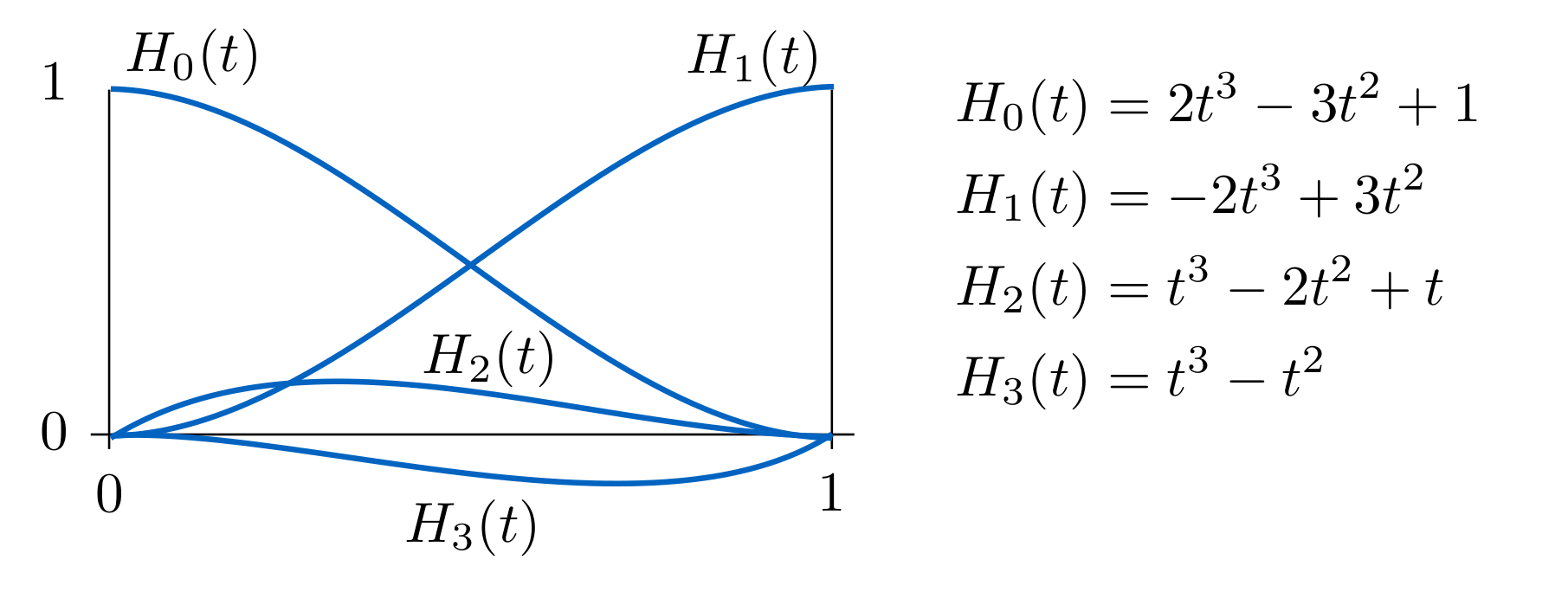
Q:为什么不用更高阶的多项式?
A:1、高阶多项式更不稳定,容易摆动。2、希望编辑后,能保持一些局部的性质(局部不要变化太大)3、开销大。
Catmull-Rom 插值
输入一些点,输出C1连续的经过所有插值点的样条。
导数的确定方式:
是一种逐段的(piecewise)三次曲线,并且非常容易推广到对
确定了导数之后,剩下的内容其实和三次Hermite插值一样,上面的
中间两个矩阵的结果就叫
Bézier Curve 贝塞尔曲线
Evaluating Bézier Curves——Matrix Formula 矩阵表示
和之前的Hermite、Catmull-Rom相比,还是改了个切线的定义方式——所有的控制点都是空间中的点,没有切线,而是让左右两个端点处的切线,恰好是连线(虽然这里有个系数
然后也类似有一个矩阵
可以得到一个基函数的图像:
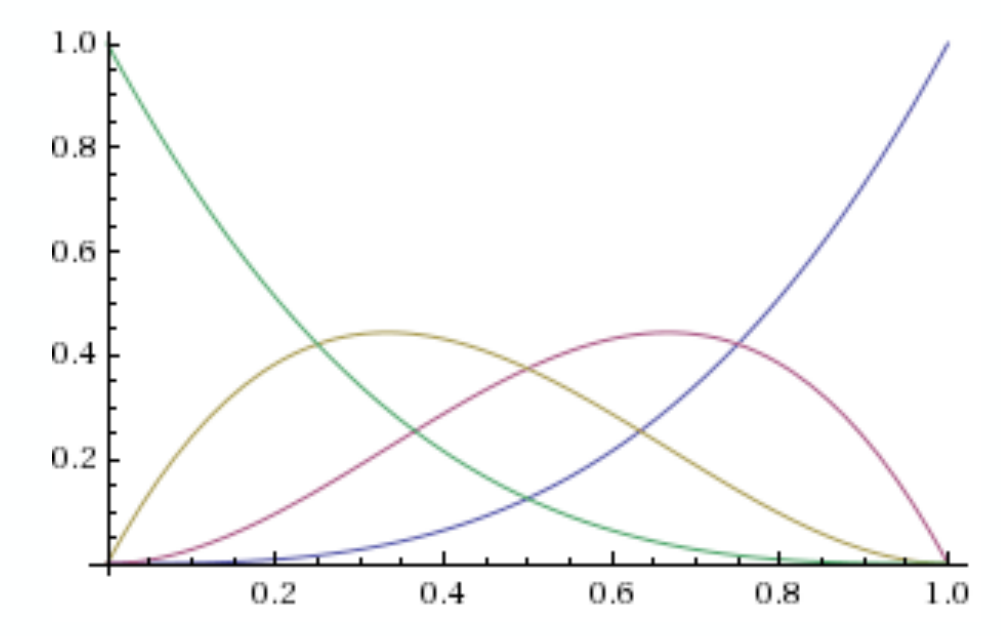
Evaluating Bézier Curves——De Casteljau Algorithm
对于
Evaluating Bézier Curves——Bernstein Polynomial
贝塞尔曲线迭代
注意,
那么特别地,对于一个三次贝塞尔曲线,有:
系数 3 就在这里。
Properties of Bézier Curve 贝塞尔曲线的性质
- 插值端点:
- 切线端点:对于3次贝塞尔曲线(4个控制点),
- 仿射变换不变性:贝塞尔曲线做仿射变换=控制点做仿射变换,再绘制贝塞尔曲线。
- 凸包性质:绘制的图形一定在控制点构成的凸包内部。
- 良好的表现:局部控制(加入点时?)
Piecewise Bézier Curves 逐段贝塞尔曲线
普通的贝塞尔曲线有个不好的地方,次数一旦高了,就不好通过控制点控制!
所以就有了逐段贝塞尔曲线——把很多段低阶的贝塞尔曲线,按顺序拼接起来,应用非常广泛(比如Photoshop的钢笔工具,绘制路径,很多矢量图的存储方式也是用这种曲线)
然后就是注意一点差异,我们平常在Photoshop里的钢笔工具是比较规范的,实际上的逐段贝塞尔曲线,可能不是C1连续的:
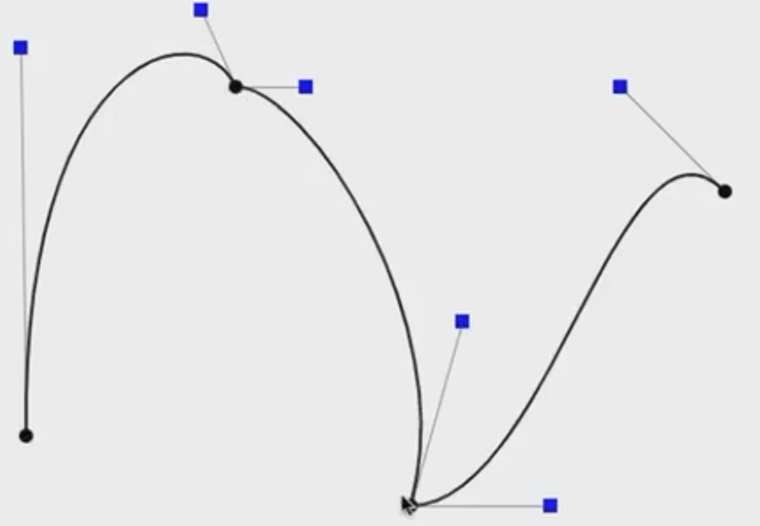
想象下面两段3阶贝塞尔曲线拼接起来,
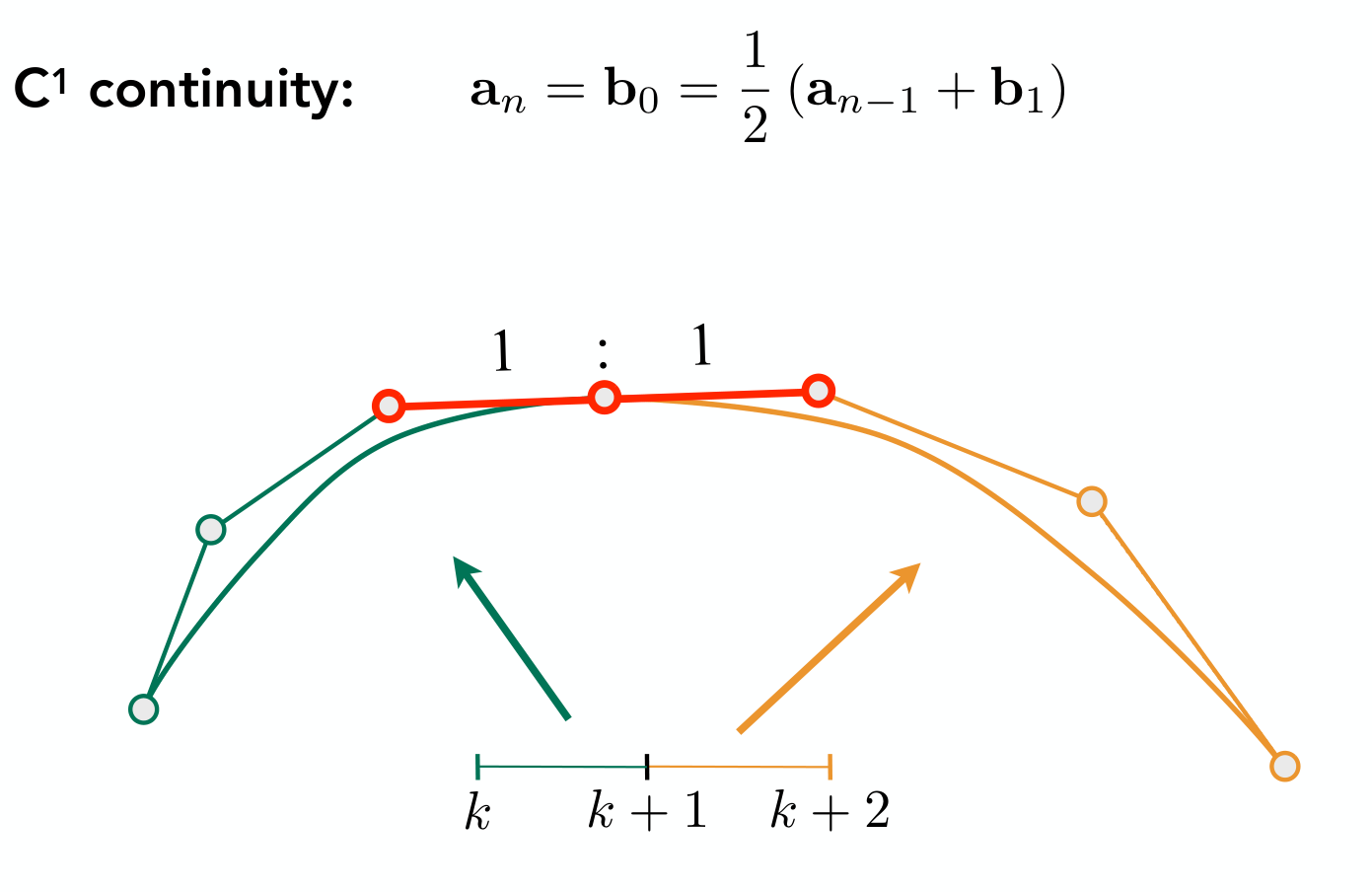
Bézier Surfaces 贝塞尔曲面
通常是用
Method 1: Separable 1D de Casteljau Algorithm
方法1就是说,对于
Method 2: Algebraic Evaluation
方法2是代数方法,推广一下上面的Bernstein多项式的写法:
课件上管这玩意叫张量积(Tensor product),给我吓得不轻。
Method 3: Linear Algebra
其实三个方法思路都一样,都是对两个方向进行线性插值。
方法3还是考虑前的形式,
最后写出来:
Method 4: Bézier Subdivision
方法4和之前的都不太一样!切入点应该是考虑贝塞尔曲线的凸包性质,进一步考虑找到一个合适的中点——即参数
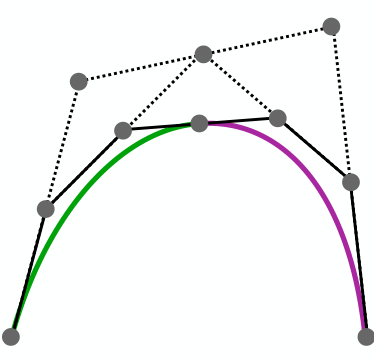
这里
类似地,另一半也可以写成




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律