【图形学笔记】Lecture05-Shading 着色

Lecture05-Shading 着色

目录

• Lecture05-Shading 着色
  • Diffuse Reflection 漫反射
  • Specular Shading (Blinn-Phong） 镜面反射
  • Ambient Shading 环境光
  • Shading Triangle Meshes 三角形网格着色
    • Per-Vertex Normal Vectors
    • Per-Pixel Normal Vectors

Shading：Definition

• The process of applying a material to an object.把材质应用于物体的过程

Blinn-Phong 反射模型：

镜面高光（Specular highlights）、漫反射（Diffuse reflection）、环境光（Ambient lighting）

Diffuse Reflection 漫反射

光线均匀地散射到所有方向，从所有方向看到的颜色是相同的，但是明暗可能不同。

Lambert 余弦定律：

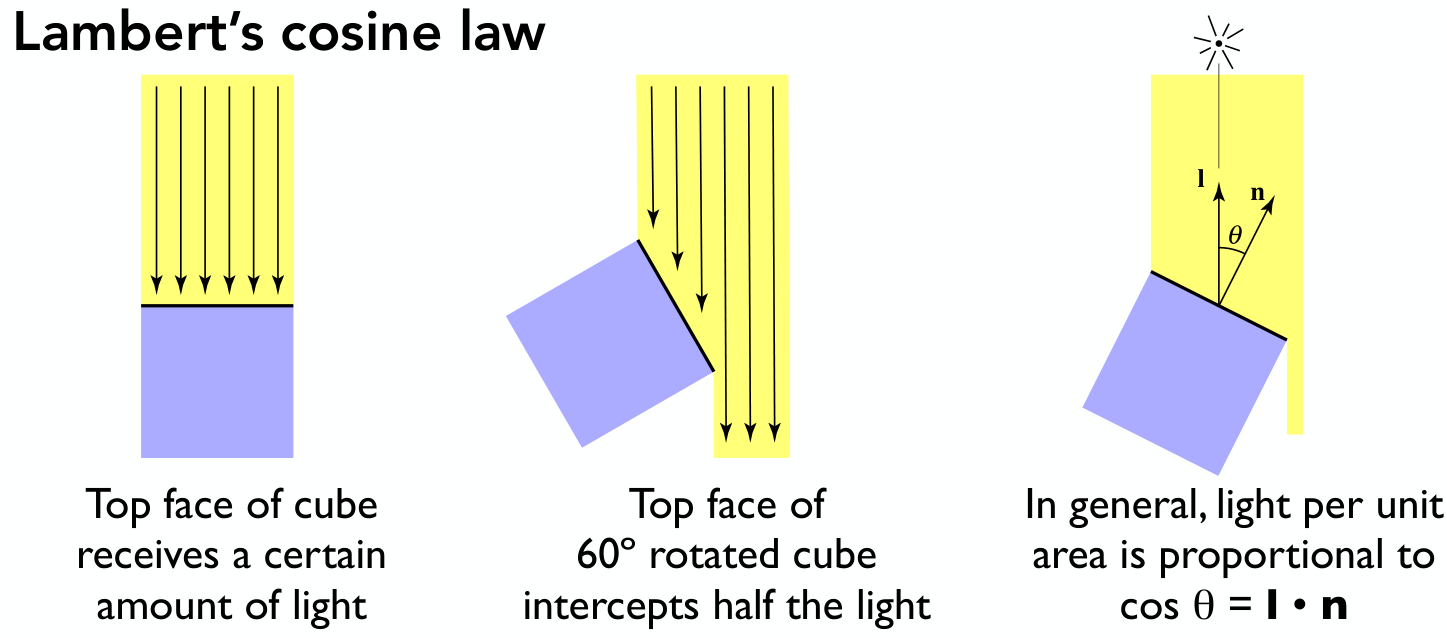
能量衰弱，平方反比定律——假设在距离光照中心距离为单位长度的位置，光照强度是 \(I\) ，则距离为 \(r\) 的地方的光照强度（intensity）应该是 \(I/r^2\) （能量守恒）。

漫反射光强

\[L_d=k_d\cdot \frac{I}{r^2} \max(0,\bf{n\cdot l}) \]

其中 \(k_d\) 是漫反射（diffuse）系数，如果是\(1\) 意味着完全反射了能量， \(0\) 则对应完全吸收了（实际上可能对RGB分别设置系数）。

\(I\) 是源点的光强，\(\bf{n}\) 是表面的法向量，\(\bf{l}\) 是反射的向量（这里假设都是单位向量，因此点乘其实就是算余弦）。

Q：这个漫反射看着和 \(\bf{v}\) 没什么关系？

A：确实，漫反射向四面八方反射的效果应该是一样的才对。

Specular Shading (Blinn-Phong） 镜面反射

接近镜面反射，通常意味着：反射方向和观察的方向很接近，进一步，意味着 \(\vec{I}+\vec v\) 和法线很接近！

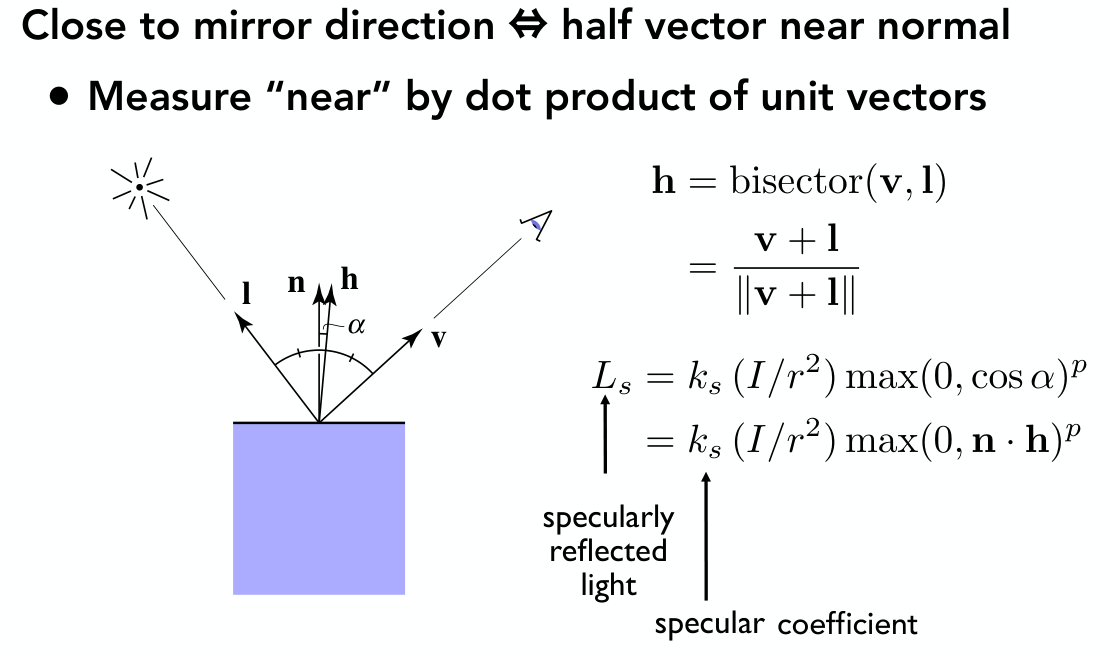
半程向量\(\bf{h}=bisector(v,l)=\frac{v+l}{|v+l|}\) （因为都是单位化的），镜面反射光：

\[L_s= k_s \frac{I}{r^2} \max(0,\bf{n\cdot h})^p \]

\(k_s\) 代表镜面反射（Spectacular）系数，\(p\) 通常会取到比较大的值（100到200）

Ambient Shading 环境光

大胆假设：任何点接收到的环境光是相同的！（？）那么很明显，环境光和位置、观测方向没什么关系，应该是一个常数！

最终

\[L=L_a+L_s+L_d=k_a I_a+ k_d \frac{I}{r^2}\max (0,\vec n\cdot \vec l)+k_s \frac{I}{r^2} \max(0,\vec n \cdot \vec h)^p \]

Shading Triangle Meshes 三角形网格着色

• 给每个三角形着色（flat shading：平面着色）——对光滑的表面效果不太好
• 给每个顶点着色（Gouraud shading ）——颜色插值，每个顶点定义一个法向量
• 给每个像素着色（Phong shading）——通过每个三角形，插值出法向量，对每个像素按照完整的着色模型计算。

Per-Vertex Normal Vectors

顶点的法向量怎么定义？和顶点相邻的面的法向量求平均：

必要时，加权（面积）平均效果会更好。

Per-Pixel Normal Vectors

重心插值，在下一个Lecture讲。