SDU Open 2023-H、几何、积分、单调栈维护上凸壳

SDU Open 2023-H、几何、积分、单调栈维护上凸壳

题目：https://codeforces.com/gym/104324/problem/H

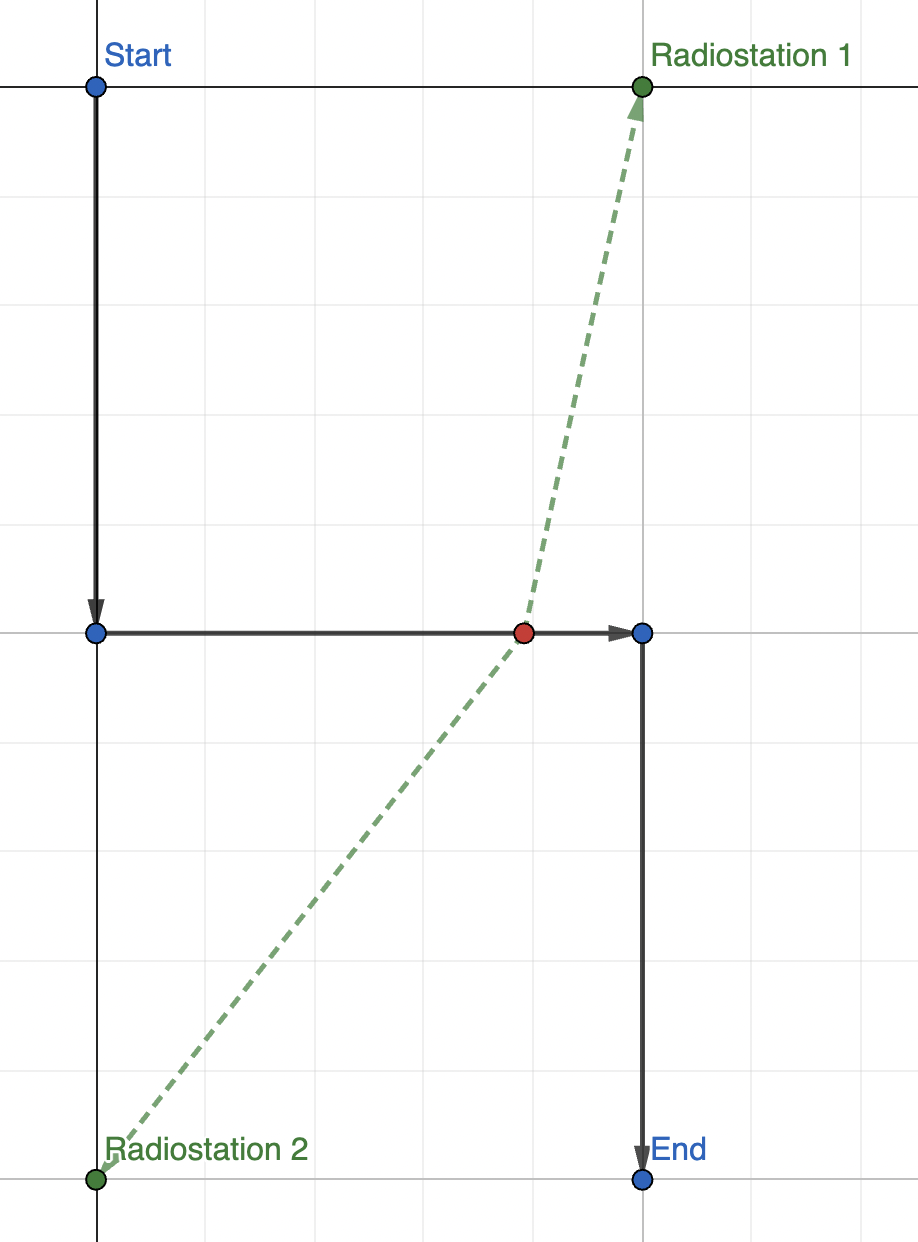
题意：有 \(n\) 个信号基站，你在边玩手机边走路，手机会自动连接到最近的基站。单位时间花费的流量是到基站距离的平方，现在从起点沿着直线走到终点，并且走的都是横平竖直的直线，单位时间移动单位距离，问最后花费了多少流量。

$ 1\leq n\leq 2000,1\leq m\leq 500$.

---

题解：

首先对走的每个折线段（至多 \(500\) 个）单独考虑流量花费，更进一步只考虑横着走的（把 \((x,y)\) 交换就可以做另一半），如此一来，考虑从某个 \((a_t ,b)\to (a_{t+1},b)\) 的折线段，这个过程中，只有 \(a\) 在动，中间每个基站 \((x_i,y_i)\) 到我的距离平方是：

\[(x_i-a)^2+(y_i-b)^2=a^2-2ax_i+x_i^2 +(y_i-b)^2=-2ax_i+\big(x_i^2+a^2+(y_i-b)^2\big) \]

后半部分除了 \(a^2\) 都是常数，而当我们对多个基站进行比较的时候，所有的 \(a^2\) 都是一样的，因此也可以直接忽略，这样一来在路径上每个位置，就只关心 \(-2ax_i +(x_i^2 +(y_i-b)^2)\) 最小的是哪个基站。这是关于 \(a\) 的一次函数！（记住，我们的自变量是 \(a\) ）

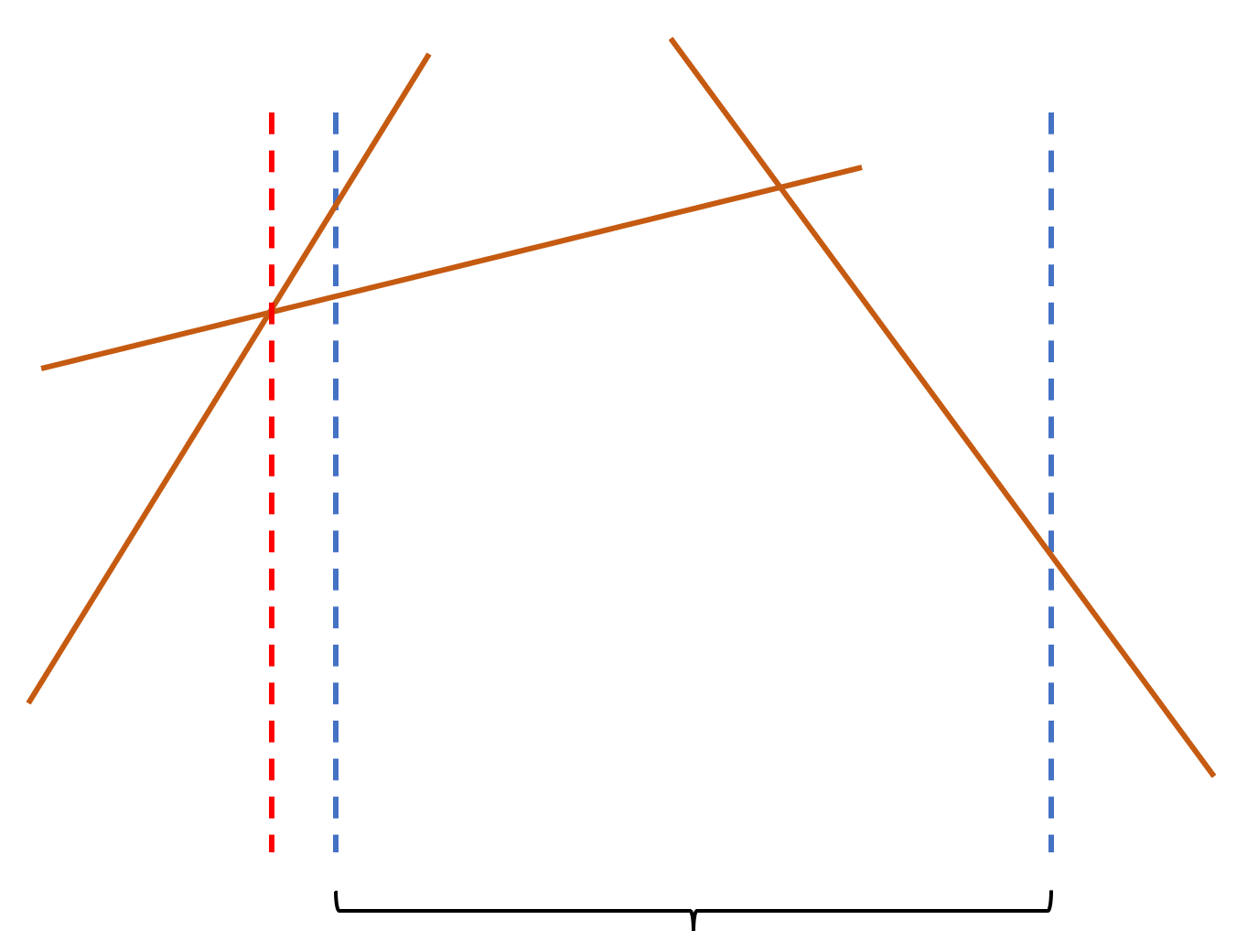
因此把 \(-2x_i\) 看成斜率，$x_i^2 +(y_i-b)^2 $ 看成截距，就转化成单调栈维护上凸壳了。

实现的时候需要注意，如果两条直线的交点在区间外（即 \([\min(a_t,a_{t+1}),\max(a_t,a_{t+1})]\) 的话需要弹掉），以及可以把第 \(0\) 条直线设成左端点，这样一来第一条直线其交点横坐标就直接是左端点。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define fastio ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=2005;
const int M=505;
struct point{int x,y;}pt[N];
struct line{
	ll a,b,idx;
	line(ll a=0,ll b=0,int idx=0):a(a),b(b),idx(idx){}
	bool operator <(line rhs){return a>rhs.a;}
	ld calc(ld x){return a*x+b;}
}l[N],stk[N];

ld get(line L1,line L2){return ((ld)(L2.b-L1.b))/(L1.a-L2.a);}
int n,m,sz;
ld ans,x[N];
int a[M],b[M];

ld f(ld x,ll b,ll c){return x*x*x/3+x*x*b/2+x*c;}
ld INT(ld l,ld r,ll b,ll c){return f(r,b,c)-f(l,b,c);}
void work(){
	rep(tc,1,m-1)if(b[tc]==b[tc+1]){
		sz=0;
		int mi=min(a[tc],a[tc+1]),mx=max(a[tc],a[tc+1]);
		rep(i,1,n){
			ll A=-2*pt[i].x,B=pt[i].x*pt[i].x+(pt[i].y-b[tc])*(pt[i].y-b[tc]);//1e8+1e8
			l[i]=line(A,B,i);
		}
		sort(l+1,l+n+1);

		x[0]=mi;
		rep(i,1,n){//单调栈维护上凸壳,x[i]表示第i条直线和第i+1条直线的交点的横坐标,特别地[min,max]两端要放两条垂直的直线卡住
			while(sz&&stk[sz].calc(x[sz-1])>=l[i].calc(x[sz-1]))sz--;
			stk[++sz]=l[i];
			if(sz>=2){
				x[sz-1]=get(stk[sz],stk[sz-1]);
				if(x[sz-1]<mi||x[sz-1]>mx)sz--;
			}
		}
		x[sz]=mx;
		rep(i,1,sz){//计算积分
			int idx=stk[i].idx;
			ll B=-2*pt[idx].x;
			ll C=pt[idx].x*pt[idx].x+(pt[idx].y-b[tc])*(pt[idx].y-b[tc]);
			if(x[0]<=x[i-1]&&x[i]<=x[sz])ans+=INT(x[i-1],x[i],B,C);
		}
	}
}
int main(){
	fastio;
	cin>>n;
	rep(i,1,n)cin>>pt[i].x>>pt[i].y;
	cin>>m;
	rep(i,1,m)cin>>a[i]>>b[i];
	work();
	rep(i,1,m)swap(a[i],b[i]);
	rep(i,1,n)swap(pt[i].x,pt[i].y);
	work();
	cout<<fixed<<setprecision(10)<<ans;
	return 0;
}