[笔记]字符串算法入门

字符串算法入门

​ ——Yoshinow2001
后缀系列和马拉车啥的还没学…以后再开一篇来更吧x

目录

• 字符串算法入门
  • 前置知识
  • 哈希表
    • 哈希表的引入
      • 例-解方程
    • 字符串哈希
      • 问题引入
      • BKDR哈希
      • 例-后缀字串&模式串LCP
      • POJ2774-最长公子串
      • CF580E——字符串周期
  • 单模式串匹配——KMP
    • 朴素算法
    • 数据冗余！
    • 最长公共前后缀
    • 复杂度分析
    • 相关练习
      • POJ2406-最短循环节
      • HDU6740-猜小数循环节
      • HDU2594-最长相同前后缀
  • 扩展KMP（Z函数）
    • 问题引入
    • Z函数和Z-box
      • 考虑性质
      • 代码实现
      • 复杂度？
      • 第二个问题呢？
    • 来道算法题！
      • CF526D
  • Shift-And/Or算法
    • 问题给出
    • 问题分析
    • 另一种字符串匹配方法
      • 朴素暴力
      • 优化算法
      • 核心代码：
  • 多模式串匹配——AC自动机
    • 问题引入
    • 例题
      • HDU2222-模板题
      • HDU2869病毒侵袭
      • HDU3065病毒侵袭持续中
      • POJ2778DNA-AC自动机+矩阵快速幂转移
      • JSOI有趣的游戏-AC自动机相关的概率问题
      • HDU2243考研路漫漫—单词情结-AC自动机+矩阵快速求和
      • 小总结
  • 资料索引

前置知识

大概是一些概念性的东西。

前缀：\(t=px\)，我们说\(p\)是\(t\)的一个前缀（prefix）

后缀：\(t=xs\)，我们说\(s\)是\(t\)的一个后缀（suffix）

匹配 ：给一个主串/文本串（text string）\(S=s_1s_2...s_n\)和一个模式串（pattern string）\(T=t_1t_2...t_m\)。在主串\(S\)中寻找模式串的过程叫字符串匹配，简称匹配，\(T\)称为模式。

ASCII码的可见字符

• 可见字符是从32开始一直到126，一共95个

哈希表

哈希表的引入

• 朴素地储存数据
  • 普通地用一个线性表储存数据\(a[1,...n]\)，查询某个数\(k\)会需要\(O(n)\)的时间
  • 用空间换时间，值域作为下标建立一个新的数组\(t[1,...m]\)，单次查询\(O(1)\)，但是空间开销可能非常大
• 哈希表
  • 考虑有这么一个哈希函数\(h(key)\)，例如\(h(key)=key\%23\)，如果能保证不同的\(key\)映射到不同的函数值，那就可以用\([0,...,22]\)来储存
  • 如果出现了哈希冲突，那就在这个下标位置建一个链表储存在这个位置，也可以考虑设计两个不同的哈希函数。嗯不过一般还是用第一种做法

struct node
{
    int nxt,info;
}hashNode[N];
int cnt;
int h[M];//头指针

inline void insert(int key,int info)
{
    int u=key%MOD;
    hash[tot]=(node){h[u],info};
    h[u]=tot++;
}

inline int find(int key,int info)
{
    int u=key%MOD;
    for(int i=h[u];i;i=hashNode[i].nxt)
    {
        if(hashNode[i].info==info)return 1;
	}
    return 0;
}

例-解方程

问题：已知\(x_1,x_2,x_3,x_4\)是\([-T,T]\)中的整数，问满足\(ax_1+bx_2+cx_3+dx_4=P\)的解有多少组？（\(T\leq 500\)）

题解：

• 枚举\(x_1,x_2,x_3\)确定\(x_4\)，复杂度\(O(n^3)\) ，TLE
• 枚举\(x_1,x_2\)，将计算结果\(P-ax_1-bx_2\)存到哈希表\(H\)里，再枚举\(x_3,x_4\),对应的结果\(cx_3+dx_4\)，在哈希表里查询是否出现过即可
• 时间复杂度\(O(n^2)\)

字符串哈希

问题引入

• 问题：有\(n\)个长度为\(L\)的字符串，问最多有几个字符串是相等的？
  • BruteForce：\(O(n^2L)\)
  • 哈希：如果能把一个字符串映射成一个值，一次映射\(O(L)\)，总的映射\(O(nL)\)，问题变成统计众数，总复杂度\(O(nL)\)
• 那么问题来了，哈希函数怎么设计？

BKDR哈希

• 选取适当的\(k\)，把一个字符串看成\(k\)进制数

  const int k=19;
  const int MOD=1e9+7;
  int BKDRhash(char *str){
      int ans=0,len=strlen(str+1);
      for(int i=1;i<=len;i++)
  		ans=(1ll*ans*k+str[i])%MOD;
      return ans;
  }
  

• 处理子串？

  for(int i=1;i<=len;i++)
      ha[i]=(ha[i-1]*k+str[i])%MOD;
  

  这样\(ha[i]\)就表示了\(str[1,...,i]\)的哈希函数值，对于一个询问\([l,r]\)，也就是要查找\(str[l,..,r]\)的哈希值。

  • \(ha[1,r]=s[1]k^{r-1}+s[2]k^{r-2}+...+s[r]k^0\)
  • \(ha[1,l-1]=s[1]k^{l-2}+s[2]k^{l-3}+...+s[l-1]k^0\)
  • \(ha[l,r]=s[l]k^{r-l}+s[l+1]k^{r-l-1}+...+s[r]k^0\)
  • 可以发现
    \[\begin{aligned} ha[l,r]=ha[1,r]-ha[1,l-1]k^{r-l+1} \end{aligned}\]

  • 所以可以\(O(log n)\)地查询，如果预处理了\(k\)的幂次，可以做到\(O(1)\)地查询子串的哈希值

• 不过当然，正确性其实并不能保证一定正确

例-后缀字串&模式串LCP

• 题意：给主串\(s\)和模式串\(t\)，长度\(2\times 10^5\)，有\(Q(Q\leq 2\times 10^5)\)个询问，每个询问给你一个\(x\)，问有多少个\(s\)的后缀子串和\(t\)的最长公共前缀长度恰好为\(x\)。
• Hash做法：
  • 注意到长度一共只有\(10^5\)量级，可以考虑用哈希搞一搞
  • 一共\(|s|\)个位置，对每个[后缀子串]二分[最长公共前缀长度]
  • 做完了…
  • 复杂度\(O(|s|log|s|)\)

POJ2774-最长公子串

• 题意：给两个字符串\(s,t(|s|,|t|\leq 10^5)\) ，求他们最长公子串的长度。
• （标算似乎是后缀xxx…但是这里数据范围比较小，就写个哈希的做法
• Hash做法：
  • 如果\(L\)是一个可能的最长公子串长度，那么\(L-1,L-2,...\)也是
  • 注意到这个单调性之后我们就可以二分答案来做啦。考虑如何检验一个答案\(x\)：\(O(|s|)\)地枚举\(s\)的所有长度为\(x\)的子串，记录Hash函数值，之后同样\(O(|t|)\)地枚举\(t\)的所有长度为\(x\)的子串，查询对应哈希值是否出现过，如果出现过我们就认为这个子串出现过。
  • 查询可以做一次\(O(nlog(n))\)的排序再进行二分查找。
  • 如果怕冲突也可以用双哈希或者链表来存。
  • 总的时间复杂度\(O(nlog^2n)\)，这题的数据范围还是能搞过去的（

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define rep(i,a,b) for(register int i=(a);i<=(b);i++)

typedef unsigned long long ull;
const int N=1e5+5;
const ull k=131;

int n,m;
ull hs[N],ht[N],p[N],temp[N];
int cnt;
char s[N],t[N];

inline ull get_s(int l,int r)
{
	return hs[r]-hs[l-1]*p[r-l+1];
}

inline ull get_t(int l,int r)
{
	return ht[r]-ht[l-1]*p[r-l+1];
}

inline bool check(int x)
{
	if(x>n||x>m)return 0;
	cnt=0;
	rep(i,1,n-x+1)temp[++cnt]=get_s(i,i+x-1);
	sort(temp+1,temp+cnt+1);
	
	rep(i,1,m-x+1)
		if(binary_search(temp+1,temp+cnt+1,get_t(i,i+x-1)))
			return 1;
	return 0;
}

int main()
{
	scanf("%s%s",s+1,t+1);
	n=strlen(s+1);m=strlen(t+1);
	
	int T=max(n,m);
	p[0]=1;
	rep(i,1,T)p[i]=p[i-1]*k;
	
	rep(i,1,n)hs[i]=hs[i-1]*k+s[i];
	rep(i,1,m)ht[i]=ht[i-1]*k+t[i];
	
	int l=0,r=min(n,m),res=0;
	while(r>l)
	{
		int mid=(l+r)>>1;
		if(check(mid+1))l=mid+1;
		else r=mid;
	}
	
	printf("%d",l);
}

CF580E——字符串周期

题意：给一个长度为\(n(n\leq 10^5)\)的字符串\(s\)，有两种操作：

• 1.将\([l,r]\)内的字符全部改为\(c\)
• 2.查询子串\(s[l,r]\)是否是一个以\(d(1\leq d\leq r-l+1)\)为周期的字符串

一个字符串\(s\)以\(d\)为周期当且仅当\(\forall 1\leq i\leq |s|-d:s_i=s_{i+d}\)

字符串周期

• 关于字符串的周期似乎一直是字符串问题里很经典的东西，如何高效判断一个字符串是否以\(d\)为周期是解决这题的关键。

• 首先明确定义，以\(d\)为周期并不要求\(d|(r-l+1)\)，例如\(1231\)就是一个以3为周期的字符串

• \(s[1,n]\)以\(d\)为周期当且仅当\(s[1,n-d]=s[1+d,n]\)

  • 必要性显然；
  • \([1,n-d]\)和\([1+d,n]\)相同，根据定义\(s_i=s_{i+d}\)可以看成把第\(i\)个字符右移\(d\)个位置之后和原字符仍然相同，也就是\(s[1,n-d]=s[1+d,n]\)

• 所以我们就可以把问题从整个区间的判定转换成判断两个区间的字符串是否相等

回到问题

查询操作转换成查询两个区间的哈希值是否相等，操作1就容易想到用线段树来维护区间赋值，用BKDR的哈希值也容易进行合并：

• 预处理出基数\(k\)的幂次\(1,k,k^2 ,...,k^n\) ，注意我们做区间覆盖\(c\)的时候有\(tr[node]=（c+ck+ck^2+...c^{r-l})=c(1+k+...+k^{r-l})\)，一种做法是\(O(log(n))\)地求出等比数列前缀和\(\frac{1-k^{r-l+1}}{1-k}\)，分母还需要求个乘法逆元，写起来麻烦点。
• 可以直接\(O(n)\)先预处理\(s[n]=\sum_{i=0}^n k^i\)，之后直接\(O(1)\)地查询
• 这样我们就完成了push_down 的实现

另一边我们需要注意一下查询区间哈希值时候的一些细节：

if(mid>=ql){
	if(mid+1<=qr)res=query(lson,l,mid,ql,qr)*p[min(qr,r)-mid]%MOD;
	else res=query(lson,l,mid,ql,qr);
}
if(mid+1<=qr)res=(res+query(rson,mid+1,r,ql,qr))%MOD;

如果当前区间的左右区间都可能有贡献，那样合并的时候左区间应该乘上一个\(k^{r-mid}\)，但是我们其实并不清楚实际的有区间是\(r\)还是\(qr\)（按照我这里的写法），所以这里取个min

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(register int i=(a);i<=(b);i++)

typedef long long ll;
const int N=1e5+5; 
int n,m,K;
ll tr[N<<2][2],tag[N<<2][2],k[2],MOD[2],s[N][2],p[N][2];
char str[N];

#define lson (node<<1)
#define rson (node<<1|1)

inline void push_up(int i,int node,int l,int r)
{
	int mid=(l+r)>>1;
	tr[node][i]=(tr[rson][i]+tr[lson][i]*p[r-mid][i])%MOD[i];
}

inline void push_down(int i,int node,int l,int r)
{
	if(tag[node][i]==-1)return;
	int mid=(l+r)>>1;
	tag[lson][i]=tag[rson][i]=tag[node][i];
	
	tr[lson][i]=(tag[node][i]*s[mid-l][i])%MOD[i];
	tr[rson][i]=(tag[node][i]*s[r-mid-1][i])%MOD[i];
	
	tag[node][i]=-1;
}

inline void build(int i,int node,int l,int r)
{
	tag[node][i]=-1;
	if(l==r)
	{
		tr[node][i]=str[l]-'0';
		return;
	}
	int mid=(l+r)>>1;
	build(i,lson,l,mid);build(i,rson,mid+1,r);
	push_up(i,node,l,r);
}

inline void modify(int i,int node,int l,int r,int ql,int qr,int w)
{
	if(ql<=l&&r<=qr)
	{
		tag[node][i]=w;
		tr[node][i]=w*s[r-l][i]%MOD[i];
		return;
	}
	push_down(i,node,l,r);
	int mid=(l+r)>>1;
	if(mid>=ql)modify(i,lson,l,mid,ql,qr,w);
	if(mid+1<=qr)modify(i,rson,mid+1,r,ql,qr,w);
	push_up(i,node,l,r);
}

inline ll query(int i,int node,int l,int r,int ql,int qr)
{
	if(ql<=l&&r<=qr)return tr[node][i];
	push_down(i,node,l,r);
	int mid=(l+r)>>1;
	ll res=0;
	if(mid>=ql)
	{
		if(mid+1<=qr)res=query(i,lson,l,mid,ql,qr)*p[min(qr,r)-mid][i]%MOD[i];
		else res=query(i,lson,l,mid,ql,qr);
	}
	if(mid+1<=qr)res=(res+query(i,rson,mid+1,r,ql,qr))%MOD[i];
	return res;
}

#undef lson
#undef rson

inline void init()
{
	scanf("%d%d%d",&n,&m,&K);
	scanf("%s",str+1);
	
	MOD[0]=19260817;
	MOD[1]=998244353;
	k[0]=233;k[1]=131;
	rep(j,0,1)
	{
		s[0][j]=p[0][j]=1;
		rep(i,1,n)
		{
			p[i][j]=p[i-1][j]*k[j]%MOD[j];
			s[i][j]=(s[i-1][j]+p[i][j])%MOD[j];
		}
	}
	build(0,1,1,n);build(1,1,1,n);
	rep(i,1,m+K)
	{
		int op,l,r,w;scanf("%d%d%d%d",&op,&l,&r,&w);
		if(op==1)
		{
			modify(0,1,1,n,l,r,w);
			modify(1,1,1,n,l,r,w);
		}else
		{
			ll r1,r2,t1,t2;
			if(w==r-l+1)r1=r2=t1=t2=1;
			else
			{
				r1=query(0,1,1,n,l,r-w);
				r2=query(0,1,1,n,l+w,r);
				t1=query(1,1,1,n,l,r-w);
				t2=query(1,1,1,n,l+w,r);
			}
			if(r1!=r2||t1!=t2)printf("NO\n");
			else printf("YES\n");
		}
	}
}

int main()
{
	init();
	return 0;
}

单模式串匹配——KMP

问题提出：给一个主串（文本串）\(S=s_1s_2...s_n\)和一个模式串\(T=t_1t_2...t_m\)，找到\(T\)在\(S\)中出现的所有位置。

朴素算法

最直接的暴力：对每一个\(i\)，从\(s[i]\)和\(t[1]\)开始逐个比较\(s[i]\)和\(t[1]\)，\(s[i+1]\)和\(t[2]\)…，如果出现了失配（即某个\(j:s[i+j-1]\neq t[j]\)）那就从\(s[i+1]\)开始从头匹配。时间复杂度\(O(nm)\)

数据冗余！

不妨手动模拟一下暴力匹配的过程：（这似乎也经常是需要优化一个算法但无从下手的时候一个很好的入手点，尝试手动模拟小范围数据看看有哪些东西是可以优化的）

s=abababcabca

t=abc

（这里就不展示具体的模拟过程了x）

有这么几个问题：如果\(t\)匹配到了某个位置\(j\)而在\(j+1\)处出现了失配，我们就把\(i\)变成\(i+1\)，而\(j\)重置到1，这样子是不是没有利用好当前所有的信息？字符串匹配到了\(j\)意味着\(s[i-j+1,i]=t[1,j]\)

我们的\(j\)指针可不可以不用重置到1？或者说这前\(j\)个字符正确的匹配是否能给我们一些额外的信息让我们能把整个\(t\)整个串多右移一点？

如果我们能找得到\(t\)的一个前缀\(t[1,x]\)和\(t[1,j]\)的一个后缀\(t[j-x+1,j]\)相等，那么前\(j\)个字符匹配成功就意味着\(s[i,i+j-1]=t[j-x+1,j]=t[1,x]\)，因此我们可以直接把\(t\)串右移很大一段！（即失配之后把\(j\)重置为\(x\)继续进行比较，而非重置为1）

这里先给出数组nxt[]，其中nxt[x]表示模式串\(t[1,x-1]\)的最长公共前后缀，则我们可以给出KMP算法的部分代码：

for(int i=2,j=0;i<=n;i++){
	while(j&&s[i]!=t[j+1])j=nxt[j];
    if(s[i]==t[j+1])j++;
    if(j==m)
    {
        //Match!
        j=nxt[j];
	}
}

下面的问题就是如何高效求解nxt[]数组啦！

最长公共前后缀

根据前面的思路，我们需要比较快的预处理出模式串\(t\)的每个前缀\(t[1,x]\)的最长公共前后缀。

定义：对于一个字符串\(s\)，\(s[1,x]=s[r-x+1,r]\)的最大\(x\)称为\(s\)的最长公共前后缀长度

nxt[1]=0;
for(int i=2,j=0;i<=m;i++)
{
	while(j&&t[i]!=t[j+1])j=nxt[j];
    if(t[i]==t[j+1])j++;
    nxt[i]=j;
}

（其实就是让\(t\)自己和自己做一次匹配）

复杂度分析

以求\(nxt[]\)数组的过程为例，注意到几件事情：

• 每次循环\(j\)至多加一，\(i\)一定加一，一定有\(j<i\)成立，因此\(j\)至多增加\(m-1\)次
• while循环要触发，\(j\)一定非负，而又有\(nxt[j]<j\)，每次触发一定会让\(j\)至少减少1
• 而\(j\)至多增加\(m-1\)次，因此也至多减少\(m-1\)次，这一段\(while\)循环也至多被执行\(m-1\)次
• 结合外面一个\(for\)循环，整个\(nxt[]\)的求解的复杂度是\(O(m)\)

同理可以知道两个字符串匹配的时间复杂度是\(O(n+m)\)的，整个算法复杂度\(O(n+m)\)

相关练习

（似乎许多题目都是在考nxt[]数组的应用

POJ2406-最短循环节

题意：给一个字符串\(|s|\)，记求其最短循环节\(e\)的长度\(|e|\)， 求\(|s|/|e|\)，其中\(s=\underbrace{eee..eee}_{若干个}\)。\(|s|\leq 10^6\)

做法：注意nxt[]数组的意义：nxt[n]表示\(s[1,n]\)的最长公共前后缀长度（同时保证\(nxt[x]<x\)），记\(k=nxt[n]\)，计算\(t=n-nxt[n]\)，如果\(t|n\)则\(t\)是一个最短循环节，否则最短循环节只能是\(n\)了。

HDU6740-猜小数循环节

HDU2594-最长相同前后缀

题意：给两个字符串\(s,t\)，求长度最长的串，满足既是\(s\)的前缀又是\(t\)的后缀，\(|s|,|t|\leq 5\times 10^4\)。

做法：

容易想到\(nxt\)数组…两个字符串拼起来，注意中间接一个间隔符隔开，否则可能会出现答案大于\(|s|,|t|\)的情况

扩展KMP（Z函数）

问题引入

（洛谷5410模板题）

问题：有两个字符串\(S,T\)，希望求出两个数组:

• \(T\)的\(Z\)函数数组：\(Z[i]\)表示\(T[1,|T|]\)与\(T[i,|T|]\)的LCP（最长公共前缀）的长度
• \(T\)与\(S\)的每一个后缀\(S[i,|S|](i=1,2,..,|S|)\)的LCP长度

Z函数和Z-box

（orz暂时直接给出整个\(Z\)函数的定义和构造方式，原理以后有空再来填坑）

• 定义题目已经给我们了，嗯那就直接拿来用吧。我们用\(z[i]\)表示\(T[1,|T|]\)和\(T[i,|T|]\)的LCP长度，也就是一个字符串和他自己一个后缀的最长公共前缀的长度！啊听起来好绕啊（

• 嗯说得好，那怎么求这个东西？和KMP算法一样，我们同样尝试能不能找到一些性质：根据\(Z\)函数的定义，如果我们已经有了一些前缀的\(Z\)函数\(Z[1],Z[2],...Z[i-1]\)，有没有办法比较快地求出\(Z[i]\)？

• 首先有\(Z[1]=|T|,\)嗯很好！接着往下呢？好像要跑个暴力…

考虑性质

既然我们定义了这个奇怪的\(Z\)函数，那就稍微用一下吧?根据定义：如果我们得到了一个\(Z[i]\)，那自然就有\(T[1,Z[i]]=T[i,i+Z[i]-1]\)成立（如图所示，两块蓝色的区域是相同的）

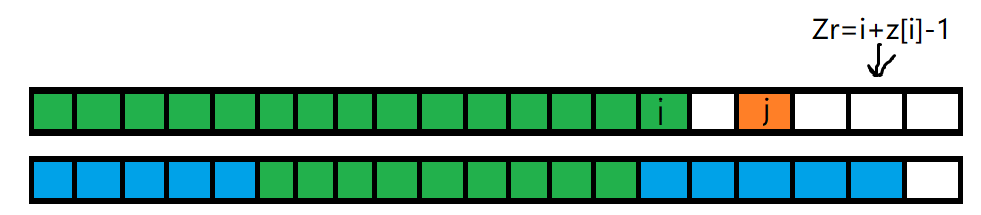
我们从左往右扫，记录下当前最大的\(Z_r=i+Z[i]-1\)，既然两块蓝色的区域相同，那他们的子区间自然也相等。于是我们就联想到能不能利用这一关系来快速求解\(1<j\leq Z_r\)的\(j\)。接着往下想，要想满足这一关系，我们还得在记录\(Z_r\)的时候连着记录\(Z_l=i\)，在递推接下来的\(j\)时我们计算右边蓝色区间的\(j\)对应在左边蓝色区间的位置\(j'=j-Z_l+1\)，这个位置一定是求过了的，那么我们自然能得到\(Z[j']\)的值，如果\(j'+Z[j']-1\leq Z[i]\)，即\(j'\)对应的\(Z_r'\)也被包含在我们左边蓝色区间里面，稍微整理一下，我们有这些信息：

• \(T[1,Z[j']]=T[j',j'+Z[j']-1]\)（由\(Z[j']\)定义得到)
• 而由\(j'+Z[j']-1\leq Z[i]\)知道\(T[j',j'+Z[j']-1]=T[j,j+Z[j']-1]\)（蓝色区间相同）
• 进一步把两个等式连起来\(T[1,Z[j']]=T[j,j+Z[j']-1]\)
• 所以根据定义，就有\(Z[j]=Z[j']\)啦！！！

（废话那么多x不如直接看图)

！！所以对于\(j\leq Z_r\)并且\(j+Z[j-Z_l+1]\leq Z_r\)的情形，我们可以\(O(1)\)地\(Z[j]=Z[j-Z_l+1]\)啦

嗯，那其他情况呢，比如\(j\leq Z_r\)但是\(j+Z[j-Z_l+1]>Z_r\)了？那至少会有\(Z[j]\geq Z_r-j+1\)吧，还是因为区间相等。剩下的直接暴力…

要是\(j>Z_r\)呢？那我们回到前面，暴力求\(Z[j]\)然后更新一下\(Z_l,Z_r\)就好啦！

代码实现

这一段代码写起来大概就算这样：

z[1]=n;//n is the length of string T
zl=zr=0;
for(int i=2;i<=n;i++){
    if(i>zr){
        while(i+z[i]<=n&&t[1+z[i]]==t[i+z[i]])z[i]++;
        zl=i;zr=i+z[i]-1;
    }else{
        if(i+z[i-zl+1]<=zr)z[i]=z[i-zl+1];
        else{
            z[i]=zr-i+1;
            while(i+z[i]<=n&&t[1+z[i]]==t[i+z[i]])z[i]++;
            zl=i;zr=i+z[i]-1;
        }
    }
}

还是挺简洁哒

• 哦对了，说好的Z-box呢？
• 上面的\([Z_l,Z_r]\)就叫Z-box啦…

复杂度？

搞了这么多幺蛾子要是复杂度还是\(O(n^2)\)怎么行（

对于暴力匹配的情况，每个字符最多和前缀成功匹配一次（就算有两处暴力匹配，但是第二处我们直接从\(Z_r\)开始往后匹配了，所以也不会有重复的操作）。所以最关键的两个暴力匹配的地方其实加起来都是\(O(n)\)的，所以整个算法复杂度自然也是优秀的\(O(n)\)辣！！

第二个问题呢？

字符串问题的一个常用操作：两个串拼起来！

具体来说我们要\(T\)的前缀和\(S\)的后缀，那就把构造\(T'=T+'@'+S\)，中间的\('@'\)应该是一个不在\(T,S\)中出现的字符。接着我们利用\(1,..,|T|\)的\(Z[]\)函数去继续推就行啦。

来道算法题！

CF526D

题意：给定字符串长度\(n\)和常数\(k\)，和一个字符串。要求对每个前缀判断，这个前缀是否能被写成\(S_i=\underbrace{A+B+A+B+...+A}_{k+1个A，k个B}\) 的形式，允许\(A,B\)有一个为空。

题解：

和其他字符串题一样，尝试把这个麻烦的条件转化成别的东西：这个交替排列比较麻烦，我们手上并没有什么东西能处理，但是注意到\(k\)是给定的，而前面的\(k\)对的\(AB\)可以看成一整块，所以似乎能把前面一部分看成是一个以\(|AB|\)为周期，重复\(k\)次的一个字符串，最后的\(A\)则是\(AB\)的一个前缀。

嗯？似乎能给出一个粗糙的思路：对于一个位置\(i\)，好像可以判断它左边的东西是否有周期\(T\)（这个\(T\)我们容易算出）再往右边找这个后缀和字符串前缀的LCP长度，长度和\(T\)取个最小值，那样从\(i\)往右到\(min(T,z)\)的一段区间就都是符合条件的。而LCP长度对应Z函数的值，可以\(O(n)\)求解，而对于一个前缀\(S\)判断是否有周期\(T\)，可以转换成判断是否有\(S[1,(k-1)T]=S[T+1,kT]\)，进一步转换成是否有\(Z[T+1]\geq(k-1)T\)。（注意这里并不是用\(nxt[]\)数组来做，next数组求出的是最小的那一个周期，而此处要求的\(T\)并不需要是最小的）

代码实现：

（之前另一种写法莫名就挂了x）

（区间赋值可以改成对差分序列做单点修改，最后统计前缀和被加了多少次）

for(register int i=1;i*k<=n;i++){
    if(z[i+1]<(k-1)*i)continue;
    s[i*k]++;
    s[i*k+min(i,z[i*k+1])+1]--; 
}
int now=0;
rep(i,1,n){
    now+=s[i];
    printf("%d",(now>=1?1:0));
}

Shift-And/Or算法

• 吐槽：前两天打组队赛遇到一个字符串的题考了这个（见：http://acm.hdu.edu.cn/showproblem.php?pid=5972）…当时写了个KMP瞎搞然后TLE了（害），赛后去查了许多资料似乎就看见一个题考了这么个鬼东西…

问题给出

• 给一个主串\(S=s_1s_2...s_n\)和一个模式串\(T=(t_{11}|t_{12}|...|t_{1k_1})(t_{21}|t_{22}|...t_{2k_2})...(t_{m1}|t_{m2}|...|t_{mk_m})\)，对于\(S\)的一个子串\(S'[1,m]=S[i,i+m-1]\)，只要第\(j\)个位置满足\(S[j]=t_{j1},t_{j2},..t_{jk_j}\)中的其中一个，就算匹配成功。找到\(S\)中所有能和\(T\)匹配的子串。
• \(|S|,|T|\)的范围依然很大，\(k_i\)和字符集比较小

问题分析

• 首先想到的是去修改一下KMP里匹配成功的条件…如果在一个位置发现了失配，即\(s[i]\not\subset t[j+1]\)，那样我们希望仍然有一个合适的失配数组\(nxt[]\)让我们跳回合适的位置，即找到一个\(T[1,j]\)的最长公共前后缀跳回去，但是这里就出现了问题，如果要保证\(S\)匹配到的后缀要和新的\(T\)的前缀匹配，那就得保证我们找的\(T\)的这个前缀包含了\(T\)的后缀，可是这样就也要改掉\(nxt[]\)数组的求解。
• 好那就改吧，构造失配数组的时候把匹配条件t[i]==t[j+1] 改成包含关系，即我们要让\(T[1,j+1]\)这个前缀包含\(T[i-j,i]\)这个后缀如果\(k_i\)小的话这一步仍然可以认为是\(O(1)\)的时间，整个处理过程仍然是\(O(|T|)\)的。嗯到这里感觉都不错，接下来进行两个字符串的匹配了，\(S\)和\(T\)的比较也改成比较是否包含。如果失配的话同样是\(j=nxt[j]\)地往回跳，一直到\(j==|T|\)匹配成功…到这里似乎都没什么问题
• 但是但是…一旦匹配成功输出结果，\(j\)这个指针该怎么跳？\(j=nxt[j]\)？但是很快就会发现这里这样做会漏掉一些情况…（因为如果要求【跳到的前缀包含了当前的后缀】这样一个苛刻的条件，那样可能会出现\(S\)串马上又可以匹配，但是我们条件太苛刻跳过了的情况）
• 想来想去没法解决这个问题…
• 好吧既然KMP没法解决…不如我们换个算法（逃

另一种字符串匹配方法

和其他算法问题一样，我们可以考虑换一个维护的对象。下标，字符集…

比如这里，我们考虑从另一个角度切入字符串匹配的问题：对于字符集比较小的匹配，对模式串\(T\)里每个字符出现的位置进行记录：即用一个数组\(B[i][j]\)表示字符\(i\)在第\(j\)个位置是否出现。这样记录能够处理这题里令我们头疼的问题：模式串的一个位置允许多种取值。

朴素暴力

好了现在有了这么一个想法，先试试看最暴力地要怎么做这个问题

（约定|S|=m,|T|=n）

\(O(n)\)地求出\(B[][]\)数组

for(int i=1;i<=n;i++)
	int k;scanf("%d",&k);
    for(int j=1;j<=k;j++)
		int t;scanf("%d",&t);
		B[t][i]=1

每次暴力匹配\(S\)和\(T\)，时间复杂度还是\(O(nm)\)

for(int i=1;i<=m;i++)
    int j=1;
	for(;j<=n&&B[s[i+j-1]][j];j++);
    if(j==n+1)
    	match!

优化算法

和其他字符串算法的思路一样，我们尝试能不能通过维护一些前后缀的信息来减少信息的冗余：比如这里我们发现，上面的算法每次都在暴力\(O(n)\)地比较\(S[i,i+n-1]\)和\(T[1,n]\)，我们可以把这个过程看成\(S[1,i+n-1]\)的后缀和\(T[1,n]\)的前缀进行比较，于是类似KMP的思路，也许我们可以去维护\(S\)的后缀和\(T\)的前缀相关的信息！（这就是Shift-And算法的思路！）

我们考虑再用一个数组\(D[]\)来维护这样一个信息：\(D[j]=1\)当且仅当\(S[i-j+1,i]\)和\(T[1,j]\)匹配，即\(S\)的一个后缀是\(T\)的前缀。否则\(D[j]=0\)。马上我们将会发现用Bool类型储存这样一个信息的优越性。

如果我们让\(i,j\)两个指针一起跑（如图），能写出递推式：\(D[j+1]=(D[j])\&(S[i+1]==T[j+1])\)。进一步我们利用前面做好的数组\(B[][]\)，可以把相等的判定修改一下，变成：\(D[j+1]=D[j]\&B[S[i+1]][j+1]\)

到这里都还只是逐位地进行位运算的比较，但是我们注意到这个\(D[]\)似乎可以做成一个\(bitset\)，把它看成是一个长度为\(|T|\)的二进制数的话，尝试直接用一个\(D\)表示这个数组，用位运算来实现这个递推。

考虑上面的过程，从\(D[j]\)到\(D[j+1]\)需要先把上一位\(D[j]\)的信息复制过来，再对\(j+1\)位进行一个取\(\&\)的操作，考虑从\(i=1,j=1\)往上递推的整个过程…对于每个\(i\)，每次遍历\(1,2,3,...,j...,|T|\)，复制信息…对应位置取\(\&\)，这个复制信息的过程不就相当于把一个二进制数全部左移一位么？每次取\(\&\)也很麻烦，我们把\(B[i][j]\)的第二个维度也压掉，直接对两个二进制数按位\(\&\)，同时为了保证\(\&\)正确性，每次左移完了之后把最低位赋为1。

另外，对于超过\(|T|\)的\(j\)的信息我们可以直接丢掉，所以也不用担心丢失什么信息。

至此，我们已经可以抛去\(j\)这个指针，得到从\(i\)到\(i+1\)递推式：

\(D=(D<<1|1)\&B[S[i+1]]\)实现

核心代码：

const int N=5000005;
const int M=1005;

char s[N];
char t[M];
bitset<M>B[10],D;
int n,len;

int main(){
	scanf("%d",&n);
	rep(i,1,n){
		int k;scanf("%d",&k);
		rep(j,1,k){
			int t;scanf("%d",&t);
			B[t].set(i,1);
		}
	}
	
	scanf("%s",s+1);
	len=strlen(s+1);
	rep(i,1,len){
		D=(D<<1).set(1)&B[s[i]-'0'];
		if(D[n]){
			char ch=s[i+1];
			s[i+1]=0;
			puts(s+i-n+1);
			s[i+1]=ch;
		}
	}
    return 0;
}

多模式串匹配——AC自动机

问题引入

同样是给定一个文本串\(S\)，和\(n\)个模式串\(T_1,T_2,...,T_n\)，\(n\leq 10^5,\sum|T_i|\leq 2\times 10^6\)

懒得写了。

注意做匹配的话加个拓扑序优化，最后更新答案，不然会被卡到平方的复杂度

例题

zyz学长的题单：http://molihua.fzu.edu.cn/icpc/person/031802540/string

（代码好长不贴了）

HDU2222-模板题

懒得写，大水题

HDU2869病毒侵袭

AC自动机裸题，注意输出格式最后一行换行…

HDU3065病毒侵袭持续中

多组数据…

POJ2778DNA-AC自动机+矩阵快速幂转移

题意：给\(m\)个DNA片段（仅包含ATCG）（\(m\leq 10\)），长度不超过10，给一个数\(n\)，问有多少个长度为\(n\)的DNA序列（仅包含ATCG），不包含这些DNA片段。

题解：

• 一开始倒着想反而想不出来…其实根本没必要…

经典套路：涉及到某些给定长度，要求包含或者不包含某个串的操作，以及涉及到字符串的计数，大概能往这边想。

比如这题，建AC自动机，把从一个长度为\(k\)的串扩展到\(k+1\)的串的过程看成在自动机上走一步的过程，只要走的边都是合法的，那样最后得到的串就是合法的。这里至多100个节点，建一个邻接矩阵跑矩阵快速幂，统计根节点（起点）到所有点（包括自己，因为如果自动机上没有边的话转移到根节点也是合法的）的方案数就是总答案。

而判断哪些点是合法也好做，自动机的叶子结点一定是非法的，同时还要注意！可能会有相互包含的状态，所以如果有某个点\(x\)的孩子\(tr[x][i]\)，还要看一下\(tr[fail[x]][i]\)这个结点是否是一个叶子结点（因为\(tr[fail[x]][i]\)一定是\(tr[x][i]\)的一个后缀，如果这个后缀非法那这个串自然也是非法的）。

最后注意这题卡常数！

取模运算比较慢。跑矩阵快速幂的时候做完乘法取模两次会被卡掉：

rep(i,0,m1.size)rep(j,0,m1.size)
{
    res.s[i][j]=0;
    rep(k,0,m1.size)
    {
        res.s[i][j]+=m1.s[i][k]*m2.s[k][j]%MOD; //这个要删掉才行…
        res.s[i][j]%=MOD;
    }
}

JSOI有趣的游戏-AC自动机相关的概率问题

题意：\(n(n\leq 10)\)个人玩游戏，第\(i\)个人一开始有个字符串\(T_i,|T_i|\leq 10\)，同时字符集\(|\Sigma|\leq 10\)，有一个机器每次以一定概率生成字符集中的某个字母（概率给定），机器不断生成字符组成一个字符串，一旦生成的字符串是某个人手上字符串的子串，这个人获胜，同时游戏结束。求每个人获胜的概率。

题解：

和前面一样，涉及到这种不断生成字符串以及子串关系的题目我们容易想到AC自动机和用矩阵转移状态。

一样的套路，把所有人的字符串建一个AC自动机，结尾打上编号，至多100个结点，接着还是建邻接矩阵。

这里我们用\(M[i][j]\)表示从结点\(i\)转移到\(j\)的概率，

• 对于一个叶子结点（到达这里即代表这个玩家赢了），直接让\(M[i][i]=1\)，也就是此时玩家胜利，并且这个\(i\)就不能再连到别的边了，因为游戏结束了。

• 否则其他结点我们让\(M[i][tr[i][j]]\)加上\(p[j]\)，注意不是直接赋值，因为一个Tire图里其实有许多没匹配的边会直接跳到\(fail\)上，所以可能会出现自动机在某个状态\(x\)接收到的好几种字符\(c\)之后都要转移到同一个结点，如果直接赋值显然就会出问题

• 还有一个注意点就是如何根据这个概率矩阵来做状态转移啦，容易想到让矩阵\(M\)自乘许多次：

for(int i=1;i<=100;i++)M=M*M;

这样子求出来的是\(M^{2^{100}}\) ，（如果只是\(M^k\)写快速幂的话似乎精度都不太够）

HDU2243考研路漫漫—单词情结-AC自动机+矩阵快速求和

老AC自动机了（

题意：给\(n(n\leq 6)\)个模式串，仅包含小写字母，长度不超过5，给一个\(L(L\leq 2^{31})\)，问有多少个仅由小写字母组成的长度不超过\(L\)的字符串至少包括1个模式串

题解：

（怎么数据范围一题比一题小…）

• 先理思路

至少包括1个模式串这个条件应该容易转化成总字符串数减去不包括任何模式串的字符串数

直观上总字符串数比较好统计，这里要注意原问题要计数的东西是包括模式串的字符串，所以这里的“总字符串”的长度应该不小于\(min_{i}\{|T_i|\}\) 才行。也就是如果我们记\(t=min_{i}\{|T_i|\}\)，总字符串数=\(26^t +26^{t+1} +...+26^L\)，这样总字符串数的式子就列出来了。

不包含任何模式串的字符串数呢？类似之前DNA那道题，用模式串建一个AC自动机，所有叶节点和以某个叶节点作为后缀的结点都打上标记，保证随便怎么走都不会走到一个模式串的结尾。再根据得到的图建一个转移矩阵\(M\)，最后求\(res=M^{t}+M{t+1} +...+M^{L}\)，再对\(res[0][i]\)统计即可（其实如果记\(G(M)\)为\(M\)第0行的和，这个做法其实上是\((26^{t} -G(M^{t})) +...+(26^{L} -G(M^{L}))\)来着的），然后我们把式子拆开来做了。

嗯到这里似乎一切都令人满意。

• 问题来了

这个前缀和怎么求来着…

嗯？（思考…）

\(A^4=(A+A^2 )A^2 +(A+A^2)\)

\(A^5 =A*A^4 +(A+ A^2 +A^3 +A^4)\)

\(A^6=(A+A^2) A^4 +(A+A^2 +A^3 +A^4)\)

然后似乎能给出下面的代码：

inline Mat sum(Mat A,ull b){
	Mat p=A,res;
	rep(i,0,cnt)rep(j,0,cnt)res.s[i][j]=0;
	for(;b;b>>=1){
		if(b&1)res=p+A*res;
		p=p+A*p;
		A=A*A;
	}
	return res;
}

另一边求前缀和也一样的做…

这题就解决啦…

• （顺便，多组数据，清理数据的时候一定要清理干净…，初始化写清楚orz）
• （顺顺便：
  

小总结

• 涉及到匹配的问题写上拓扑序优化，不然会被卡。
• 涉及到子串问题，包含/不包含字符集\(T\)的计数问题，考虑Tire图上的状态转移，计数就用图论里计数的方法来计数。
• 一些奇怪的字符串问题如果数据范围很小只有几十的话可以瞎猜用矩阵来建模
• 需要特别注意模式串集的包含关系。
• 对于那些涉及到类似无限、直到某个人获胜时结束的问题，也可以转化成矩阵上的问题，让矩阵不断自乘最后答案会收敛到某个值，同时要注意乘的次数要足够多。

资料索引

• 书籍
  • 《算法导论》第三版32章
• 网络资料
  • KMP
    • https://www.zhihu.com/question/21923021
    • https://blog.csdn.net/yyzsir/article/details/89462339
  • 扩展KMP(Z函数)
    • https://www.cnblogs.com/ycx-akioi/p/Z-algorithm.html
  • Shift-And,Shift-Or
    • https://www.cnblogs.com/longdouhzt/archive/2011/09/25/2190550.html
    • https://blog.csdn.net/silence401/article/details/77446537
    • http://en.volupedia.org/wiki/Bitap_algorithm