[小专题]栈与表达式求值

划水&摸鱼了好多天…解决了高中一直没搞清楚的表达式求值的内容…

写篇博客记录一下

---

 

 

1.栈（Stack）

---

 

 

 

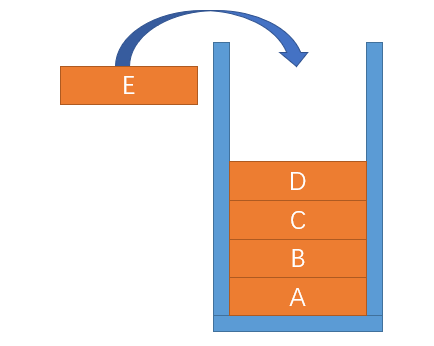
直观理解 如图所示，类似于厨房用来放调羹的那个槽…先放进去的会被压在底下，一般叫做栈底（bottom）元素，最后进去的则作为栈顶（top）元素，我们把一个调羹放到槽里面就叫做把这个元素压入（push）栈里，把顶部的调羹拿出来就叫做把一个元素从栈中弹出（pop），栈相关的操作基本就是这些，C++的STL也自带了stack类型，声明形式为 stack<type>s; ,type是要插入栈的元素类型。使用时只要include头文件stack就可以调用啦

当然我们自己也容易用数组实现一个确定空间上界的栈：

struct Stack
{
    ll s[N],cnt;
    Stack()
    {
        cnt=0;
        memset(s,0,sizeof(s));
    }
    inline ll top(){return s[cnt];}
    inline ll pop(){return s[cnt--];}
    inline void push(ll x){s[++cnt]=x;}
    inline bool empty(){return (cnt==0);}
};

C++自带的栈当然方便啦，不过在算法竞赛中可能为了常数小一些经常会选择手写栈

 

2.概念补充：表达式、运算符、表达式树

---

 

不出意外的话屏幕前的你是一个人类（？），人类们似乎能比较容易地判断类似于$2+3*5^2-3*(5+2)$这样的表达式（notation）要先计算谁后计算谁，但是现在我们想让计算机帮我们做运算，自然要设计一套算法让计算机能够知道先计算谁后计算谁。也就是我们希望能建立一套成系统的方法，把一个记录表达式的字符串拆成若干个元素，运算对象（operand）归操作对象，运算符（operator）归运算符，最好再把运算符的优先级处理好。

首先明确一下优先级：遇到括号应该先算括号内的，括号内的优先级最高，然后是幂运算>乘除>加减。

需要注意的是通常情况下优先级相同的从左到右左边的先算（比如6*3/2一般会认为先算乘法后算除法）

但是常用的运算符有个比较特殊的：幂运算，比如2^3^4我们通常会理解为是2^(3^4)而不是(2^3)^4。

于是对于+-*/这类运算符我们就说他是左结合的（Left-Associativity），而像幂运算^这类运算符我们就说它是右结合的（Right-Associativity），这些概念会在下面用到。

表达式树同样不陌生，对于每个表达式我们选择一个优先级最低的运算符作为树根，运算符的左右两边作为左右子树，左右子树再进行同样的操作，例如上面的表达式可以构建如下的表达式树：

 

 

 对这颗二叉树进行前种后序遍历可以分别得到原表达式的前缀（prefix）、中缀（infix）、后缀（postfix）表达式

而后缀表达式则又被成为逆波兰表达式（reverse Polish notation），前缀表达式也被成为波兰表达式。

 

3.调度场算法（shunting-yard algorithm）

---

 

例子中的2+3*5^2-这部分，先读到运算对象2和运算符+，接着是3，这里我们不能急着做加法，原因是不知道后面有什么，所以这里正确的操作应该是先把“这里有个加法运算”这件事存起来，同时最好运算对象也被按顺序存好。接着往下我们发现一个乘法，同样不知道后面会不会有优先级更高的运算，同样存起来。好的我们读到了“^”，它比乘法优先级更高，继续往下读读到一个减法，优先级比当前的幂运算低，这意味着前面的部分可以开始算了。

现在开始倒着进行运算：因为我们都是保留优先级低的操作，所以到此为止的运算符优先级都是单调递增的，也就是要对靠后的运算符先进行操作，同样对于运算对象也是，基于这点我们联想到用栈来做这件事。

栈S1储存数字，栈S2储存运算符，到这里S1的元素分别是：2,3,5,2，而S2的元素分别是：+，*，^，取出S2的一个幂运算和S1的2和5，注意顺序是倒着来的，所以应该是以5为底，求得5^2，

再把计算结果25压入S1，接下来的操作类似，S1有2,3,25，S2有+，*，取出乘法和25和3，计算结果3*25=75压入S1，继续取出S2的+和S1的75和2，计算结果2+75压入S1，直到S2变空，这时候S1剩下的一个元素就是运算结果

得到一个简单的伪代码：

while there are tokens to be read:
    read a token.
    if(the token is an operator)
    	while((S2 not empty)and(precedence of the top of S2>=precedence of this operator))
    		calculate
		push the operator onto S2
　　 else
	//the token is an operand
	push it onto S1
while(S2 not empty)calculate
print the top of S1

 

括号怎么处理？

括号优先级最高，遇到左括号先存起来，进行calculate则需要额外加一个S2的top不是左括号

如果读到左括号直接压到运算符栈S2，如果读到右括号则一直进行计算直到读到左括号，最后再把左括号扔掉。

（因为括号内能先算的其实都已经算了，所以只会剩下优先级单调不减的运算符，直接算就行）

 

左结合和右结合？

如果S2栈顶元素和当前运算符优先级相同且都是右结合的（比如^），那也不能进行运算，也就是把

precedence of the top of S2>=precedence of this operator

稍微修改一下变成

(precedence of the top of S2>precedence of this operator)or((precedence of the top of S2==precedence of this operator)and(this operator is not Right associativity))

 

到此为止代码就差不多成形了：

//n is the length of string str
//pre[x] records the precedence of operator x
//calc() is the function calculating
for(register int i=1;i<=n;i++)
{
    if(oper(str[i]))
    {
        while(!S2.empty()&&oper(S.top())&&((pre[S2.top()]>pre[str[i]])||(pre[S2.top()]==pre[str[i]]&&str[i]!='^'))&&S.top()!='(')
            calc();
        S2.push(str[i]);
    }else if(str[i]=='(')
    {
        S2.push(str[i]);
    }else if(str[i]==')')
    {
        while(S2.top()!='(')calc();
        if(S2.top()=='(')S2.pop();
    }else if(num(str[i]))
    {
        ll sum=0,j=0;
        for(;num(str[i+j]);j++)sum=sum*10+str[i+j]-'0';
        i+=j-1;
        S1.push(sum);
    }
}
while(!S.empty())calc();

 

上面这个算法就是标题的调度场算法shunting-yard algorithm啦，是Dijkstra大佬提出的~算法的起名大概是因为这个原理很像下图的结构：

↑图转自Wikipedia

 

4.和逆波兰表达式的关系

---

 

不难发现如果把计算改成输出运算符，把压入数字改成输出数字，就得到了原来表达式的逆波兰表达式啦。

而逆波兰表达式的计算也很简单，省去了对优先级的考虑——读到运算符就对前两个数字进行运算，就能够给出答案

 

5.来道题！

---

Luogu2379：给若干个单项式或者多项式，包含+、-、*、和^，字母只包括小写字母，输出运算结果

 

话说这题我没A，因为我写了个用set维护多项式字典序的东西…后面发现只要保证每个项按字典序排序，多项式直接按照输入顺序输出就行了…然后我懒得改（

表达式计算的框架和上面一样，对于每个项我选择用一个27个元素的数组s[]记录，s[0]记录前面的系数，s[1]到s[26]分别表示a到z的次数，然后再用一个set储存每个项，手写一个比较函数来维护多项式字典序。

加减乘法再手写一下~就得到一个挺长的代码啦…

#include<cstdio>
#include<set>
#include<stack>
#include<cstring>
using namespace std;
#define rep(i,a,b) for(register int i=(a);i<=(b);i++)

typedef long long ll;

const int N=300;

//term
struct term
{
    ll s[27];
    term(){memset(s,0,sizeof(s));}
    inline void print()const
    {
        if(s[0]!=1)printf("%d",s[0]);
        rep(i,1,26)if(s[i])
        {
            printf("%c",'a'+i-1);
            if(s[i]>1)printf("^%d",s[i]);
        }
    }
};

struct cmp
{
    inline bool operator () (const term &A,const term &B)
    {
        rep(i,1,26)if(A.s[i]!=B.s[i]){return A.s[i]>B.s[i];}
        return 0;
    }
};


inline term operator * (const term &A,const term &B)
{
    term C;
    C.s[0]=A.s[0]*B.s[0];
    rep(i,1,26)C.s[i]=A.s[i]+B.s[i];
    return C;
}

inline bool check(term A,term B)
{
    rep(i,1,26)if(A.s[i]!=B.s[i])return 0;
    return 1;
}

inline term operator +(term A,term B)
{
    term C;
    C.s[0]=A.s[0]+B.s[0];
    if(C.s[0]==0)return C;
    rep(i,1,26)C.s[i]=A.s[i];
    return C;
}

inline term operator -(term A,term B)
{
    term C;
    C.s[0]=A.s[0]+B.s[0];
    if(C.s[0]==0)return C;
    rep(i,1,26)C.s[i]=A.s[i];
    return C;
}

//polynomial 

struct P
{
    set<term,cmp>p;
    inline void insert(const term &A)
    {
        set<term,cmp>::iterator itr=p.begin();
        bool b=1;
        for(;itr!=p.end();itr++)
        {
            if(check(*itr,A))
            {
                term temp=*itr;
                temp=temp+A;
                p.erase(itr);
                p.insert(temp);
                b=0;
                break;
            }
        }
        if(b)p.insert(A);
    }
};

inline P operator +(const P &A,const P &B)
{
    P res=A;
    
    for(set<term,cmp>::iterator itr=B.p.begin();itr!=B.p.end();itr++)res.insert(*itr);
    
    return res;
}

inline P operator -(const P &A,const P &B)
{
    P res=A;
    P t;
    for(set<term,cmp>::iterator itr=B.p.begin();itr!=B.p.end();itr++)
    {
        term temp=*itr;
        temp.s[0]*=-1;
        t.insert(temp);
    }
    for(set<term,cmp>::iterator itr=t.p.begin();itr!=t.p.end();itr++)res.insert(*itr);
    
    return res;
}

inline P operator *(const P &A,const P &B)
{
    P res;
    set<term,cmp>::iterator ita,itb;
    ita=A.p.begin();itb=B.p.begin();
    
    for(;ita!=A.p.end();ita++)for(itb=B.p.begin();itb!=B.p.end();itb++)res.insert((*ita)*(*itb));
    return res;
}

struct deal
{
    stack<char>S1;//oper
    stack<P>S2;//poly
    char str[N];
    int pre[300];
    int n;
    
    inline bool op(char c)
    {
        return (c=='+'||c=='-'||c=='*');
    }
    
    inline void calc()
    {
        char t=S1.top();S1.pop();
        P p1,p2,res;
        p2=S2.top();S2.pop();
        p1=S2.top();S2.pop();
        if(t=='+')res=p1+p2;
        else if(t=='-')res=p1-p2;
        else res=p1*p2;
        S2.push(res);
    }
    
    inline void work()
    {
        scanf("%s",str+1);n=strlen(str+1);
        pre['+']=pre['-']=1;pre['*']=2;
        rep(i,1,n)
        {
            if(str[i]=='[')str[i]='(';
            if(str[i]==']')str[i]=')';
        }
        rep(i,1,n)
        {
            if(op(str[i]))
            {
                while(!S1.empty()&&pre[S1.top()]>=pre[str[i]]&&S1.top()!='(')
                    calc();
                S1.push(str[i]);
            }else if(str[i]=='(')
            {
                S1.push(str[i]);
            }else if(str[i]==')')
            {
                while(!S1.empty()&&S1.top()!='(')calc();
                if(S1.top()=='(')S1.pop();
            }else
            {
                int j=0,sum=0;
                P poly;
                term res=term();
                for(;str[i+j]>='0'&&str[i+j]<='9';j++)sum=sum*10+str[i+j]-'0';
                for(;str[i+j]>='a'&&str[i+j]<='z';j++)
                {
                    if(str[i+j+1]=='^')
                    {
                        res.s[str[i+j]-'a'+1]=str[i+j+2]-'0';
                        j+=2;
                    }
                    else res.s[str[i+j]-'a'+1]=1;
                    
                }
                
                if(sum==0)sum=1;
                res.s[0]=sum;
                
                poly.insert(res); 
                S2.push(poly);
                i+=j-1; 
            }
        }
        while(!S1.empty())calc();
        
        set<term,cmp> res=S2.top().p;
        set<term,cmp>::iterator itr=res.begin();//*itr->term
        
        for(int i=0;itr!=res.end();itr++,i++)
        {
            if((*itr).s[0]==0)continue; 
            if((*itr).s[0]>0&&i!=0)printf("+");
            
            if((*itr).s[0]!=1)
            {
                if((*itr).s[0]==-1)printf("-");
                else printf("%d",(*itr).s[0]);
            }
            
            rep(j,1,26)if((*itr).s[j])
            {
                printf("%c",'a'+j-1);
                if((*itr).s[j]>1)printf("^%d",(*itr).s[j]);
            }
        }
    }
    
};
int main()
{
    deal D;
    D.work();
    return 0; 
}

 

以上~