ex05 汉诺塔1 递归解法

描述

传说，在世界中心贝拿勒斯（在印度北部）的圣庙外有左中右三根足够长的柱子
左边柱子上套着 64 片金片，金片按“上小下大”排，其余两根是空柱子
僧人们借助中间的柱子将左边柱子上的金片移动到右边……

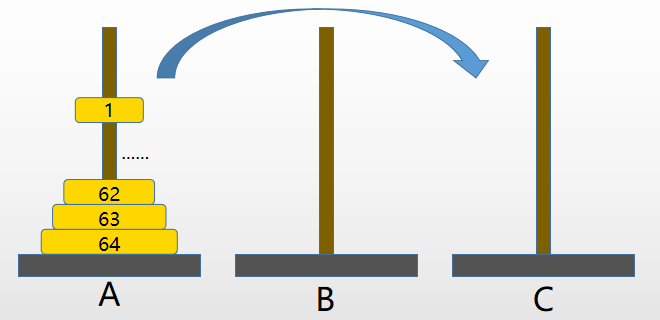
要求

• 一次只能移动一片
• 金片之间，必须是上小下大，即大金片不能放到小金片上
• 借助中间柱子，将左边柱子上所有的金片都移到右边柱子为止

程序

def hanoi(n, left, mid, right):
    if n == 1:
        print(left, '->', right)  # 将左塔的金片移到右塔
    else:
        hanoi(n - 1, left, right, mid)  # 将左塔的 n-1 层金片借助右塔移到中塔
        print(left, '->', right)  # 将左塔的最后一层金片移到右塔
        hanoi(n - 1, mid, left, right)  # 将中塔的 n-1 层金片借助左塔移到右塔


hanoi(64, 'A', 'B', 'C')  # 将 A 塔的 64 层金片借助 B 塔移到 C 塔

• 非递归解法详见下一篇：ex06 汉诺塔2 非递归解法