快速排序（改进的冒泡排序）

　　快速排序的基本思想：从记录中选定一个关键字，将待排序记录分割成两部分，其中一部分记录的关键字小于选定关键字的值，另一部分记录的关键字大于选定关键字的值；反复对分割好的记录进行上述操作，直到整个序列变为有序序列。

　　以顺序表L = {0，5，1，9，8，3}为例，length = 5，r[0]不参与排序。

　　快速排序的代码如下所示：

 1 //交换顺序表L中的记录，使枢轴记录放到正确位置，并返回其所在位置
 2 //交换结束后，枢轴记录前面的记录值小于枢轴记录的值
 3 //后面的记录值大于枢轴记录的值
 4 int Partition(SqList* L, int low, int high)
 5 {
 6     int pivotkey;
 7     pivotkey = L->r[low];//子表的第一个记录当作枢轴记录
 8 
 9     while (low < high)
10     {
11         //从右往左，找比枢轴记录关键字的值小的记录
12         while (low < high && L->r[high] >= pivotkey)
13             high--;
14         swap(L, low, high);//将比枢轴记录小的记录交换到低端
15 
16         //从左往右，找比枢轴记录关键字的值大的记录
17         while (low < high && L->r[low] <= pivotkey)
18             low++;
19         swap(L, low, high);//将比枢轴记录大的记录交换到高端
20     }
21 
22     return low;//返回枢轴所在的位置
23 }

 1 //对L->r[low,...,high]做快速排序
 2 void QSort(SqList* L, int low, int high)
 3 {
 4     int pivot;
 5     if (low < high)
 6     {
 7         pivot = Partition(L, low, high);//枢轴的位置
 8 
 9         QSort(L, low, pivot - 1);//对L->r[low,...,pivot - 1]递归排序
10         QSort(L, pivot + 1, high);//对L->r[pivot,...,high]递归排序
11     }
12 }

　　执行Partition函数后顺序表中的记录变化如下所示：

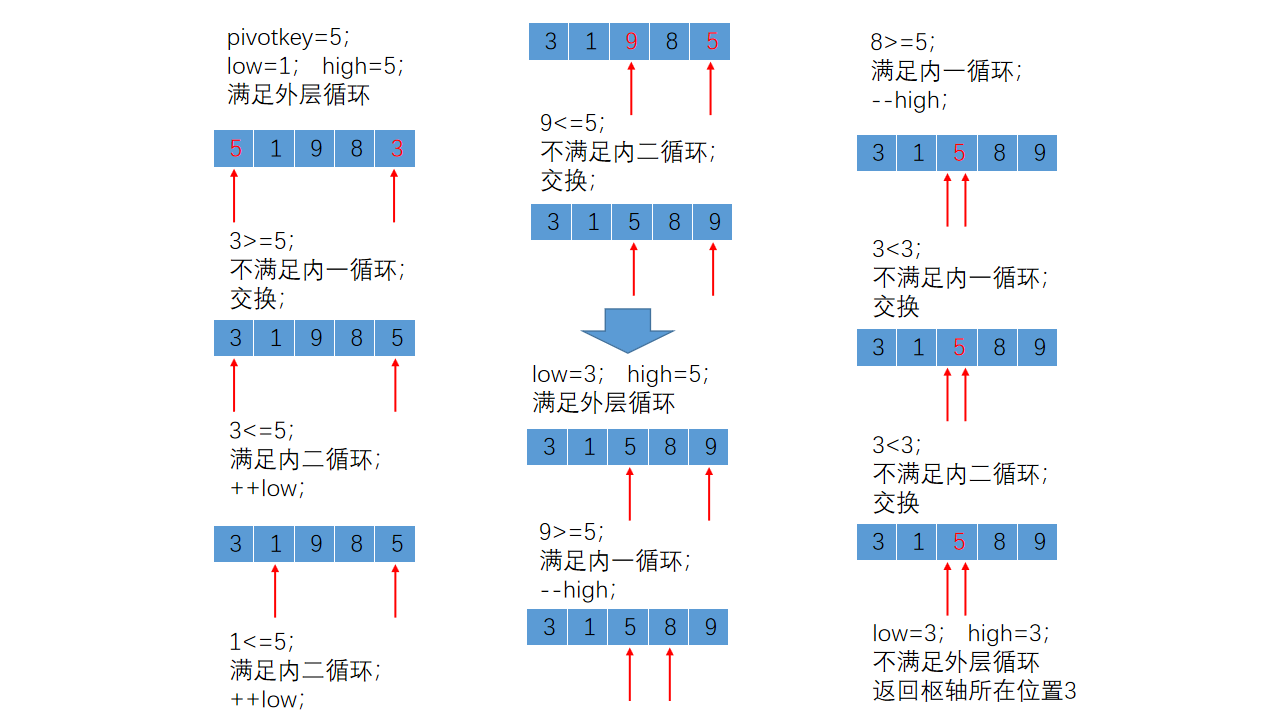
　　上述操作使枢轴记录5到位，并返回其所在位置3，接下来，对低子表{3，1}和高子表{8，9}进行同样的操作，最终将顺序表排序为有序表。

　　可以从一下几个方面对快速排序进行优化：

　　（1）优化枢轴的选取。枢轴记录的选择，其值居于待排序记录的中间最好，然而，将子表的第一个记录当作枢轴记录，并不能保证其关键字的值居于待排序记录的中间，所以衍生出了三数取中，九数取中等优化枢轴的选取的方法。我们选择三数取中法来对快速排序进行优化，即取待排序记录的左中右三个位置（也可以按其他方式取）的记录中关键字的值居中的记录作为枢轴记录。

　　（2）优化不必要的交换。如上所示，选定的数轴5的最终位置为3，而我们在将枢轴记录放到该正确的位置的过程中，不断地调整枢轴的位置，也就是不断地进行交换，这些交换都是不必要的，我么可以采用替换操作来代替交换操作，当找到枢轴的位置时，将枢轴值存入该位置。

　　（3）优化小数组的排序。当数组较小时，直接插入排序的性能更好，所以可以在代码中加入判断条件，当数组较小时，选用直接插入排序；当数组较大时，选用快速排序。

　　（4）优化递归操作。栈的大小是有限的，且每次递归调用都会占用一定的栈空间，函数的参数越多，占用的栈空间越大，所以可以通过减少递归来提高程序的性能。我们采用尾递归来减少递归次数。

　　优化的快速排序的代码如下所示：

 1 //交换顺序表L中的记录，使枢轴记录放到正确位置，并返回其所在位置
 2 //交换结束后，枢轴记录前面的记录值小于枢轴记录的值
 3 //后面的记录值大于枢轴记录的值
 4 int Partition(SqList* L, int low, int high)
 5 {
 6     int pivotkey;
 7 
 8     /********************************************************/
 9     //优化枢纽的选取
10     int mid = (low + high) / 2;
11     if (L->r[low] > L->r[high])
12         swap(L, low, high);
13     if (L->r[mid] > L->r[high])
14         swap(L, high, mid);
15     if (L->r[mid] > L->r[low])
16         swap(L, mid, low);
17     /********************************************************/
18 
19     pivotkey = L->r[low];
20 
21     /********************************************************/
22     //优化不必要的交换
23     L->r[0] = pivotkey;
24     /********************************************************/
25 
26     while (low < high)
27     {
28         while (low < high && L->r[high] >= pivotkey)
29             high--;
30 
31         /********************************************************/
32         //优化不必要的交换
33         L->r[low] = L->r[high];
34         /********************************************************/
35 
36         swap(L, low, high);
37         while (low < high && L->r[low] <= pivotkey)
38             low++;
39 
40         /********************************************************/
41         //优化不必要的交换
42         L -> r[high] = L->r[low];
43         /********************************************************/
44 
45         swap(L, low, high);
46     }
47 
48     /********************************************************/
49     //优化不必要的交换
50     L->r[low] = L->r[0];
51     /********************************************************/
52 
53     return low;
54 }

 1 //对L->r[low,...,high]做快速排序
 2 void QSort(SqList *L,int low,int high)
 3 {
 4     int pivot;
 5 
 6     /********************************************************/
 7     //优化递归操作
 8     while (low < high)
 9     /********************************************************/
10     {
11         pivot = Partition(L, low, high);//枢轴的位置
12 
13         QSort(L, low, pivot - 1);//对L->r[low,...,pivot - 1]递归排序
14 
15         /********************************************************/
16         //优化递归操作
17         low = pivot + 1;//尾递归
18         /********************************************************/
19     }
20 }

　　执行Partition函数后顺序表中的记录变化如下所示：

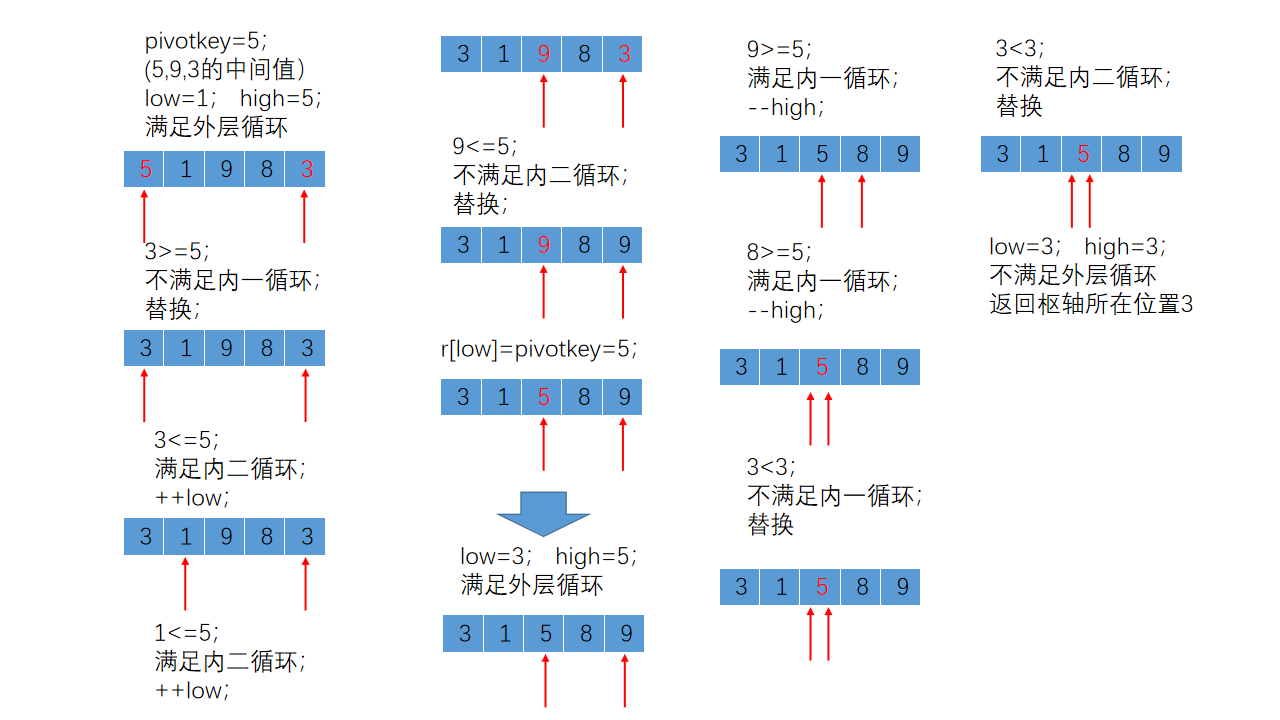
　　到此为止，我们介绍完了所有的排序算法，下一次会对所有的排序算法进行一个总结，对各种排序算法进行比较，分析其时间复杂度以及适用情况。接下来会依次介绍查找算法，希望给位同侪可以多多关注，给出指导意见，多多交流！

封狼居胥

快速排序（改进的冒泡排序）

公告