决策树系列（二）——剪枝

什么是剪枝？

      剪枝是指将一颗子树的子节点全部删掉，根节点作为叶子节点，以下图为例：

 

 

为甚么要剪枝？

      决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。

      考虑极端的情况，如果我们令所有的叶子节点都只含有一个数据点，那么我们能够保证所有的训练数据都能准确分类，但是很有可能得到高的预测误差，原因是将训练数据中所有的噪声数据都”准确划分”了，强化了噪声数据的作用。

      剪枝修剪分裂前后分类误差相差不大的子树，能够降低决策树的复杂度，降低过拟合出现的概率。

 

怎样剪枝？

两种方案：先剪枝和后剪枝

      先剪枝说白了就是提前结束决策树的增长，跟上述决策树停止生长的方法一样。

      后剪枝是指在决策树生长完成之后再进行剪枝的过程。这里介绍三种后剪枝方案：

（1）REP—错误率降低剪枝        

      顾名思义，该剪枝方法是根据错误率进行剪枝，如果一棵子树修剪前后错误率没有下降，就可以认为该子树是可以修剪的。

      REP剪枝需要用新的数据集，原因是如果用旧的数据集，不可能出现分裂后的错误率比分裂前错误率要高的情况。由于使用新的数据集没有参与决策树的构建，能够降低训练数据的影响，降低过拟合的程度，提高预测的准确率。

（2）PEP—悲观剪枝

      悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话，则进行剪枝。怎样才算是没有影响？如果剪枝后的误差小于剪枝前经度的上限，则说明剪枝后的效果与剪枝前的效果一致，此时要进行剪枝。

      进行剪枝必须满足的条件：

其中：

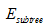    表示剪枝前子树的误差；

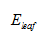   表示剪枝后节点的误差；

两者的计算公式如下：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

      令子树误差的经度满足二项分布，根据二项分布的性质， ， ，其中 ，N为子树的数据量；同样，叶子节点的误差。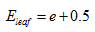

      上述公式中，0.5表示修正因子。由于子节点是父节点进行分裂的结果，从理论上讲，子节点的分类效果总比父节点好，分类的误差更小，如果单纯通过比较子节点和父节点的误差进行剪枝就完全没有意义了，因此对节点的误差计算方法进行修正。修正的方法是给每一个节点都加上误差修正因子0.5，在计算误差的时候，子节点由于加上了误差修正因子，就无法保证总误差低于父节点。

算例：

 

  

    

      由于 ，所以应该进行剪枝。

（3）CCP—代价复杂度剪枝

      代价复杂度选择节点表面误差率增益值最小的非叶子节点，删除该非叶子节点的左右子节点，若有多个非叶子节点的表面误差率增益值相同小，则选择非叶子节点中子节点数最多的非叶子节点进行剪枝。

可描述如下：

      令决策树的非叶子节点为。

      a） 计算所有非叶子节点的表面误差率增益值  

      b）选择表面误差率增益值最小的非叶子节点（若多个非叶子节点具有相同小的表面误差率增益值，选择节点数最多的非叶子节点）。

      c）对选中的非叶子节点进行剪枝

表面误差率增益值的计算公式：

 

其中：

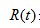表示叶子节点的误差代价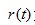， ， 为节点的错误率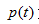， 为节点数据量的占比；

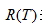表示子树的误差代价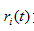，， 为子节点i的错误率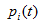，  表示节点i的数据节点占比；

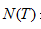表示子树节点个数。

算例：

下图是决策树A的其中一颗子树，决策树的总数据量为40。

 

该子树的表面误差率增益值可以计算如下：

 

求出该子树的表面错误覆盖率为 1/40，只要求出其他子树的表面误差率增益值就可以对决策树进行剪枝.