【Java】 大话数据结构(17) 排序算法(4) （归并排序）

　　本文根据《大话数据结构》一书，实现了Java版的归并排序。

更多：数据结构与算法合集

基本概念

　　归并排序：将n个记录的序列看出n个有序的子序列，每个子序列长度为1，然后不断两两排序归并，直到得到长度为n的有序序列为止。

　　归并方法：每次在两个子序列中找到较小的那一个赋值给合并序列（通过指针进行操作）。当一个子序列遍历完成后，将另一个序列中剩下数赋值给合并序列。（详见代码）

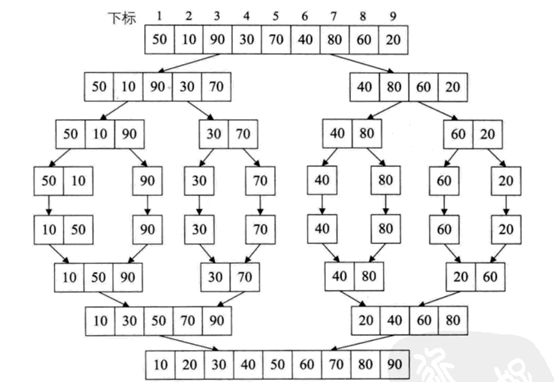
归并排序示意图

 

完整Java代码

（含测试代码）

public class MergeSort {
    public void mergeSort(int[] arr) {
        if(arr==null || arr.length<=0)
            return;
        mSort(arr,0,arr.length-1);
    }
 
    private  void mSort(int[] arr, int start, int end) {
        if(start==end)
            return;
        int mid=(start+end)/2;
        mSort(arr,start,mid);
        mSort(arr, mid+1, end);
        merge(arr,start,mid,end);
    }
 
    private void merge(int[] arr, int start, int mid, int end) {
        int[] temp=new int[end-start+1];    //存放排序号数据的临时区域
        int k=0;        //临时区域的指针
        int i=start;    //第一个有序区的指针
        int j=mid+1;    //第二个有序区的指针
         
        while(i<=mid && j<=end) {
            if(arr[i]<=arr[j])
                temp[k++]=arr[i++];
            else
                temp[k++]=arr[j++];
        }
        while(i<=mid)
            temp[k++]=arr[i++];
        while(j<=end)
            temp[k++]=arr[j++];
         
        for(k=0;k<=end-start;k++)
            arr[k+start]=temp[k];
    }
     
    //==========测试代码=================
    public void test1() {
        int[] a = null;
        mergeSort(a);
        System.out.println(Arrays.toString(a));
    }
 
    public void test2() {
        int[] a = {};
        mergeSort(a);
        System.out.println(Arrays.toString(a));
    }
 
    public void test3() {
        int[] a = { 1 };
        mergeSort(a);
        System.out.println(Arrays.toString(a));
    }
 
    public void test4() {
        int[] a = { 3, 3, 3, 3, 3 };
        mergeSort(a);
        System.out.println(Arrays.toString(a));
    }
 
    public void test5() {
        int[] a = { -3, 6, 3, 1, 3, 7, 5, 6, 2 };
        mergeSort(a);
        System.out.println(Arrays.toString(a));
    }
    public static void main(String[] args) {
        MergeSort demo =new MergeSort();
        demo.test1();
        demo.test2();
        demo.test3();
        demo.test4();
        demo.test5();
    }
}

　　

null
[]
[1]
[3, 3, 3, 3, 3]
[-3, 1, 2, 3, 3, 5, 6, 6, 7]

 

复杂度

 　　时间复杂度：O(nlogn)。假设序列有n个数，遍历一次时间复杂度为O(n)，遍历次数为二叉树的深度log(2)n，所以时间复杂度为O(nlogn)。

　　归并排序是一种比较占用内存，但效率高且稳定的算法。

 

更多：数据结构与算法合集