【Java】 大话数据结构(16) 排序算法(3) （堆排序）

本文根据《大话数据结构》一书，实现了Java版的堆排序。

更多：数据结构与算法合集

基本概念

　　堆排序种的堆指的是数据结构中的堆，而不是内存模型中的堆。

　　堆：可以看成一棵完全二叉树，每个结点的值都大于等于（小于等于）其左右孩子结点的值，称为大顶堆（小顶堆）。

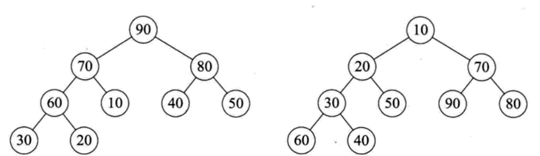
大顶堆(左)与小顶堆(右)

　　堆排序的基本思想：将带排序的序列构造成大顶堆，最大值为根结点。将根结点与最后一个元素交换，对除最大值外的剩下n-1个元素重新构造成大顶堆，可以获得次大的元素。反复执行，就可以得到一个有序序列了。

　　构造大顶堆的方法：

　　1.首先复习完全二叉树的性质，层序遍历，当第一个元素索引从0开始时，索引为i的左孩子的索引是 (2*i+1)，右孩子的索引是 (2*i+2)。

　　2.设计一个函数heapAdjust()，对于一个序列（除了第一个根结点外，其余结点均满足最大堆的定义），通过这个函数可以将序列调整为正确的大顶堆。

　　3.正式构造：将带排序的序列看成一棵完全二叉树的层序遍历，我们从下往上，从右往左，依次将每个非叶子结点当作根结点，使用heapAdjust()调整成大顶堆。

　　具体细节的实现参阅代码，比较清楚，不再赘述。

完整Java代码

（含测试代码）

/**
 * 
 * @Description 堆排序
 *
 * @author yongh
 * 
 */
public class HeapSort {
	public void heapSort(int[] arr) {
		if(arr==null || arr.length<=0)
			return;
		int len=arr.length;
		for(int i=len/2-1;i>=0;i--) { //从最后一个父结点开始构建最大堆
			heapAdjust(arr,i,len-1);
		}
		for(int i=len-1;i>=0;i--) {
			int temp=arr[0];
			arr[0]=arr[i];
			arr[i]=temp;
			heapAdjust(arr, 0, i-1);
		}
	}
	
	
	/*
	 * 功能：调整堆为最大堆
	 * [i……j]中，除了i之外，部分子树都满足最大堆定义
	 */
	private void heapAdjust(int[] arr, int start, int end) {
		int temp=arr[start];
		int child=2*start+1;
		while(child<=end) {
			if(child+1<=end && arr[child+1]>arr[child])  //记得child+1<=end的判断
				child++;  //较大的孩子
			if(arr[child]<=temp) 
				break;
			arr[start]=arr[child];
			start=child;
			child=child*2+1;
		}
		arr[start]=temp;	
		}
	
	// =========测试代码=======
	public void test1() {
		int[] a = null;
		heapSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test2() {
		int[] a = {};
		heapSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test3() {
		int[] a = { 1 };
		heapSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test4() {
		int[] a = { 3, 3, 3, 3, 3 };
		heapSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test5() {
		int[] a = { -3, 6, 3, 1, 3, 7, 5, 6, 2 };
		heapSort(a);
		System.out.println(Arrays.toString(a));
	}

	public static void main(String[] args) {
		HeapSort demo = new HeapSort();
		demo.test1();
		demo.test2();
		demo.test3();
		demo.test4();
		demo.test5();
	}
}
	
	

　　

null
[]
[1]
[3, 3, 3, 3, 3]
[-3, 1, 2, 3, 3, 5, 6, 6, 7]

 

复杂度分析

 　　构建堆的时间复杂度为O(n)；每次调整堆的时间为O(logn)，共要调整n-1次，所以重建堆的时间复杂度为O(nlogn)。

　　因此总体来说，堆排序的复杂度为O(nlogn)。不过由于记录的比较和交换是跳跃式进行的，因此堆排序是不稳定的排序方法。

 

更多：数据结构与算法合集