【Java】 大话数据结构(15) 排序算法(2) (快速排序及其优化)
本文根据《大话数据结构》一书,实现了Java版的快速排序。
更多:数据结构与算法合集
基本概念
基本思想:在每轮排序中,选取一个基准元素,其他元素中比基准元素小的排到数列的一边,大的排到数列的另一边;之后对两边的数列继续进行这种排序,最终达到整体有序。
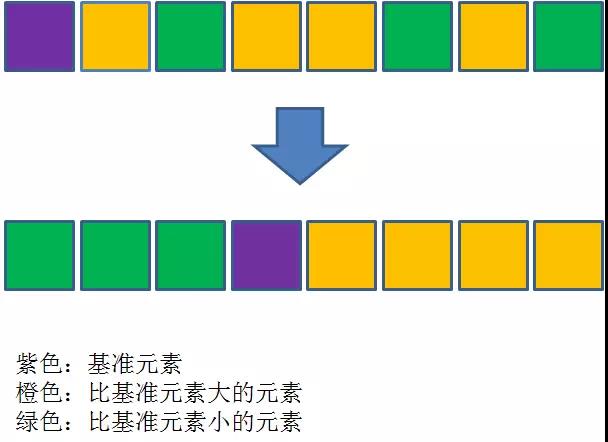
图片来自公众号:程序员小灰
实现代码
根据上述基本思想,可以先写出快速排序最核心的代码:对于数组a中从下标为low至下标为high的元素,选取一个基准元素(记为pivotKey),根据与基准比较的大小,将这些元素排到基准元素的两端。
注意点:1.两端向中间扫描时,一定要先从高段往低端扫描(low<high && a[high]<pivotKey),这样才能实现pivotKey一直会交换到中间。!!
2.比较大小时不要忘记low<high还要一直成立,即(low<high && a[high]<pivotKey)。!! 例如,数组全为同一个数字时,不加这个判断有可能导致越界
/**
* 对数组a中下标从low到high的元素,选取基准元素pivotKey,
* 根据与基准比较的大小,将各个元素排到基准元素的两端。
* 返回值为最后基准元素的位置
*/
public int partition(int[] a, int low, int high) {
int pivotKey = a[low]; //用第一个元素作为基准元素
while (low < high) { //两侧交替向中间扫描
while (low < high && a[high] >= pivotKey)
high--;
swap(a, low, high); //比基准小的元素放到低端
while (low < high && a[low] <= pivotKey)
low++;
swap(a, low, high); //比基准大的元素放到高端
}
return low; //返回基准元素所在位置
}
将元素分为两部分后,必须对两个子部分继续进行上面的排序,所以要用到递归。代码如下:
/**
* 递归调用
*/
public void qSort(int[] a, int low, int high) {
int pivot;
if (low >= high)
return;
pivot = partition(a, low, high); //将数列一分为二
qSort(a, low, pivot - 1); //对低子表排序
qSort(a, pivot + 1, high); //对高子表排序
}
完整Java代码
(含测试代码)
import java.util.Arrays;
/**
*
* @Description 快速排序
*
* @author yongh
* @date 2018年9月14日 下午2:39:00
*/
public class QuickSort {
public void quickSort(int[] a) {
if (a == null)
return;
qSort(a, 0, a.length - 1);
}
/**
* 递归调用
*/
public void qSort(int[] a, int low, int high) {
int pivot;
if (low >= high)
return;
pivot = partition(a, low, high); //将数列一分为二
qSort(a, low, pivot - 1); //对低子表排序
qSort(a, pivot + 1, high); //对高子表排序
}
/**
* 对数组a中下标从low到high的元素,选取基准元素pivotKey,
* 根据与基准比较的大小,将各个元素排到基准元素的两端。
* 返回值为最后基准元素的位置
*/
public int partition(int[] a, int low, int high) {
int pivotKey = a[low]; //用第一个元素作为基准元素
while (low < high) { //两侧交替向中间扫描
while (low < high && a[high] >= pivotKey)
high--;
swap(a, low, high); //比基准小的元素放到低端
while (low < high && a[low] <= pivotKey)
low++;
swap(a, low, high); //比基准大的元素放到高端
}
return low; //返回基准元素所在位置
}
public void swap(int[] a, int i, int j) {
int temp;
temp = a[j];
a[j] = a[i];
a[i] = temp;
}
// =========测试代码=======
public void test1() {
int[] a = null;
quickSort(a);
System.out.println(Arrays.toString(a));
}
public void test2() {
int[] a = {};
quickSort(a);
System.out.println(Arrays.toString(a));
}
public void test3() {
int[] a = { 1 };
quickSort(a);
System.out.println(Arrays.toString(a));
}
public void test4() {
int[] a = { 3, 3, 3, 3, 3 };
quickSort(a);
System.out.println(Arrays.toString(a));
}
public void test5() {
int[] a = { -3, 6, 3, 1, 3, 7, 5, 6, 2 };
quickSort(a);
System.out.println(Arrays.toString(a));
}
public static void main(String[] args) {
QuickSort demo = new QuickSort();
demo.test1();
demo.test2();
demo.test3();
demo.test4();
demo.test5();
}
}

null [] [1] [3, 3, 3, 3, 3] [-3, 1, 2, 3, 3, 5, 6, 6, 7]
快速排序优化
1.优化选取枢纽
基准应尽量处于序列中间位置,可以采取“三数取中”的方法,在partition()方法开头加以下代码,使得a[low]为三数的中间值:
// 三数取中,将中间元素放在第一个位置 if (a[low] > a[high]) swap(a, low, high); if (a[(low + high) / 2] > a[high]) swap(a, (low + high) / 2, high); if (a[low] < a[(low + high) / 2]) swap(a, (low + high) / 2, low);
2.优化不必要的交换
两侧向中间扫描时,可以将交换数据变为替换:
while (low < high) { // 两侧交替向中间扫描
while (low < high && a[high] >= pivotKey)
high--;
a[low] = a[high];
// swap(a, low, high); //比基准小的元素放到低端
while (low < high && a[low] <= pivotKey)
low++;
a[high] = a[low];
// swap(a, low, high); //比基准大的元素放到高端
}
a[low]=pivotKey; //在中间位置放回基准值
3.优化小数组时的排序方案
当数组非常小时,采用直接插入排序(简单排序中性能最好的方法)
4.优化递归操作
qSort()方法中,有两次递归操作,递归对性能有较大影响。因此,使用while循环,在第一次递归后,变量low就没有用处了,可将pivot+1赋值给low,下次循环中,partition(a, low, high)的效果等同于qSort(a, pivot + 1, high),从而可以减小堆栈的深度,提高性能。
// pivot = partition(a, low, high); // 将数列一分为二
// qSort(a, low, pivot - 1); // 对低子表排序
// qSort(a, pivot + 1, high); // 对高子表排序
//优化递归操作
while (low < high) {
pivot = partition(a, low, high); // 将数列一分为二
qSort(a, low, pivot - 1); // 对低子表排序
low = pivot + 1;
}
复杂度分析
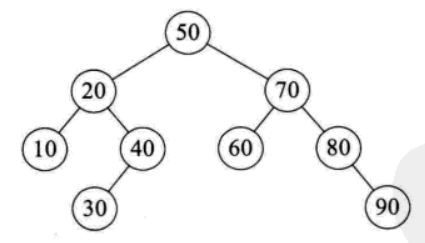
快速排序时间性能取决于递归深度,而空间复杂度是由递归造成的栈空间的使用。递归的深度可以用递归树来描述,如{50,10,90,30,70,40,80,60,20}的递归树如下:
最优情况:
最优情况下,每次选取的基准元素都是元素中间值,partition()方法划分均匀,此时根据二叉树的性质4可以知道,排序n个元素,其递归树的深度为[log2n]+1,所以仅需要递归log2n次。
将排序n个元素的时间记为T(n),则有以下推断:
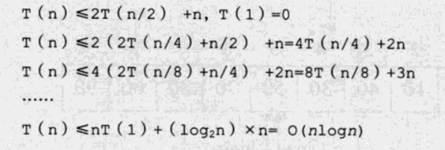
所以最优情况下的时间复杂度为:O(nlogn);同样根据递归树的深度,最优空间复杂度为O(logn)。
最坏情况:
递归树为一棵斜树,需要n-1次调用,所以最坏空间复杂度为O(logn)。在第i次调用中需要n-1次的关键字比较,所以比较次数为:Σ(n-i)=(n-1)+……+2+1=n(n-1)/2,所以最坏时间复杂度为O(n^2)。
平均情况:

平均时间复杂度:O(nlogn),平均空间复杂度O(logn)。
更多:数据结构与算法合集




 浙公网安备 33010602011771号
浙公网安备 33010602011771号