【Java】 大话数据结构(14) 排序算法(1) (冒泡排序及其优化)
本文根据《大话数据结构》一书,实现了Java版的冒泡排序。
更多:数据结构与算法合集
基本概念
基本思想:将相邻的元素两两比较,根据大小关系交换位置,直到完成排序。
对n个数组成的无序数列,进行n轮排序,每轮按两两比较的方法找出最小(或最大)的一个。下图表示某数列的第一轮排序。

下面为交换元素的swap()方法代码,后面代码中将直接使用。
public void swap(int[] a, int i, int j) {
int temp;
temp = a[j];
a[j] = a[i];
a[i] = temp;
}
初级版本
根据基本思想,可以写出初级版本的冒泡排序如下:
public void bubbleSort0(int[] a) {
if(a==null) return;
// 代表第i轮排序
for (int i = 0; i < a.length; i++) {
for (int j = a.length - 1; j > i; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
}
}
}
}
第一次优化版本
当数据基本有序时,可能前几轮循环就完成了排序,后面的循环就没有必要继续进行了,如下图所示:
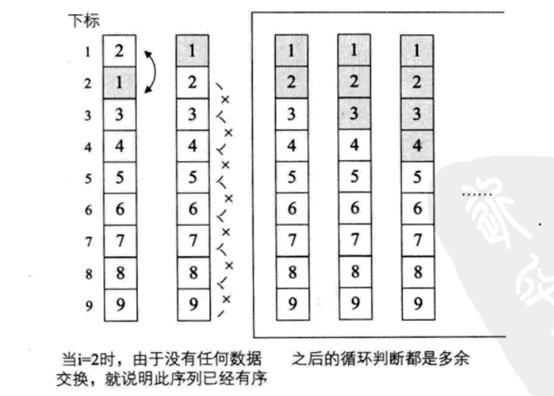
对这种情况,可以在代码中增加一个标记,用于标记每轮循环时代码是否已经有序,在每轮循环开始前,如果有序的话就没有必要继续进行比较了。具体Java代码如下:
public void bubbleSort1(int[] a) {
if(a==null) return;
boolean isSorted = false; // false代表数据无序,需要排序
for (int i = 0; i < a.length && !isSorted; i++) { // 数据无序时还要继续循环
isSorted = true; // 假设这轮循环开始时已经有序
for (int j = a.length - 1; j > i; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
isSorted = false; // 有发生交换,说明这轮循环还是无序的
}
}
}
}
第二次优化版本
当数列的前半部分有序而后半部分无序时,每轮循环没必要再对有序部分进行排序,例如,数列为{1,2,3,4,9,5,8,7}时,在一次循环后知道1,2,3,4已经有序,后面的循环就没必要对这些数字进行排序了。
此时,关键点在于对有序区的界定:如果知道有序区的边界,那么每次循环就只需要比较到该边界即可。在每次循环的最后,记录下最后一次元素交换的位置,该位置就是有序区的边界了。具体Java代码如下:
public void bubbleSort2(int[] a) {
if(a==null) return;
int lastExchangeIndex = 0; // 用于记录每轮循环最后一次交换的位置
int sortBorder = 0; // 有序数组的边界,每次比较只要比较到这里就可以
boolean isSorted = false;
for (int i = 0; i < a.length && !isSorted; i++) {
isSorted = true;
for (int j = a.length - 1; j > sortBorder; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
isSorted = false;
lastExchangeIndex = j; // 本轮最后一次交换位置(不断更新)
}
}
sortBorder = lastExchangeIndex; // 边界更新为最后一次交换位置
}
}
完整Java代码
(含测试代码)
import java.util.Arrays;
/**
*
* @Description 冒泡排序(从小到大)
*
* @author yongh
* @date 2018年9月13日 下午3:21:38
*/
public class BubbleSort {
/**
* 初级版本
*/
public void bubbleSort0(int[] a) {
if(a==null) return;
// 代表第i轮排序
for (int i = 0; i < a.length; i++) {
for (int j = a.length - 1; j > i; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
}
}
}
}
/**
* 优化版本
* 添加一个标记isSorted
*/
public void bubbleSort1(int[] a) {
if(a==null) return;
boolean isSorted = false; // false代表数据无序,需要排序
for (int i = 0; i < a.length && !isSorted; i++) { // 数据无序时还要继续循环
isSorted = true; // 假设这轮循环开始时已经有序
for (int j = a.length - 1; j > i; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
isSorted = false; // 有发生交换,说明这轮循环还是无序的
}
}
}
}
/**
* 进一步优化版本
*/
public void bubbleSort2(int[] a) {
if(a==null) return;
int lastExchangeIndex = 0; // 用于记录每轮循环最后一次交换的位置
int sortBorder = 0; // 有序数组的边界,每次比较只要比较到这里就可以
boolean isSorted = false;
for (int i = 0; i < a.length && !isSorted; i++) {
isSorted = true;
for (int j = a.length - 1; j > sortBorder; j--) {
if (a[j] < a[j - 1]) {
swap(a, i, j);
isSorted = false;
lastExchangeIndex = j; // 本轮最后一次交换位置(不断更新)
}
}
sortBorder = lastExchangeIndex; // 边界更新为最后一次交换位置
}
}
/**
* 交换代码
*/
public void swap(int[] a, int i, int j) {
int temp;
temp = a[j];
a[j] = a[i];
a[i] = temp;
}
//=========测试代码=======
public void test1() {
int[] a = null;
bubbleSort2(a);
System.out.println(Arrays.toString(a));
}
public void test2() {
int[] a = {};
bubbleSort2(a);
System.out.println(Arrays.toString(a));
}
public void test3() {
int[] a = { 1 };
bubbleSort2(a);
System.out.println(Arrays.toString(a));
}
public void test4() {
int[] a = { 3, 3, 3, 3, 3 };
bubbleSort2(a);
System.out.println(Arrays.toString(a));
}
public void test5() {
int[] a = { -3, 6, 3, 1, 3, 7, 5, 6, 2 };
bubbleSort2(a);
System.out.println(Arrays.toString(a));
}
public static void main(String[] args) {;
BubbleSort demo = new BubbleSort();
demo.test1();
demo.test2();
demo.test3();
demo.test4();
demo.test5();
}
}

null [] [1] [3, 3, 3, 3, 3] [3, 3, -3, 5, 2, 7, 1, 6, 6]
总结
冒泡排序原理近似于气泡在水里慢慢上浮到水面上,实现容易,但也有改进的空间,
改进1:若前几轮已经有序,则后面就没必要继续比较了,因此增加一个isSorted标记,对每轮是否有序进行标记。
改进2:一部分有序,则没必要继续对有序区比较,增加一个sortBorder来定义有序区边界,每次比较到该边界即可。该边界由每轮循环中最后一次元素交换的位置得到。
时间复杂度:O(n^2)
更多:数据结构与算法合集




 浙公网安备 33010602011771号
浙公网安备 33010602011771号