【Java】 大话数据结构(13) 查找算法(4) （散列表（哈希表））
本文根据《大话数据结构》一书，实现了Java版的一个简单的散列表（哈希表）。
基本概念
对关键字key，将其值存放在f(key)的存储位置上。由此，在查找时不需比较，只需计算出f(key)便可直接取得所查记录。这个函数 f() 就叫做散列函数，按这个思想建立的表称为散列表。
散列技术即是一种存储方法，又是一种查找方法：
存储过程：根据关键字key，算出f(key)，将记录存放在f(key)的位置上；
查找过程：根据关键字key，算出f(key)，该位置上的值即为要找的记录。
散列函数的构造方法
直接定址法
直接取关键字的线性函数为散列地址：f(key)=a×key+b（a，b为常数）
如：对下表的记录，关键字key取为出生年份，令f(key)=key-1980即可。
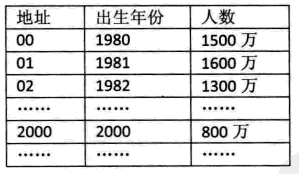
数字分析法
分析一组数据，找出其规律，尽可能利用这些数据来构造冲突几率较低的散列地址
如：以员工的手机号码作为关键字，前7位数字基本相同，可以选择后面四位数字作为散列地址。
平方取中法
当无法确定关键字中哪几位分布较均匀时，可以先求出关键字的平方值，然后按需要取平方值的中间几位作为散列地址。
折叠法
将关键字分割成位数相同的几部分，最后一部分位数可以不同，然后取这几部分的叠加和（去除进位）作为散列地址。
除留余数法
最为常用的方法，取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。
f(key) = key MOD p,p<=m。
随机数法
选择一随机函数（伪随机），取关键字的随机值作为散列地址，通常用于关键字长度不同的场合。
处理散列冲突的方法
当两个关键字key1和key2不同时，有f(key1)=f(key2)，这种现象称为冲突。一般情况下，我们会尽量设计恰当的散列函数减少冲突，但无法完全避免，这就需要对冲突进行处理。
开放寻址法
一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。根据下一个位置的不同，又可分为以下三种：
①线性探测法：
②二次探测法
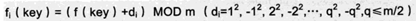
③随机探测法
再散列函数法
在同义词产生地址冲突时计算另一个散列函数地址，直到冲突不再发生，这种方法不易产生“聚集”，但增加了计算时间。如下图所示（RHi代表不同的散列函数）：
链地址法
相同地址的记录存放在一个单链表中，散列表值存储所有同义词子表的头指针。如下图所示：
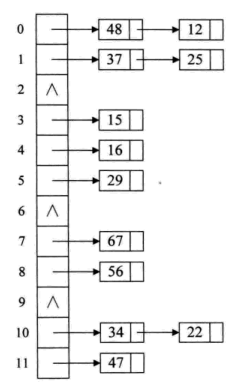
公共溢出区法
为所有冲突的关键字建立一个公共的溢出区来存放。
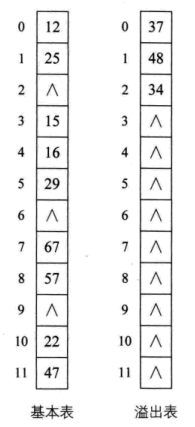
代码实现
接下来建立一个简单的散列表，其散列函数采用上述的除留余数法，处理冲突的方法采用开放定址法下的线性探测法。
Java代码如下：
package HashTable;
/**
* 散列表
* @author Yongh
*
*/
public class HashTable {
int[] elem;
int count;
private static final int Nullkey = -32768;
public HashTable(int count) {
this.count = count;
elem = new int[count];
for (int i = 0; i < count; i++) {
elem[i] = Nullkey; // 代表位置为空
}
}
/*
* 散列函数
*/
public int hash(int key) {
return key % count; // 除留余数法
}
/*
* 插入操作
*/
public void insert(int key) {
int addr = hash(key); // 求散列地址
while (elem[addr] != Nullkey) { // 位置非空，有冲突
addr = (addr + 1) % count; // 开放地址法的线性探测
}
elem[addr] = key;
}
/*
* 查找操作
*/
public boolean search(int key) {
int addr = hash(key); // 求散列地址
while (elem[addr] != key) {
addr = (addr + 1) % count; // 开放地址法的线性探测
if (addr == hash(key) || elem[addr] == Nullkey) { // 循环回到原点或者到了空地址
System.out.println("要查找的记录不存在！");
return false;
}
}
System.out.println("存在记录:" + key + ",位置为：" + addr);
return true;
}
public static void main(String[] args) {
int[] arr = { 12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34 };
HashTable aTable = new HashTable(arr.length);
for (int a : arr) {
aTable.insert(a);
}
for (int a : arr) {
aTable.search(a);
}
}
}
存在记录:12,位置为：0 存在记录:67,位置为：7 存在记录:56,位置为：8 存在记录:16,位置为：4 存在记录:25,位置为：1 存在记录:37,位置为：2 存在记录:22,位置为：10 存在记录:29,位置为：5 存在记录:15,位置为：3 存在记录:47,位置为：11 存在记录:48,位置为：6 存在记录:34,位置为：9
代码中重点可以看：插入操作是如何处理冲突 以及查找操作是如何判断记录是否存在的。
