【Java】 大话数据结构(11) 查找算法(2)（二叉排序树/二叉搜索树）

 

本文根据《大话数据结构》一书，实现了Java版的二叉排序树/二叉搜索树。

二叉排序树介绍

在上篇博客中，顺序表的插入和删除效率还可以，但查找效率很低；而有序线性表中，可以使用折半、插值、斐波那契等查找方法来实现，但因为要保持有序，其插入和删除操作很耗费时间。

二叉排序树(Binary Sort Tree)，又称为二叉搜索树，则可以在高效率的查找下，同时保持插入和删除操作也又较高的效率。下图为典型的二叉排序树。

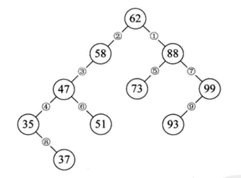
二叉查找树具有以下性质：

　　(1) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

　　(2) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

　　(3) 任意节点的左、右子树也分别为二叉查找树。

 

查找操作

思路：查找值与结点数据对比，根据大小确定往左子树还是右子树进行下一步比较。

采用递归的查找算法

	/*
	 * 查找
	 */
	public boolean SearchBST(int key) {
		return SearchBST(key, root);
	}

	private boolean SearchBST(int key, Node node) {
		if (node == null)
			return false;
		if (node.data == key) {
			return true;
		} else if (node.data < key) {
			return SearchBST(key, node.rChild);
		} else {
			return SearchBST(key, node.lChild);
		}
	}

　

采用非递归的查找算法

	/*
	 * 查找，非递归
	 */
	public boolean SearchBST2(int key) {
		Node p = root;
		while (p != null) {
			if (p.data > key) {
				p = p.lChild;
			} else if (p.data < key) {
				p = p.rChild;
			} else {
				return true;
			}
		}
		return false;
	}

　　

插入操作

思路：与查找类似，但需要一个父节点来进行赋值。

采用非递归的插入算法：

	/*
	 * 插入，自己想的，非递归
	 */
	public boolean InsertBST(int key) {
		Node newNode = new Node(key);
		if (root == null) {
			root = newNode;
			return true;
		}
		Node f = null; // 指向父结点
		Node p = root; // 当前结点的指针
		while (p != null) {
			if (p.data > key) {
				f = p;
				p = p.lChild;
			} else if (p.data < key) {
				f = p;
				p = p.rChild;
			} else {
				System.out.println("树中已有相同数据，不再插入！");
				return false;
			}
		}
		if (f.data > key) {
			f.lChild = newNode;
		} else if (f.data < key) {
			f.rChild = newNode;
		}
		return true;
	}

　　

采用递归的插入算法：

	/*
	 * 插入，参考别人博客，递归
	 * 思路：把null情况排除后用递归，否则无法赋值
	 */
	public boolean InsertBST2(int key) {
		if (root == null) {
			root = new Node(key);
			return true;
		}
		return InsertBST2(key, root);
	}

	private boolean InsertBST2(int key, Node node) {
		if (node.data > key) {
			if (node.lChild == null) {
				node.lChild = new Node(key);
				return true;
			} else {
				return InsertBST2(key, node.lChild);
			}
		} else if (node.data < key) {
			if (node.rChild == null) {
				node.rChild = new Node(key);
				return true;
			} else {
				return InsertBST2(key, node.rChild);
			}
		} else {
			System.out.println("树中已有相同数据，不再插入！");
			return false;
		}
	}

 

新补充：在写【Java】 大话数据结构(12) 查找算法(3) （平衡二叉树（AVL树））这篇博客时，发现以下的插入方法比较好（如果没有要求返回值必须为boolean格式的话）：（推荐使用此类方法）

	/*
	 * 插入操作
	 */
	public void insert(int key) {
		root = insert(root, key);
	}

	private Node insert(Node node, int key) {
		if (node == null) {
			// System.out.println("插入成功！");
			// 也可以定义一个布尔变量来保存插入成功与否
			return new Node(key);
		}
		if (key == node.data) {
			System.out.println("数据重复，无法插入！");
		} else if (key < node.data) {
			node.lChild=insert(node.lChild, key);
		} else {
			node.rChild=insert(node.rChild, key);
		}
		return node;
	}

　　

 

删除操作

思路：

（1）删除叶子结点

　　直接删除；

（2）删除仅有左或右子树的结点

　　子树移动到删除结点的位置即可；

（3）删除左右子树都有的结点

 　　找到删除结点p的直接前驱（或直接后驱）s，用s来替换结点p，然后删除结点s，如下图所示。

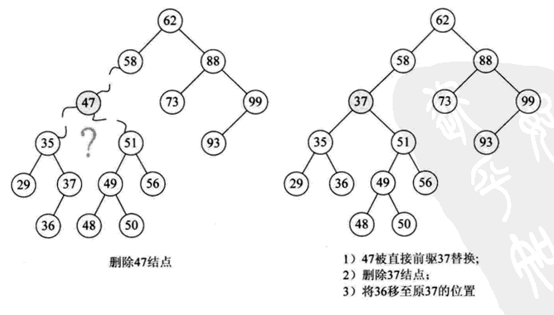
首先找到删除结点位置及其父结点

	/*
	 * 删除操作，先找到删除结点位置及其父结点
	 * 因为需要有父结点，所以暂时没想到递归的方法（除了令Node对象带个parent属性）
	 */
	public boolean deleteBST(int key) {
		if (root == null) {
			System.out.println("空表，删除失败");
			return false;
		}
		Node f = null; // 指向父结点
		Node p = root; // 指向当前结点
		while (p != null) {
			if (p.data > key) {
				f = p;
				p = p.lChild;
			} else if (p.data < key) {
				f = p;
				p = p.rChild;
			} else {
				delete(p, f);
				return true;
			}
		}
		System.out.println("该数据不存在");
		return false;
	}

　　

再根据上述思路进行结点p的删除：（需注意删除结点为根节点的情况）

	/*
	 * 删除结点P的操作
	 * 必须要有父结点,因为Java无法直接取得变量p的地址（无法使用*p=(*p)->lChild）
	 */
	private void delete(Node p, Node f) {// p为删除结点，f为其父结点
		if (p.lChild == null) { // 左子树为空，重接右子树
			if (p == root) { // 被删除结点为根结点时，无法利用f，该情况不能忽略
				root = root.rChild;
				p = null;
			} else {
				if (f.data > p.data) { // 被删结点为父结点的左结点，下同
					f.lChild = p.rChild;
					p = null; // 释放结点别忘了
				} else {// 被删结点为父结点的右结点，下同
					f.rChild = p.rChild;
					p = null;
				}
			}
		} else if (p.rChild == null) { // 右子树为空，重接左子树
			if (p == root) { // 被删除结点为根结点
				root = root.lChild;
				p = null;
			} else {
				if (f.data > p.data) {
					f.lChild = p.lChild;
					p = null;
				} else {
					f.rChild = p.lChild;
					p = null;
				}
			}
		} else { // 左右子树都不为空,删除位置用前驱结点替代
			Node q, s;
			q = p;
			s = p.lChild;
			while (s.rChild != null) { // 找到待删结点的最大前驱s
				q = s;
				s = s.rChild;
			}
			p.data = s.data; // 改变p的data就OK
			if (q != p) {
				q.rChild = s.lChild;
			} else {
				q.lChild = s.lChild;
			}
			s = null;
		}
	}

　　

　　

 

完整代码（含测试代码）

package BST;

/**
 * 二叉排序树（二叉查找树）
 * 若是泛型，则要求满足T extends Comparable<T> static问题
 * @author Yongh
 *
 */
class Node {
	int data;
	Node lChild, rChild;

	public Node(int data) {
		this.data = data;
		lChild = null;
		rChild = null;
	}
}

public class BSTree {
	private Node root;

	public BSTree() {
		root = null;
	}

	/*
	 * 查找
	 */
	public boolean SearchBST(int key) {
		return SearchBST(key, root);
	}

	private boolean SearchBST(int key, Node node) {
		if (node == null)
			return false;
		if (node.data == key) {
			return true;
		} else if (node.data < key) {
			return SearchBST(key, node.rChild);
		} else {
			return SearchBST(key, node.lChild);
		}
	}

	/*
	 * 查找，非递归
	 */
	public boolean SearchBST2(int key) {
		Node p = root;
		while (p != null) {
			if (p.data > key) {
				p = p.lChild;
			} else if (p.data < key) {
				p = p.rChild;
			} else {
				return true;
			}
		}
		return false;
	}

	/*
	 * 插入，自己想的，非递归
	 */
	public boolean InsertBST(int key) {
		Node newNode = new Node(key);
		if (root == null) {
			root = newNode;
			return true;
		}
		Node f = null; // 指向父结点
		Node p = root; // 当前结点的指针
		while (p != null) {
			if (p.data > key) {
				f = p;
				p = p.lChild;
			} else if (p.data < key) {
				f = p;
				p = p.rChild;
			} else {
				System.out.println("数据重复，无法插入！");
				return false;
			}
		}
		if (f.data > key) {
			f.lChild = newNode;
		} else if (f.data < key) {
			f.rChild = newNode;
		}
		return true;
	}

	/*
	 * 插入，参考别人博客，递归
	 * 思路：类似查找，
	 *       但若方法中的node为null的话，将无法插入新数据，需排除null的情况
	 */
	public boolean InsertBST2(int key) {
		if (root == null) {
			root = new Node(key);
			return true;
		}
		return InsertBST2(key, root);
	}

	private boolean InsertBST2(int key, Node node) {
		if (node.data > key) {
			if (node.lChild == null) { // 有null的情况下，才有父结点
				node.lChild = new Node(key);
				return true;
			} else {
				return InsertBST2(key, node.lChild);
			}
		} else if (node.data < key) {
			if (node.rChild == null) {
				node.rChild = new Node(key);
				return true;
			} else {
				return InsertBST2(key, node.rChild);
			}
		} else {
			System.out.println("数据重复，无法插入！");
			return false;
		}
	}

	/*
	 * 这样的插入是错误的（node无法真正被赋值）
	 */
	/*
	private boolean InsertBST2(int key, Node node) {
		if(node!=null) {
			if (node.data > key) 
				return InsertBST2(key, node.lChild);
			else if (node.data < key) 
				return InsertBST2(key, node.rChild);
			else 
				return false;//重复
		}else {
			node=new Node(key);
			return true;
		}			
	}
	*/

	/*
	 * 删除操作，先找到删除结点位置及其父结点
	 * 因为需要有父结点，所以暂时没想到递归的方法（除了令Node对象带个parent属性）
	 */
	public boolean deleteBST(int key) {
		if (root == null) {
			System.out.println("空表，删除失败");
			return false;
		}
		Node f = null; // 指向父结点
		Node p = root; // 指向当前结点
		while (p != null) {
			if (p.data > key) {
				f = p;
				p = p.lChild;
			} else if (p.data < key) {
				f = p;
				p = p.rChild;
			} else {
				delete(p, f);
				System.out.println("删除成功！");
				return true;
			}
		}
		System.out.println("该数据不存在");
		return false;
	}

	/*
	 * 删除结点P的操作
	 * 必须要有父结点,因为Java无法直接取得变量p的地址（无法使用*p=(*p)->lChild）
	 */
	private void delete(Node p, Node f) {// p为删除结点，f为其父结点
		if (p.lChild == null) { // 左子树为空，重接右子树
			if (p == root) { // 被删除结点为根结点，该情况不能忽略
				root = root.rChild;
				p = null;
			} else {
				if (f.data > p.data) { // 被删结点为父结点的左结点，下同
					f.lChild = p.rChild;
					p = null; // 释放结点别忘了
				} else {// 被删结点为父结点的右结点，下同
					f.rChild = p.rChild;
					p = null;
				}
			}
		} else if (p.rChild == null) { // 右子树为空，重接左子树
			if (p == root) { // 被删除结点为根结点
				root = root.lChild;
				p = null;
			} else {
				if (f.data > p.data) {
					f.lChild = p.lChild;
					p = null;
				} else {
					f.rChild = p.lChild;
					p = null;
				}
			}
		} else { // 左右子树都不为空,删除位置用前驱结点替代
			Node q, s;
			q = p;
			s = p.lChild;
			while (s.rChild != null) { // 找到待删结点的最大前驱s
				q = s;
				s = s.rChild;
			}
			p.data = s.data; // 改变p的data就OK
			if (q != p) {
				q.rChild = s.lChild;
			} else {
				q.lChild = s.lChild;
			}
			s = null;
		}
	}

	/*
	 * 中序遍历
	 */
	public void inOrder() {
		inOrder(root);
		System.out.println();
	}

	public void inOrder(Node node) {
		if (node == null)
			return;
		inOrder(node.lChild);
		System.out.print(node.data + " ");
		inOrder(node.rChild);
	}

	/*
	 * 测试代码
	 */
	public static void main(String[] args) {
		BSTree aTree = new BSTree();
		BSTree bTree = new BSTree();
		int[] arr = { 62, 88, 58, 47, 35, 73, 51, 99, 37, 93 };
		for (int a : arr) {
			aTree.InsertBST(a);
			bTree.InsertBST2(a);
		}
		aTree.inOrder();
		bTree.inOrder();
		System.out.println(aTree.SearchBST(35));
		System.out.println(bTree.SearchBST2(99));
		aTree.deleteBST(47);
		aTree.inOrder();
	}
}

　　

35 37 47 51 58 62 73 88 93 99 
35 37 47 51 58 62 73 88 93 99 
true
true
删除成功!
35 37 51 58 62 73 88 93 99 

 

 小结（自己编写时的注意点）：

　　查找：操作简单，注意递归的方法没有循环while (p!=null)，而是并列的几个判断；

　　插入：非递归时，要有父结点；递归时，要注意排除null的情况；

　　删除：记住要分两步，第一步找结点位置时也要把父结点带上；第二步删除结点时，要令p=null，还要注意p==root的情况以及q==p的情况。