【Java】 大话数据结构(9) 树(二叉树、线索二叉树)
本文根据《大话数据结构》一书,对Java版的二叉树、线索二叉树进行了一定程度的实现。
另:
二叉树的性质
性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
证明提示:分支线总数=n0+n1+n2-1=n1+2×n2
性质4:具有n个节点的完全二叉树的深度为[log2n]+1。([ ]代表向下取整)
证明提示:假设深度为k,则有2{k-1} -1<n≤2{k} -1。
性质5:如果有一颗有n个节点的完全二叉树的节点按层次序编号,对任一层的节点i(1<=i<=n)有
1.如果i=1,则节点是二叉树的根,无双亲,如果i>1,则其双亲节点为[i/2]
2.如果2i>n那么节点i没有左孩子(叶子结点),否则其左孩子为2i
3.如果2i+1>n那么节点没有右孩子,否则右孩子为2i+1
二叉链表的定义代码
class BiTNode<E>{
E data;
BiTNode<E> lchild,rchild;
public BiTNode(E data) {
this.data=data;
this.lchild=null;
this.rchild=null;
}
}
public class BiTree<E> {
private BiTNode<E> root;
public BiTree() {
root=null;
}
...
}
二叉树的遍历
/*
* 前序遍历
*/
public void preOrder() {
preOrderTraverse(root);
System.out.println();
}
private void preOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
System.out.print(node.data);
preOrderTraverse(node.lchild);
preOrderTraverse(node.rchild);
}
/*
* 中序遍历
*/
public void inOrder() {
inOrderTraverse(root);
System.out.println();
}
private void inOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
inOrderTraverse(node.lchild);
System.out.print(node.data);
inOrderTraverse(node.rchild);
}
/*
* 后序遍历
*/
public void postOrder() {
postOrderTraverse(root);
System.out.println();
}
private void postOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
postOrderTraverse(node.lchild);
postOrderTraverse(node.rchild);
System.out.print(node.data);
}
二叉树的建立
《大话》一书中,6.9节关于二叉树的建立如下:
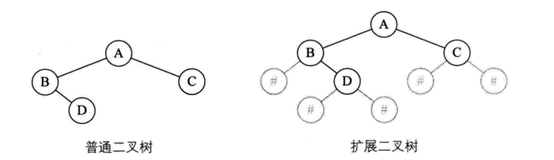
通过输入AB#D##C##,可以生成上述二叉树,其C语言的实现算法如下:


暂时能力有限,还不懂如何改为Java代码。
几点疑问:1.exit(OVERFLOW)不是很清楚什么意思;
2.代码中为char类型,如何用于泛型?
3.scanf()在Java中怎么实现?用scanner吗?程序如何知道输入完“AB#D##C##”就结束二叉树的构造呢?总的实现代码(包括main部分)是怎么样的?
以下为测试代码遍历的总体测试代码:
package BiTree;
class BiTNode<E>{
E data;
BiTNode<E> lchild,rchild;
public BiTNode(E data) {
this.data=data;
this.lchild=null;
this.rchild=null;
}
}
public class BiTree<E> {
private BiTNode<E> root;
public BiTree() {
//root=new BiTNode(null, null, null);
root=null;
}
/*
* 前序遍历
*/
public void preOrder() {
preOrderTraverse(root);
System.out.println();
}
private void preOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
System.out.print(node.data);
preOrderTraverse(node.lchild);
preOrderTraverse(node.rchild);
}
/*
* 中序遍历
*/
public void inOrder() {
inOrderTraverse(root);
System.out.println();
}
private void inOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
inOrderTraverse(node.lchild);
System.out.print(node.data);
inOrderTraverse(node.rchild);
}
/*
* 后序遍历
*/
public void postOrder() {
postOrderTraverse(root);
System.out.println();
}
private void postOrderTraverse(BiTNode<E> node) {
if(node==null)
return;
postOrderTraverse(node.lchild);
postOrderTraverse(node.rchild);
System.out.print(node.data);
}
/*
* 6.9 二叉树的建立暂时不会,略
*/
public static void main(String[] args) {
BiTree<String> aBiTree = new BiTree<String>();
aBiTree.root=new BiTNode("A");
aBiTree.root.lchild=new BiTNode("B");
aBiTree.root.rchild=new BiTNode("C");
aBiTree.root.lchild.rchild=new BiTNode("D");
System.out.println("————前序————");
aBiTree.preOrder();
System.out.println("————中序————");
aBiTree.inOrder();
System.out.println("————后序————");
aBiTree.postOrder();
}
}

————前序————
ABDC
————中序————
BDAC
————后序————
DBCA
线索二叉树
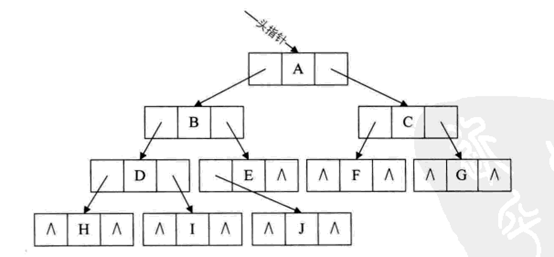
对一个有n个节点的二叉链表(如上图),整表存在2n个指针域,但分支线只有n-1条,说明空指针域的个数为2n-(n-1) = n+1个,浪费了很多的内存资源。
我们可以通过利用这些空指针域,存放节点在某种遍历方式下的前驱和后继节点的指针。我们把这种指向前驱和后继的指针成为线索,加上线索的二叉链表成为线索链表,对应的二叉树就成为“线索二叉树(Threaded Binary Tree)”,如下图所示。
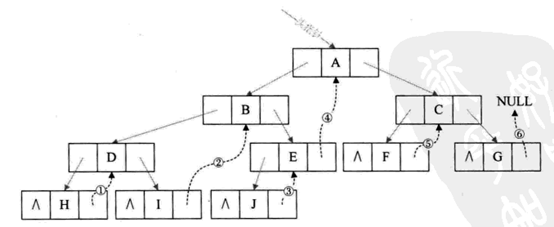
线索二叉树的Java代码如下:
package BiThrTree;
/**
* 线索二叉树
* 包含二叉树的中序线索化及其遍历
* @author Yongh
*
*/
class BiThrNode<E>{
E data;
BiThrNode<E> lChild,rChild;
boolean lTag,rTag;
public BiThrNode(E data) {
this.data=data;
//tag都先定义成左右孩子指针。
lTag=false; //其实把Tag定义为IsThread更好
rTag=false;
lChild=null;
rChild=null;
}
}
public class BiThrTree<T> {
BiThrNode<T> root;
boolean link=false,thread=true;
public BiThrTree() {
root=null;
}
/*
* 中序线索化二叉树
* 即:在遍历的时候找到空指针进行修改。
*/
BiThrNode<T> pre; //线索化时记录的前一个结点
public void inThreading() {
inThreading(root);
}
private void inThreading(BiThrNode<T> p) {
if(p != null) {
inThreading(p.lChild);
if(p.lChild==null) {
p.lTag=thread;
p.lChild=pre;
}
if(pre!=null && pre.rChild==null) { //pre!=null一定要加上
pre.rTag=thread;
pre.rChild=p;
}
pre=p; //别忘了在这个位置加上pre=p
inThreading(p.rChild);
}
}
/*
* 中序遍历二叉线索链表表示的二叉树(按后继方式)
* 书中添加了一个头结点,本程序中不含头结点
* 思路:先找到最左子结点
*/
public void inOrderTraverse() {
BiThrNode<T> p = root;
while(p!=null) {
while(p.lTag==link)
p=p.lChild; //找到最左子结点
System.out.print(p.data);
while(p.rTag==thread) { //不是if
p=p.rChild;
System.out.print(p.data);
}
p=p.rChild;
}
System.out.println();
}
/*
* 中序遍历方法二(按后继方式)
* 参考别人的博客
*/
public void inOrderTraverse2() {
BiThrNode<T> node = root;
while(node != null && node.lTag==link) {
node = node.lChild;
}
while(node != null) {
System.out.print(node.data + ", ");
if(node.rTag==thread) {//如果右指针是线索
node = node.rChild;
} else { //如果右指针不是线索,找到右子树开始的节点
node = node.rChild;
while(node != null && node.lTag==link) {
node = node.lChild;
}
}
}
System.out.println();
}
public static void main(String[] args) {
BiThrTree<String> aBiThrTree = new BiThrTree<String>();
aBiThrTree.root=new BiThrNode<String>("A"); // A
aBiThrTree.root.lChild=new BiThrNode<String>("B"); // / \
aBiThrTree.root.lChild.lChild=new BiThrNode<String>("C"); // B D
aBiThrTree.root.rChild=new BiThrNode<String>("D"); // / / \
aBiThrTree.root.rChild.lChild=new BiThrNode<String>("E"); // C E F
aBiThrTree.root.rChild.rChild=new BiThrNode<String>("F");
aBiThrTree.inThreading();
aBiThrTree.inOrderTraverse();
aBiThrTree.inOrderTraverse2();
}
}

CBAEDF
C, B, A, E, D, F,
推荐阅读:
线索二叉树原理及前序、中序线索化(Java版)(文中对线索二叉树的介绍和代码都比较清晰,且更加全面)。
赫夫曼树及其应用
带权路径长度WPL最小的二叉树称为最优二叉树,也称为赫夫曼树(Huffman Tree)。

赫夫曼编码:

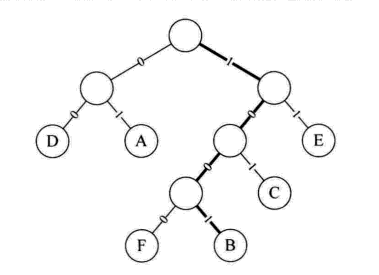
推荐阅读:哈夫曼树(三)之 Java详解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号