学习笔记_西瓜书（周志华 机器学习）&&慕课视频(机器学习by蒋良孝、胡成玉）（学习中。。。）

感觉未来是大数据环境下的人工智能时代呀，不能被时代的马车抛弃，西瓜书这么出名，简要了解一下

1 绪论

1.1 引言

机器学习定义：利用经验来改善计算机系统自身的性能

  另外一种广泛被引用的英文定义：A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E（T：任务，P：性能评估，E：数据，一段程序利用E提升了在T上的P那么就称之为机器学习）

机器学习的主要内容即在数据中产生模型的算法

机器学习的核心即学习算法

机器学习动机：为了让计算机系统具有人的学习能力以便实现人工智能

机器学习技术：神经网络学习、决策树学习、贝叶斯学习、最近邻学习、线性学习、支持向量机学习等等

经验在计算机中的表现为数据，那么使得机器学习成为智能分析技术的创新源之一，并且因此受到越多关注

经常和另外一种智能分析技术-数据挖掘来对比

数据挖掘：识别出巨量数据中有效的、新颖的、潜在有用的、最终可理解的模式的非平凡过程

数据挖掘可以视为机器学习与数据库的交叉，主要利用机器学习界提供的技术来分析海量数据，利用数据库界的技术来管理海量数据

机器学习和数据挖掘既有区别又有联系，机器学习偏理论，数据挖掘偏应用

1.2 基本术语

数据集(dataset):类比数据库概念中的table

示例(instance) or 样本(sample):类比数据库中table中的row即一行记录或称之为元组，在空间中也可以描述为特征向量(feature vector)

属性(attr) or 特征(feature):类比数据库中的col即列，空间中也叫做维数(dimensionality)

属性空间、样本空间、输入空间：属性值的取值集合

学习或者训练：从数据中产生模型的过程

训练数据

训练样本

训练集

标记(lable):关于示例结果的信息

样例(example):拥有了标记信息的示例

标记空间(lable space) or 输出空间：所有标记的集合

分类(classification)：预测的是离散值

回归(regression):预测的连续值

聚类(clustering)

二分类：预测值只有两个，一个叫正类，一个叫反类

多分类：预测值多于2

测试：学得模型后，利用模型预测的过程

有监督学习：数据集有标记（分类和回归算法属于此）

无监督学习：数据集没有标记（聚类算法属于此）

泛化（generalization):学得的模型适用于新样本的能力

1.3 假设空间

归纳(induction):特殊到一般，泛化过程(generalization)

演绎(deduction)：一般到特殊(specilization)

概念学习、布尔概念学习：研究、应用较少，因为学得语义明确泛化性能好的概念太难了

机械学习

样本噪声

学习：在假设空间进行搜索的过程

假设集合、假设空间、版本空间

1.4 归纳偏好

“奥卡姆剃刀”：若有多个假设与观察一致，则选择最简单的那个

算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得好的性能

“没有免费午餐”定理，即NFL定理：在脱离实际意义情况下，空泛地谈论哪种算法好毫无意义，要谈论算法优劣必须针对具体学习问题

1.5 发展历程

机器学习是人工智能研究发展到一定阶段的必然产物

1.6 应用现状

应用广泛

“只要有数据存在的地方，机器学习就有价值”

2 模型评估与选择

2.1 经验误差与过拟合

错误率

精度

误差

训练误差

泛化误差

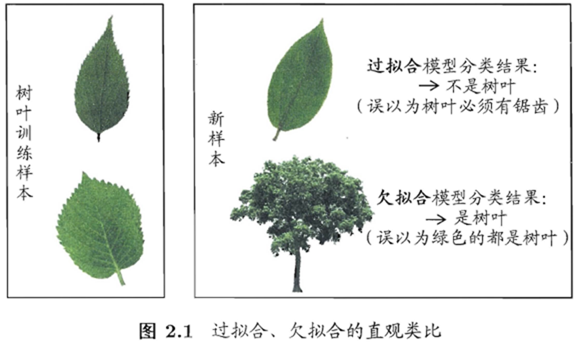
过拟合：学习能力太强，除了训练样本中的“一般规律”学到了，连不太一般的特性也学到了

欠拟合：学习能力弱

欠拟合比较容易克服，例如在决策树学习中扩展分支、在神经网络学习中增加训练轮数等；而过拟合则很麻烦，是机器学习面临的关键障碍，是无法避免的，我们只能“减缓”或者减少其风险

机器学习面临的问题通常是NP困难甚至更难，有效的学习算法必然是在多项式时间内运行完成

实际中，不同算法甚至相同算法不同调参都产生不同模型，那么使用哪个就是“模型选择”问题

2.2 评估方法

测试集

测试误差：用来当作泛化误差的近似

留出法：一般要多次随机划分重复实验取均值，通常做法是2/3-4/5样本用于训练

p次k折交叉验证法：常见的10次10折交叉验证法

自助法：数据量少时候有用

调参

验证集

2.3 性能度量

性能度量：对学习器的泛化性能评估

均方误差：回归任务最常用的性能度量

错误率

精度

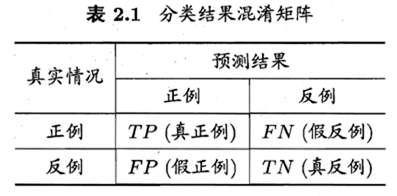
查准率precision

  P=TP/(TP+FP)

查全率recall

  R=TP/(TP+FN)

查准率-查全率曲线，即P-R曲线

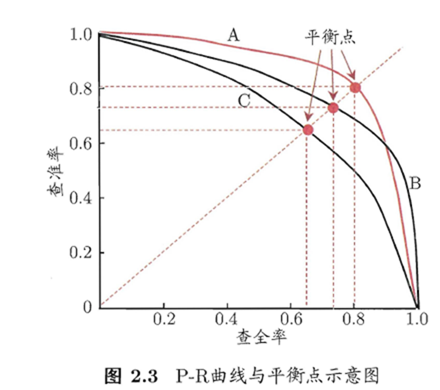如果一个学习器的P-R曲线被另一个学习器的P-R曲线包住，则断定后者性能更好，如果有交叉，则难以断定需要个性化权衡P和R，如果仍然比较优劣，合理的判断是比较面积大小

平衡点，是查准率=查全率的取值，以此点比较学习器的优劣

F1度量：平衡点还是过于简单，F1更常用

F_β=（1+β²）*P*R/((β²*P)+R)

当β=1时候为标准的F1

F1=2*P*R/(P+R)

其中，β>0度量了查全率对查准率的相对重要性，β>1时，查全率更重要,β<1，查准率更重要

多次训练/测试得出宏查准率、宏查全率、微查准率、微查全率

---

ROC曲线:受试者工作特征

纵轴：真正利率TPR=TP/(TP+FN)

横轴：假正利率FPR=FP/(TN+FP)

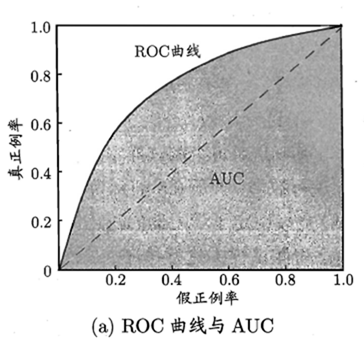
某个学习器的ROC曲线被另一个学习器完全包住，则后者更优；弱有交叉，则判断下方面积AUC

---

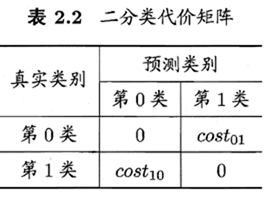
代价敏感错误率与代价曲线

非均等代价

代价矩阵

非均等代价情况下用代价曲线替换ROC曲线

2.4 比较检验

统计假设检验(hypothesis test)：假设检验、交叉验证t检验、McNemar检验、Friedman检验与Nemenyi后续检验

2.5 方差与偏差

“偏差-方差分解”是解释学习算法泛化性能的一种重要工具

3 线性模型

3.1 基本形式

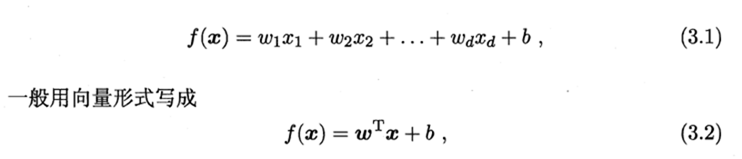
易解释，直观表达各个属性的重要性

3.2 线性回归

均方误差 or 平方损失  or 残差：最小

最小二乘法：试图找到一条直线，使得所有样本到直线上的欧式距离最小

简单回归

多元线性回归

待续