二维前缀和及差分

参考资料

https://www.acwing.com/blog/content/5890/
https://chen-ac.blog.csdn.net/article/details/115844025

二维前缀和

假设我们给定义个二维数组a以及一个坐标(x,y）,我们把它左上角的所有元素的和叫做a在（x,y）的前缀和，定义出这样子的一个二维数组，那它就是前缀和数组。

前缀和数组求法:

sum[x][y]=sum[x-1][y]+sum[x][y-1]+a[x][y];

可以用面积来理解，（0，0）->(x，y)的面积=红色围住的面积+蓝色围住的面积—重叠部分的面积

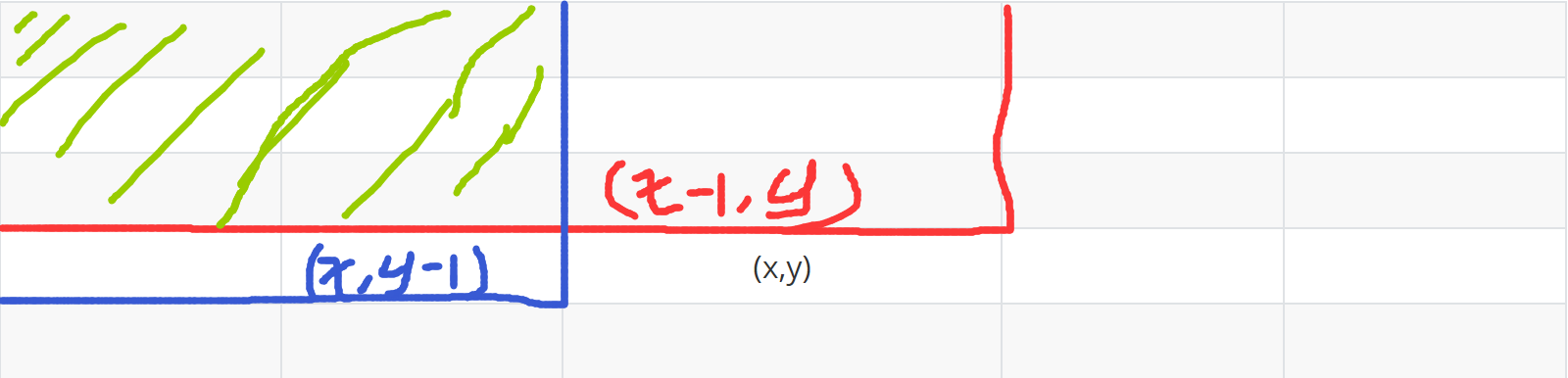
求部分矩阵和

假设我给出前缀和数组，给定两个点（x1,y1）和（x2,y2），他们分别表示一个矩形的左上角和右下角（x1,y1）和（x2,y2），求两点之间的矩形所有的数的和。理解的话看下图，这里给出具体公式：

all=sum[x2][y2]-sum[x2][y1-1]-sum[x1-1,][y2]+sum[x-1][y-1];

二维差分

具体差分数组是怎样定义的好像我也不懂，但这并不影响。
同样的，二位差分数数组适用的条件也是有范围的，我们在一维差分里，我们应用差分数组的条件是在一个连续段上加上或减去某一个数。
在二维中，我们的条件是对一个矩形内的内容进行操作。

下图以及相应引用来自SolitudeAlma

从图中我们可以很清楚的看到，如果在x1，y1上加一个数c那么它右下角的数都会加上c，那么该怎么办呢，其实这也是容斥定理。我们只需要减去右边多加的部分和下边多加的部分最后再加上重复减去的部分即可

所以，我们对二位差分数组进行的操作如下：

add(int x1,int y1,int x2,int y2,int c){
	dif[x1][y1]+=c,dif[x2+1][y2+1]+=c;
	dif[x2+1][y1]-=c,dif[x1][y1+1]-=c;
}

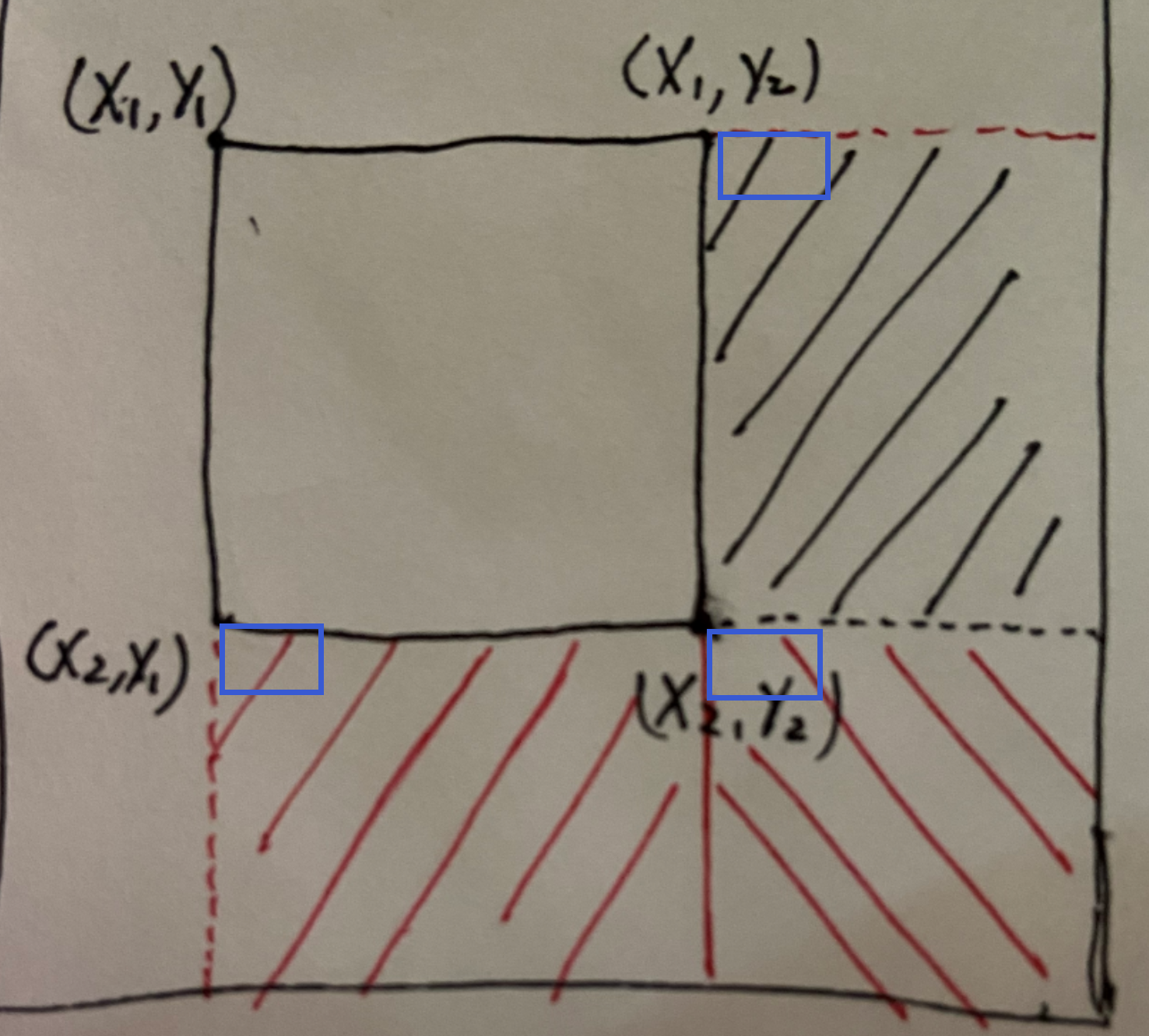
我只要在图中带框的位置进行加减操作就不会影响到矩形外的元素了