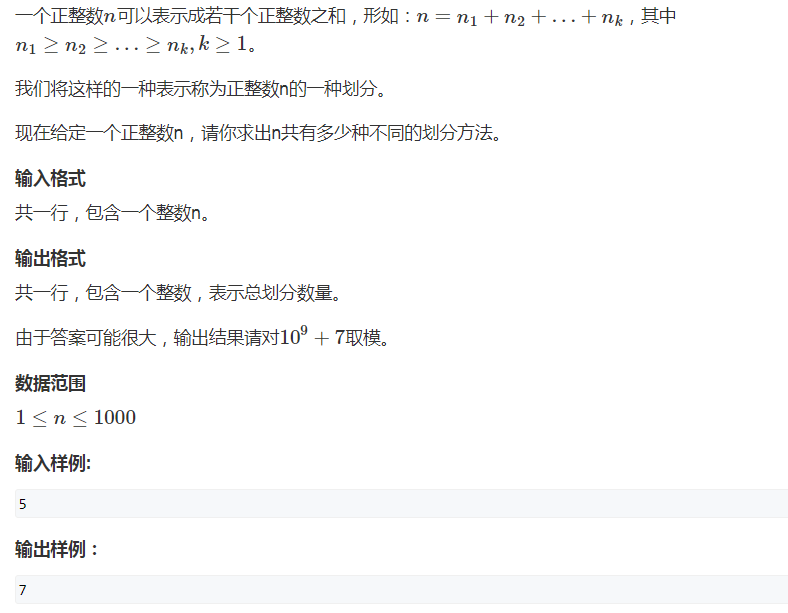
900. 整数划分（动态规划）

 

 方法一： 背包模型

#include <bits/stdc++.h>
using namespace std;

const int N = 10010, mod = 1e9 + 7;
int dp[N][N];
int n;

int main() {
    scanf("%d",&n);
    for(int i = 1; i <= n; i++) dp[i][0] = 1;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(j >= i) {
                dp[i][j] = (dp[i-1][j] + dp[i][j-i]) % mod;
            } else {
                dp[i][j] = dp[i-1][j];
            }
        }
    }
    printf("%d\n",dp[n][n]);
    return 0;
}

方法二：

#include <bits/stdc++.h>
using namespace std;

const int N = 10010, mod = 1e9 + 7;
int dp[N][N];
int n;

int main() {
    scanf("%d",&n);  // dp[i][j]:总数为i，分为j组的方案数
    dp[0][0] = 1;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= i; j++) {
                        // 两种集合划分
                        //有1         // 没有1
            dp[i][j] = (dp[i-1][j-1] + dp[i-j][j]) % mod;
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i++) res = (res + dp[n][i]) % mod;
    printf("%d\n",res);
    return 0;
}