P7689 [CEOI2002] Bugs Integrated,Inc 题解

博客园食用更佳

题目描述

给一个 N * M 的矩阵，其中有些点不能被使用，问这个矩阵一共可以放多少个 2 * 3 长方形。可以横着，也可以竖着。

对于 \(100 \%\) 的数据，\(1 \leq D \leq 5\)，\(1 \leq N \leq 150\)，\(1 \leq M \leq 10\)，\(0 \leq K \leq M×N\)，\(1 \leq x \leq N\)，\(1 \leq y \leq M\) 。

题目分析

思路分析

看到这道题第一反应是 蒙德里安的梦想 ，很像，只是这道题放的长方形大小不太一样。

那道题的一个做法是状压 DP ，每行状态二进制中 1 表示一个骨牌的上半部分（即这个骨牌一定竖着放），0 代表其他情况。最后答案是 f[n][0] 。

再看这道题数据范围，M 很小，八九不离十是状压 DP 了。仿照上面的做法，会发现由于长方形大小的原因，单纯的二进制似乎无法满足所有要求。

横着放只有 2 行可以表示，但竖着放时就有 3 行。那可以自然地想到 3 进制。

可以这样表示：

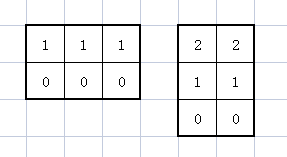
然后可以枚举每一行，从上一行的可行状态来考虑枚举这一行的符合条件的所有状态，再更新。

---

枚举状态细节

1. 如果上一行当前位置有值，但这个点不能用，直接返回。
2. 如果当前点不能用，为 0 。
3. 如果上一行的当前位置非零，为上一行的值 -1 。
4. 如果上一行这个位置即后面两个位置都为零，且这一行这几个点都可用，可以一起设为 1 。
5. 如果上一行这个位置即后面一个位置都为零，且这一行这几个点都可用，可以一起设为 2 。
6. 这个位置为 0 。

先满足前三个，如果是前三个的一种， dfs 完直接返回。

否则枚举完剩下三种情况。具体见代码。

因为空间范围很小，所以滚动一下数组。

Code

#include<bits/stdc++.h>
//By _yolanda_
using namespace std;
#define int long long

const int N=6e4+5,INF=1e15;
int f[2][N],w[200][20];
int n,m;
int in[15];

inline int read(){
	int sum=0,f=1;char a=getchar();
	while(a<'0' || a>'9'){if(a=='-') 	f=-1;a=getchar();}
	while(a>='0' && a<='9') 	sum=sum*10+a-'0',a=getchar();
	return sum*f;
}

inline int get(int x,int y){ //找3进制下x的第y位
	int tmp=in[y];
	return (x/tmp)%3;
}
void dfs(int x,int y,int no,int pre,int sum){
	if(y==m){//到边界，更新
		f[x%2][no]=max(f[(x%2)^1][pre]+sum,f[x%2][no]);
		return;
	}
	int t=get(pre,m-y-1); //上一行，这个位置的值
	if(w[x][y+1]){ //这个位置不能用
		if(t)	return;
		dfs(x,y+1,no*3,pre,sum);
	}
	else if(t){
		dfs(x,y+1,no*3+t-1,pre,sum);//第3种情况
	}
	else{
		if(x<n && m-y>=3 && !get(pre,m-y-2) && !get(pre,m-y-3) && !w[x][y+2] && !w[x][y+3]){
			int tmp=no*3+1;tmp=tmp*3+1,tmp=tmp*3+1;
			dfs(x,y+3,tmp,pre,sum+1);
		}//连着填3个1
		if(x<n-1 && m-y>=2 && !get(pre,m-y-2) &&!w[x][y+2]){
			int tmp=no*3+2;tmp=tmp*3+2;
			dfs(x,y+2,tmp,pre,sum+1);
		}//连着填3个2
		dfs(x,y+1,no*3,pre,sum);//填0
	}
}

signed main(){
	
	in[0]=1;
	for(int i=1;i<=10;++i)	in[i]=in[i-1]*3;
	int T,k;T=read();
	while(T--){
		memset(w,0,sizeof w);
		memset(f,0,sizeof f);
		n=read(),m=read(),k=read();
		
		int tp=pow(3,m);
		int xx,yy;
		for(int i=1;i<=k;++i){
			xx=read(),yy=read();
			w[xx][yy]=1;
		}
		dfs(1,0,0,0,0);
		for(int i=2;i<=n;++i){
			for(int j=0;j<tp;++j)	f[i%2][j]=-INF;
			for(int j=0;j<tp;++j)
				if(f[(i-1)%2][j]>=0)	dfs(i,0,0,j,0);
				//上一行这个状态可得到才更新，否则会TLE
		}
		printf("%lld\n",f[n%2][0]);
	}
	
	return 0;
}