[Deep Learning] 神经网络编程基础 (Basics of Neural Network Programming) - 逻辑回归-梯度下降-计算图
在神经网络中,假如有m个训练集,我们想把他们加入训练,第一个想到得就是用一个for循环来遍历训练集,从而开始训练。但是在神经网络中,我们换一个计算方法,这就是 前向传播和反向传播。
对于逻辑回归,就是找出合适得参数w和b,在二分类中,输出得结果是0或者1,所以我们得假设函数得输出应该在0,1之间。那么线性肯定是不合适的。我们称输出结果在0,1之间的函数为 S 函数(sigmoid 函数)。

那么逻辑回归的代价函数又是什么呢? 为了训练逻辑回归模型的参数参数𝑥和参数𝑐我们,需要一个代价函数,通过训练代价函数来得到参数𝑥和参数𝑐。
那么 如何衡量预测值和实际值的误差呢? 这里我们用损失函数来表示。
在逻辑回归中用到的损失函数为:![]()
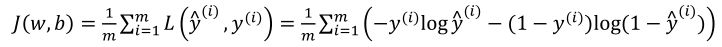
我们可以衡量预测值和实际值之间的关系了,那么我们如何找到最合适的w和b呢? 这里我们需要用到梯度下降法。
在上图中的J(w,b)应该是一个凸函数,如果是下图的函数,是一个非凸函数且有很多局部最小值,那我们是无法用梯度下降法获取到最合适的参数值。

所以我们必须定义代价函数为凸函数。
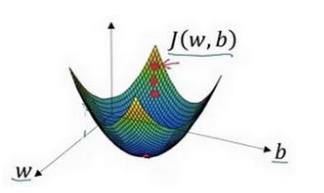
其中,学习率依然表示步长。
上面说,前向传播和反向传播是为了帮助我们计算神经网络,这里我们来看一下是如何帮我们计算的。
首先,我们先把一个神经网络计算画成一个计算图。
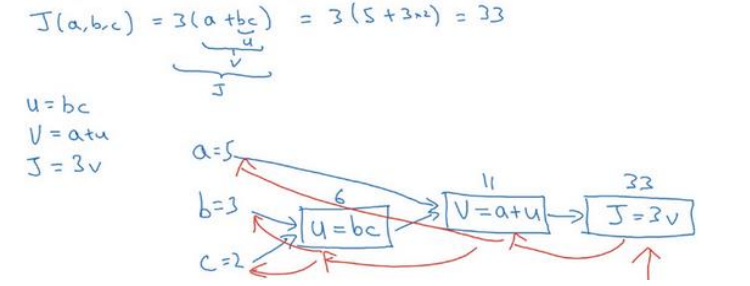
我们尝试计算函数𝐾,𝐾是由三个变量a,b,c组成的函数,这个函数是3(a + bc) 。计算这个函数实际上有三个不同的步骤,首先是计算 b 乘以 c,我们把它储存在变量u中,因此u = bc; 然后计算v = a + u;最后输出J = 3v,这就是要计算的函数J。我们可以把这三步
画成如下的计算图,我先在这画三个变量a,b,c,第一步就是计算u = bc,我在这周围放个矩形框,它的输入是b,c,接着第二步v = a + u,最后一步J = 3𝑤。
举个例子: 𝑏 = 5,b = 3,c = 2 ,u = bc就是 6,就是 5+6=11。J是 3 倍的 ,因此。即3 × (5 + 3 × 2)。如果你把它算出来,实际上得到 33 就是J的值。 当有不同的或者一些特殊的输出变量时,例如本例中的J和逻辑回归中你想优化的代价函数J,因此计算图用来处理这
些计算会很方便。从这个小例子中我们可以看出,通过一个从左向右的过程,你可以计算出𝐾的值。为了计算导数,从右到左(红色箭头,和蓝色箭头的过程相反)的过程是用于计算导数最自然的方式。
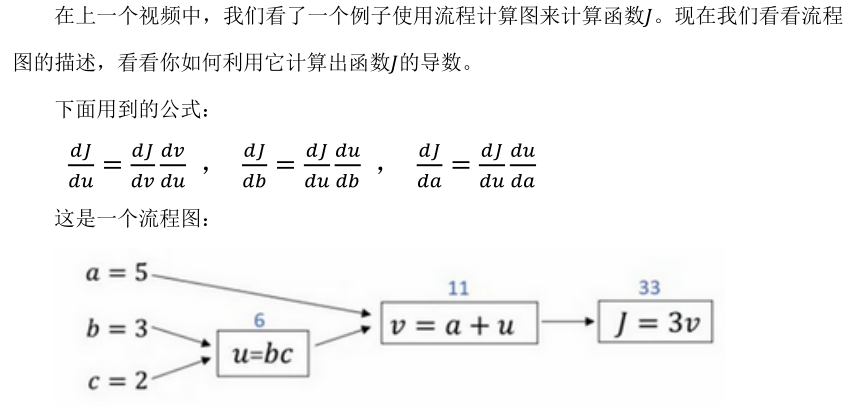

依此类推,我们可以计算出 dJ/da=3 dJ/db=6 dJ/dc=9
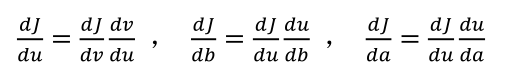
linux内核下载地址: https://www.kernel.org/pub/linux/kernel



