[Machine Learning] 逻辑回归 (Logistic Regression) -分类问题-逻辑回归-正则化

　　在之前的问题讨论中，研究的都是连续值，即y的输出是一个连续的值。但是在分类问题中，要预测的值是离散的值，就是预测的结果是否属于某一个类。例如：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；之前我们也谈到了肿瘤分类问题的例子，区别一个肿瘤是恶性的还是良性的。

　　我们先说二分类问题，我们将一些自变量分为负向类和正向类，那么因变量为0，1；0表示负向类，1表示正向类。

　　如果用线性回归来讨论分类问题，那么假设输出的结果会大于1，但是我们的假设函数的输出应该是在0，1之间。所以我们把输出结果在0，1之间的算法叫做逻辑回归算法。

　　因为线性回归算法中，函数的输出肯定会大约1，所以我们定义了一个新的函数来作为分类问题的函数，我们用g代表逻辑函数，它通常是一个S形函数，公式为：

Python代码：

import numpy as np
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

　　函数图像为：

 

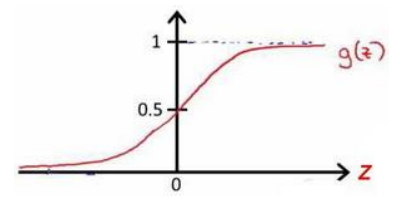
这样，无论自变量取值是多少，函数的输出值一直在0，1之间。

 

在线性回归模型中，我们定义的代价函数是所有模型误差的平方和。当在逻辑回归模型中，如果还延用这个定义，将代入，我们得到是一个非凸函数：

 

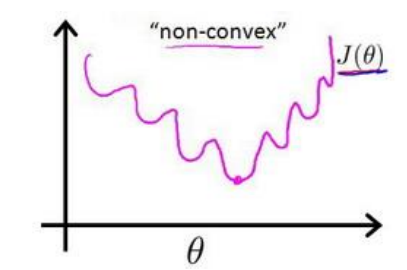
 这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

　　我们重新定义逻辑回归的代价函数为：，其中 。

 

 

Python代码：

import numpy as np
def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
    return np.sum(first - second) / (len(X))

　　

 在多分类问题，我们遇到的问题是一对多。而相对于而分类来说，在多分类中，我们可以把相近的认为是一类，把一个多分类问题认为是多个二分类问题，从而实现多分类问题的解决方案。

 

 在回归问题中，还有一个过拟合的问题，如下图所示：

 

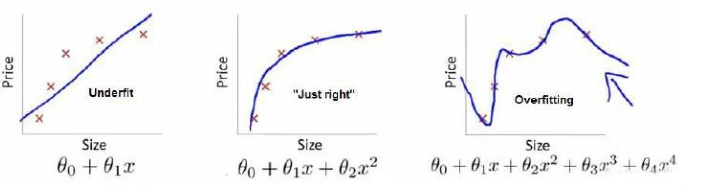
上图中，只有图二比较好，第一个图型是欠拟合，第三个是过拟合：过去强调拟合原始数据而丢失了算法的本质。

那么解决上述的问题有两个方法：

1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如 PCA）
2.正则化。 保留所有的特征，但是减少参数的大小（magnitude）。

在回归问题中，出现过拟合的原因是因为高阶系数太大了，如果让高阶系数接近0的话就可以解决这个问题了。所以要做的就是在一定程度上减小这些参数的值，这就是正则化的基本方法。

对于一个代价函数，我们修改后的结果如下：。

 

如果我们不知道哪些特征需要惩罚，我们将对所有的特征进行惩罚，并让代价函数最优软件来选择这些惩罚的程度。

 

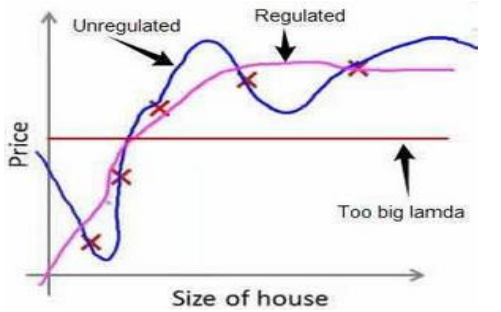
 其中的λ称为正则化参数，如果选择的正则化参数 λ 过大，则会把所有的参数都最小化了，导致模型变成 ℎ𝜃(𝑦) =𝜃0 ，也就是上图中红色直线所示的情况，造成欠拟合。

𝜃0 不参与其中的任何一个正则化。