[Machine Learning] 多变量线性回归(Linear Regression with Multiple Variable)-特征缩放-正规方程
我们从上一篇博客中知道了关于单变量线性回归的相关问题,例如:什么是回归,什么是代价函数,什么是梯度下降法。
本节我们讲一下多变量线性回归。依然拿房价来举例,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(x0 ,x1 ,...,xn )。
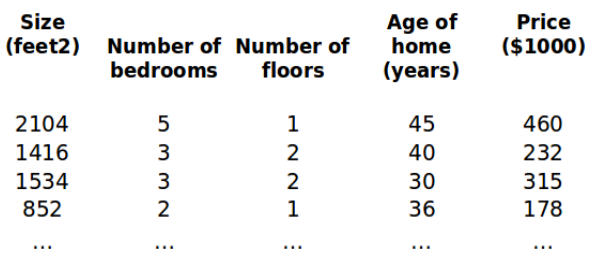
增添更多特征后,我们引入一系列新的注释:

假设函数 h 表示为:
这个公式中有 n+1个参数和 n 个变量,为了使得公式能够简化一些,引入x0 = 1,则公
式转化为:![]()
此时模型中的参数是一个 n+1维 的向量,任何一个训练实例也都是 n+1维的向量,特
征矩阵X的维度是m*(n+1)。因此公式可以简化为:![]() 。
。
和单变量线性回归类似,在多变量线性回归中,构建一个代价函数,也是所有建模误差的平方和,即:![]() 。其中
。其中![]() 。
。
使用梯度下降算法为:

代码示例:
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
在多变量中有个问题,就是每个变量的取值范围不是一样的,比如 一套房子的房间数量大概是 0-5, 而尺寸大约为 0-200平方米,如果以上述的两个取值范围代入代价函数进行计算的话,整个计算权重就会偏移,所以我们把所有变量的取值范围归一到 [-1,1]之间,那么 把变量的取值范围归一的步骤就叫 特征缩放。对于有些数据可能需要平方或者是三次方的操作,我们也可以归一化,把三次方去掉,从而转化为线性回归。特征缩放 可以加快梯度下降。
对于学习率,梯度下降算法的每次迭代受到学习率的影响,如果学习率𝑏过小,则达到收敛所需的迭代次数会非常高;如如果学习率𝑏过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试这些学习率:
a= 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10
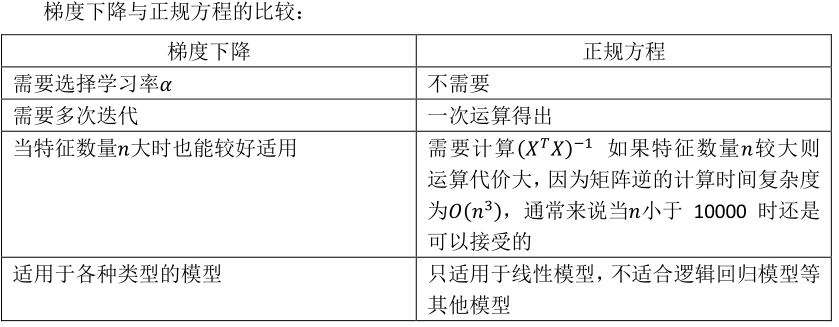
对于某些线性回归问题,可以使用正规方程来解算。

正规方程解出向量 :![]() 。
。
注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。
正规方程![]() 的推算过程:
的推算过程:

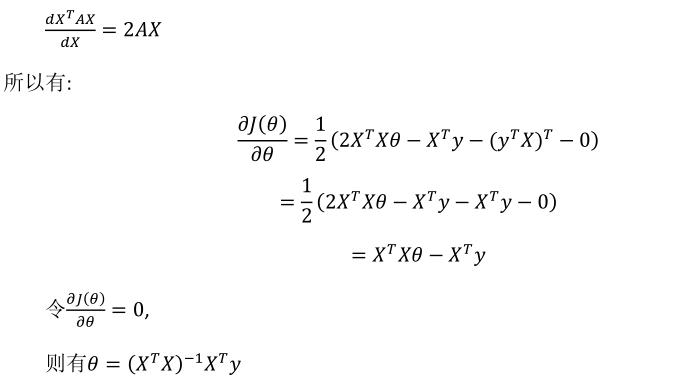
linux内核下载地址: https://www.kernel.org/pub/linux/kernel




