数值分析实验之线性方程组的迭代求解(java实现)

一、实验目的

 1．借助矩阵按模最大特征值，判断解方程组的Jacobi迭代法所得迭代序列的敛散性。

 2．会在Jacobi迭代法所得迭代序列收敛时，用修改后的Gauss-Seidel迭代法。

 3．会逐次超松驰迭代法。

二、实验原理

     

 

三、实验程序

    

 

四、实验内容

  用上面前二种方法求解如下4元线性方程组的近似解，所选方程组尽可能可以用多种方法求得收敛解。

  

 

 

   注：要注意判断迭代法收敛性，方法之一就是用程序求矩阵的按模最大特征值。

五、java源码

package shuzhifenxi;



import java.util.Scanner;
public class J {
 static int n = 4;
 public static void main(String[] args) {
  float[][] A = { { 10, -1, 2,  0 }, { -1, 11, -1,3 },
    { 2, -1, 10, -1 }, {  0, 3, -1, 8 } };
  float[] B = { 6, 25, -11, 15 };
  float e, m, temp, t;
  float y[] = { 0.0f, 0.0f, 0.0f, 0.0f }, 
  x0[] = { 0.0f,0.0f, 0.0f, 0.0f },
  x[] = { 0.0f, 0.0f, 0.0f, 0.0f };
  int N, i, j, k,sum1,sum2;
  System.out.println("输入要求的精度e=");
  Scanner scan = new Scanner(System.in);
  e = scan.nextFloat();
  System.out.println("最大迭代次数N=");
  N = scan.nextInt();
  for (i = 0; i < n; i++) {
   System.out.println("x0" + "[" + i + "]=" + x0[i]);
  }
  System.out.println("*************************************");
  System.out.println("以下是Jacobi迭代过程");
  System.out.println("*************************************");
  for (k = 0; k < N; k++) {
   m = 0;
   for (i = 0; i < n; i++) {
    x[i] = B[i];
    for (j = 0; j < n; j++)
     if (j != i) {
      x[i] = x[i] - A[i][j] * x0[j];
     }
    x[i] = x[i] / A[i][i];
    System.out.println("x[]" + x[i]);
    temp = Math.abs(x[i] - x0[i]);
    System.out.println("temp" + temp);
    if (temp > m)
     m = temp;
   }
   System.out.print(k + 1 + "次迭代:");
   
    
   for (int i1 = 0; i1 < n; i1++) {
          System.out.println("x" + "[" + i1 + "]=" + x[i1]);
    x0[i1] = x[i1];
   }
   if (m < e) {
    sum1=k+1;
    System.out.println("Jacobi迭代结束");
    System.out.println("一共迭代了"+sum1+"次");
    break;
   }
   
  }
  
  if (k > N)
  System.out.println("第" + k + "次迭代未找出满足精度的解 发散");
  System.out.println("\n");
  System.out.println("*************************************");
  System.out.println("以下是Gauss-Seidel迭代");
  System.out.println("*************************************");
  for (k = 0; k < N; k++) {
   m = 0;
   for (i = 0; i < n; i++) {
    t=y[i];
    y[i] = B[i];
    for (j = 0; j < n; j++)
     if (j != i) {
      y[i] = y[i] - A[i][j] * y[j];
     }
    y[i] =y[i] / A[i][i];
    temp = Math.abs(y[i] - t);
    System.out.println("temp" + temp);
    if (temp > m)
     m = temp;
   }
   System.out.print(k + 1 + "次迭代:");
   for (int i1 = 0; i1 < n; i1++) {
          System.out.println("x" + "[" + i1 + "]=" + y[i1]);
   }
   if (m < e) {
    sum2=k+1;
    System.out.println("Gauss-Seidel迭代结束");
    System.out.println("一共迭代了"+sum2+ "次"); 
    break;
   }
   
   if (k > N)
    System.out.println("第" + k + "次迭代未找出满足精度的解 发散");
         
  }
  
     
     }
}

   运行结果：

  Jacobi迭代：          

   

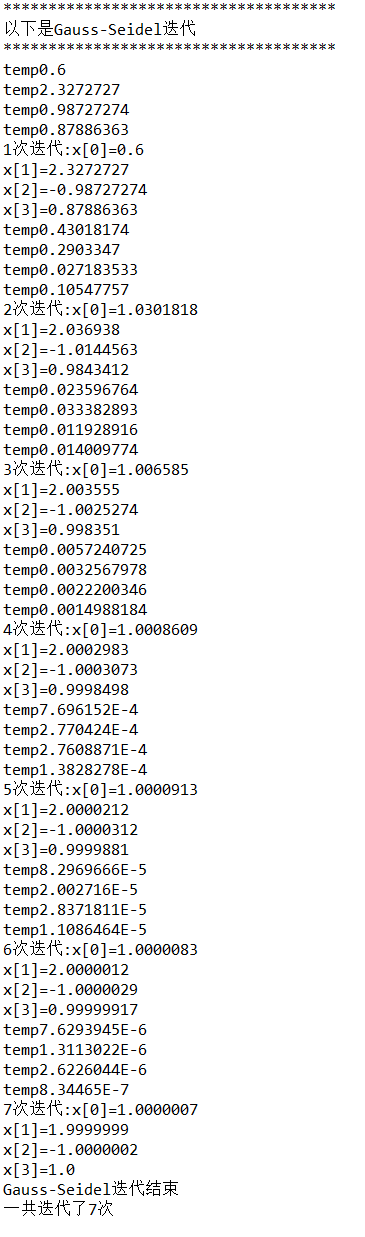
Gauss-Seidel迭代