一、实验目的
在己知f(x),x∈[a,b]的表达式,但函数值不便计算或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时,按插值原则f(xi)=yi (i=0,1,……, n)求出简单函数P(x)(常是多项式),使其在插值基点xi处成立(xi)= yi(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).
二、实验原理
三、实验内容
求f(x)=x4在[0,2]上按5个等距节点确定的Lagrange插值多项式
四、实验程序
(1).m文件
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标,Y是纵坐标,
%x是以向量形式输入的m个插值点,M在[a,b]上满足|f~(n+1)(x)|≤M
%注:f~(n+1)(x)表示f(x)的n+1阶导数
%输出的量:向量y是向量x处的插值,误差限R,n次牛顿插值多项式L及其系数向量C,
%差商的矩阵A
function[y,R,A,C,L] = newton(X,Y,x,M)
n = length(X);
m = length(x);
for t = 1 : m
z = x(t);
A = zeros(n,n);
A(:,1) = Y';
s = 0.0; p = 1.0; q1 = 1.0; c1 = 1.0;
for j = 2 : n
for i = j : n
A(i,j) = (A(i,j-1) - A(i-1,j-1))/(X(i)-X(i-j+1));
end
q1 = abs(q1*(z-X(j-1)));
c1 = c1 * j;
end
C = A(n, n); q1 = abs(q1*(z-X(n)));
for k = (n-1):-1:1
C = conv(C, poly(X(k)));
d = length(C);
C(d) = C(d) + A(k,k);%在最后一维,也就是常数项加上新的差商
end
y(t) = polyval(C,z);
R(t) = M * q1 / c1;
end
L = poly2sym(C);
(2)命令窗口输入
X = [0 0.5 1.0 1.5 2.0];
Y = [0 0.0625 1 5.0625 16];
x = linspace(0,pi,50);
M = 1;
[y,R,A,C,L] = newton(X, Y, x, M);
y1 = x.*x.*x.*x; %可根据所给函数更改
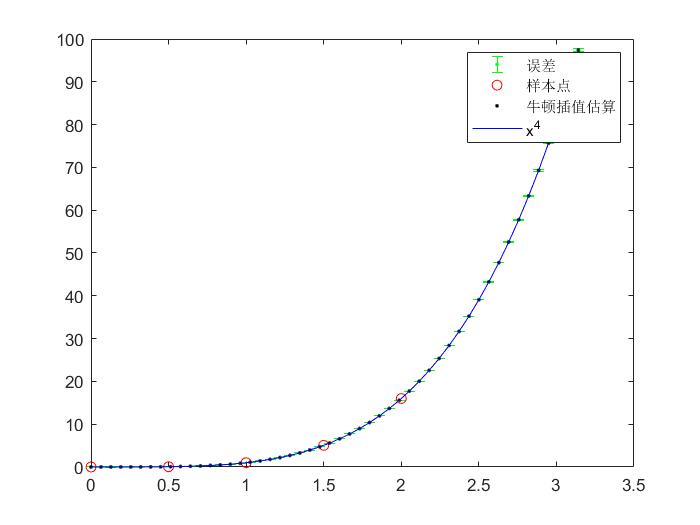
errorbar(x,y,R,'.g')
hold on
plot(X, Y, 'or', x, y, '.k', x, y1, '-b');
legend('误差','样本点','牛顿插值估算','x^4');
五、运算结果
(1) 图像
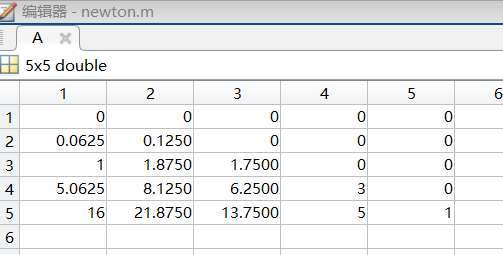
(2) 运算结果
第一列为所得多项式系数:

 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号