被难题分享
染色
\(\bf Description\)
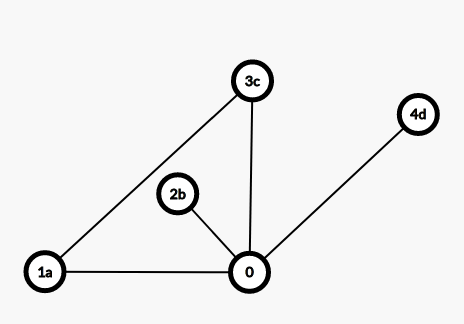
一个平面图，只有与坐标轴平行的边和成45°的边，构造一个四色的染色方案。
\(\bf Solution\)
按照从上到下，从左到右的顺序染色，每个点被染到的时候最多会连向四个点，显然我们只需要考虑这四个点颜色不同的情况。假设这四种颜色是abcd。
如果我们要将当前这个点染成a，那么我们要将a改成c，然后顺着这条路，把a和c翻转（实际上并不是一条路，而是一个二分图），如果沿着这条路走不会从1号点走到3号点，那么由于1号点连出去的是个二分图，直接全部翻转就好了。否则的话我们发现由于这是一个平面图，那么2号点和4号点是不会连上的，于是可以随便翻转一边。
【清华集训2014】矩阵变换
实际上就是给每行匹配一个数，我们让 \(pos[i][j]\) 表示 \(i\) 这个数在第 \(j\) 行的位置。假设第 \(i\) 行匹配的数是 \(x\) ，那么要满足对于所有 \(pos[x][j]>pos[x][i]\) 的行 \(j\) ，需要有 \(pos[match[j]][j]<pos[x][j]\)，这实际上就是一个稳定婚姻问题。（稳定婚姻的要求就是不能双飞）
周指导讲的东西
引入问题
一个 \(n \times kn\) 的格子，从左下角走到右上角，不能经过 \(y=kx\) ，求方案数。
一般化问题的解法
给定数列 \(a\) ，对于任意经过的 \((x,y)\) ，要满足 \(y \leq a_x\) 。
先把 \(a_i\) 取个前缀min显然不影响答案。
用 \(f(L,R,U,D)\) 表示在这一块里从最下面一行走到最右面一列的方案数。
取 \(mid=\frac{L+R}{2}\) ，左下和右上变成了更小的子问题，右下角那一块是没有限制的，可以FFT优化一下，系数大概就是一堆组合数？
丑陋而莫名其妙的图片。。
这样是两个log的。
回到最开始的问题，由于子问题是一样的，于是发现可以倍增FFT做了。
更优良的做法
OEIS一下
封闭形式是 \({kn+n \choose n}/(kn+1)\) （不是很确定）
生成函数是 \(G(x)=1+xG^{k+1}(x)\) ，组合意义并没有理解。。
然后封闭形式的话，《具体数学》P302-305
首先搞一个数列 \(a\) ，其中 \(a_i \in \mathbb Z\)，并且 \(\sum a_i=1\)，而且要满足 \(a\) 的所有前缀和 \(>0\)
可以发现一些性质：在 \(a\) 的所有轮换中，只有 \(a\) 是满足后面那个条件的。并且不会出现 \(a\) 及其所有轮换都不满足后面那个条件的情况。
对于卡特兰数，可以认为 \(a\) 的取值是 \(n\) 个 \(1\) 和 \(n\) 个 \(-1\)，并且为了从 \(\geq 0\) 变成 \(>0\) 我们在前面加一个 \(1\)，一个符合条件的数列有 \(2n+1\) 个轮换，于是就很容易得到方案数是
推广到 \(n \times kn\) 的方格，我们认为向右走是 \(+k\) ，向上走是 \(-1\) ，类比卡特兰数就可以得到方案数是
然后就可以切题了？
em，这东西好像叫Raney定理。。
此人很懒，没有留下签名。
