博弈题目小结
HDU 2174 kiki's game
题意:有一个N*M的棋盘,起点在右上角,两个人每轮可把棋子向左、向下或者向左下移动一格,直到不能移动棋子者输。
NP图解决:
概念:
必败点(P点):前一个选手将取胜的位置称为必败点。
必胜点(N点):下一个选手将取胜的位置成为必胜点。
性质:

步骤:

NP图:
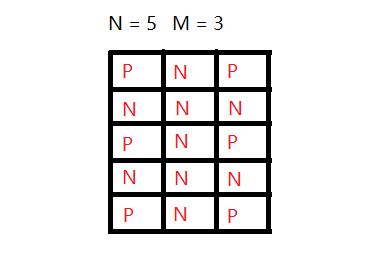
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 12 int main() 13 { 14 int a, b; 15 while(~scanf("%d %d", &a, &b)){ 16 if(a == 0 && b == 0) break; 17 if(a%2 == 1 && b%2 == 1) puts("What a pity!"); 18 else puts("Wonderful!"); 19 } 20 return 0; 21 }
HDU 2149 Public Sale
题意:
底价为 0,最低成交价为 M,两位博弈,每轮叫价区间 1~N
求 先手开始有多少种取胜叫价,输出每种叫价值。
解题思路:
巴什博弈变形,只要能把 (N+1) * t 留给对手必胜,如果自己是(N+1)*r 必败。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 12 int main() 13 { 14 int N, M; 15 while(~scanf("%d %d", &M, &N)){ 16 if(M <= N){ 17 for(int i = M; i <= N; i++){ 18 printf("%d%c", i, i==N?'\n':' '); 19 } 20 } 21 else if(M%(N+1) == 0) puts("none"); 22 else{ 23 printf("%d\n", M%(N+1)); 24 } 25 } 26 return 0; 27 }
HDU 1907 John
题意:
有 N 堆物品,每轮选着一堆拿走若干物品,拿走最后一个物品的输;
解题思路:
Nim博弈变形,异或判断是否为奇异局势, 面对奇异局势先手必败,如果全是 1 判断奇偶性,偶数则先手胜。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 char ans1[] = "John", ans2[] = "Brother"; 12 int main() 13 { 14 int N, sum; 15 bool flag = false; 16 int T_case, tp; 17 scanf("%d", &T_case); 18 while(T_case--){ 19 flag = false; 20 scanf("%d", &N);scanf("%d", &sum); 21 if(sum > 1) flag = true; 22 inc(i, 2, N){ 23 scanf("%d", &tp); 24 if(tp > 1) flag = true; 25 sum^=tp; 26 } 27 if(!flag) printf("%s", N%2?ans2:ans1); 28 else printf("%s", sum==0?ans2:ans1); 29 puts(""); 30 } 31 return 0; 32 }
HDU 2509 Be the Winner
题意:同上;
解题思路:同上;
HDU 1850 Being a Good Boy in Spring Festival
题意:有 N 堆 扑克牌,每轮选择其中一堆拿走任意张牌,拿走最后一张牌的胜,问先手如果想取胜,第一步有多少种选择?
解题思路:
Nim博弈变形;
原理、方法都很详细:https://www.cnblogs.com/kuangbin/archive/2011/11/24/2262389.html
即枚举每一堆是否可以删掉一些值维持最后 NIM 游戏的状态, NIM 游戏的最后状态是唯一不变的。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 const int MAXN = 2e5+10; 12 int tp[MAXN]; 13 int main() 14 { 15 int N, sum = 0; 16 while(~scanf("%d", &N) && N){ 17 int ans = 0; 18 scanf("%d", &sum); 19 tp[1] = sum; 20 inc(i, 2, N){ 21 scanf("%d", &tp[i]); 22 sum^=tp[i]; 23 } 24 inc(i, 1, N){ 25 if(tp[i] > (sum^tp[i])) ans++; 26 } 27 printf("%d\n", ans); 28 } 29 return 0; 30 }
HDU 1536 S-Nim
题意:
给出一个集合 S 表示游戏中可选的数目,接下来给定 M 个游戏局面即 N 堆物品的大小。两人轮流选择一堆取数 只能取 ∈S 的数目,取走最后一个胜。判断游戏局面是先手胜还是后手胜。
题目给出了SG函数的用途和求法。
解题思路:
SG函数模板。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 const int MAXN = 2e3+10; 12 const int MM = 1e4+5; 13 int S[MAXN], sg[MM]; 14 int vis[MM]; 15 string ans; 16 17 void getsg(int n) 18 { 19 sg[0] = 0; 20 memset(vis, -1, sizeof(vis)); 21 inc(i, 1, MM){ 22 inc(j, 1, n){ 23 if(S[j] > i) break; 24 vis[sg[i-S[j]]] = i; 25 } 26 // puts("zjj"); 27 int k = 0; 28 while(vis[k] == i) k++; 29 sg[i] = k; 30 } 31 } 32 33 int main() 34 { 35 int N, M, K, tp, res; 36 37 while(~scanf("%d", &N) && N){ 38 ans = ""; 39 inc(i, 1, N) scanf("%d", &S[i]); 40 //inc(i, 1, N) printf("%d ", S[i]); 41 sort(S+1, S+N+1); 42 getsg(N); 43 // puts("zjj"); 44 scanf("%d", &K); 45 while(K--){ 46 scanf("%d", &M); 47 // scanf("%d", &res); 48 res = 0; 49 inc(i, 1, M){ 50 scanf("%d", &tp); 51 res^=sg[tp]; 52 } 53 if(res == 0) ans+='L'; 54 else ans+='W'; 55 } 56 cout << ans << endl; 57 } 58 59 return 0; 60 }
HDU 1849 Rabbit and Grass
题意:一维棋盘,给出每个棋子的初始位置,两人轮流选择一个棋子走到左边任意点。
解题思路:NIM游戏,把棋子移动看成取石子。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 12 int main() 13 { 14 int N, ans, tp; 15 while(~scanf("%d", &N) && N){ 16 ans = 0; 17 inc(i, 1, N){ 18 scanf("%d", &tp); 19 ans^=tp; 20 } 21 if(!ans) puts("Grass Win!"); 22 else puts("Rabbit Win!"); 23 } 24 return 0; 25 }
HDU 1851 A Simple Game
题意:N堆物品,每堆每次最多取L个,每人轮流取东西,取走最后那个的获胜。
解题思路: NIM游戏,每一堆单独作为一个NIM游戏 M%L若为0 先手输,否则后手输, 因为双方都采取最佳策略,所以最后把每一堆的结果异或起来即可。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 12 int main() 13 { 14 int N, ans, tp; 15 while(~scanf("%d", &N) && N){ 16 ans = 0; 17 inc(i, 1, N){ 18 scanf("%d", &tp); 19 ans^=tp; 20 } 21 if(!ans) puts("Grass Win!"); 22 else puts("Rabbit Win!"); 23 } 24 return 0; 25 }
HDU 2897 邂逅明下
题意:一堆大小为 N 的物品,两人轮流取物品,取值范围 [ p, q ], 若堆物品的数量小于等于 p 则该轮需要全部取走,取走最后物品的败,先手是否能取胜。
解题思路:Bash博弈变形 如果当前 N == (p+q)*r 先手必胜,因为 先手先取 q 个,接下来每次后手取 k 个,先手取(p+q)-k , 最后剩下一个 p 给后手 ;
如果当前 N == (p+q)*r + res, 若 p < res 则 先手胜,先手一开始取 res-p 个, 接下来后手每次取 k 个,先手取 (p+q)-k 个,最后留给后手的肯定 等于 p;
若 res < p 则后手胜, 因为无论 先手取 k ,后手取 (p+q)-k ,最后把 res 留给先手。
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 12 int main() 13 { 14 int N, p, q; 15 while(~scanf("%d %d %d", &N, &p, &q)){ 16 int res = N%(p+q); 17 if(res == 0 || (res > p && res < p+q)) puts("WIN"); 18 else puts("LOST"); 19 } 20 return 0; 21 }
HDU 2516 取石子游戏
题意:有一堆大小为 N 的石子,第一轮可以取任意数量的石子,但不能全取,接下来每一轮只能取不超过上一轮取数得两倍的石子,没有石子取得输。
解题思路:
斐波那契博弈(Fibonacci Nim)
有一堆个数为n(n>=2)的石子,游戏双方轮流取石子,规则如下:
1)先手不能在第一次把所有的石子取完,至少取1颗;
2)之后每次可以取的石子数至少为1,至多为对手刚取的石子数的2倍。
约定取走最后一个石子的人为赢家,求必败态。
结论:当n为Fibonacci数的时候,必败。
f[i]:1,2,3,5,8,13,21,34,55,89……
AC code:

1 #include <bits/stdc++.h> 2 #define inc(i, j, k) for(int i = j; i <= k; i++) 3 #define rep(i, j, k) for(int i = j; i < k; i++) 4 #define F(x) ((x)/3+((x)%3==1?0:tb)) 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 #define MEM(i, j) memset(i, j, sizeof(i)); 9 #define gcd(i, j) __gcd(i, j) 10 using namespace std; 11 const int MAXN = 50; 12 LL m[MAXN]; 13 int main() 14 { 15 m[0] = 0; 16 m[1] = 1; 17 m[2] = 2; 18 for(int i = 3; i < MAXN; i++){ 19 m[i] = m[i-1]+m[i-2]; 20 // cout << m[i] << endl; 21 } 22 // printf("%d\n", m[MAXN-1]); 23 LL N; 24 while(~scanf("%lld", &N) && N){ 25 bool flag = true; 26 for(int i = 0; i < MAXN; i++){ 27 if(m[i] == N){ 28 flag = false; 29 } 30 } 31 if(flag) puts("First win"); 32 else puts("Second win"); 33 34 } 35 return 0; 36 }
HDU 1847 Good Luck in CET-4 Everybody!
题意:N 堆物品,两人轮流取,只能取 2的幂次倍, 取走最后一个的胜。
解题思路: NP分析,必败点为 0,从必败点加任意一个二次幂都是必胜点,即必胜点一定可以删掉一个二次幂变成一个必败点。
所以这题类似于素数筛,从小的 P点 开始筛 N 点,遍历过去如果遇到未被前面筛掉的点必定为 P 点(因为未被前面的 P 点筛到,说明当前点的值由两个 N 点组成,所以无论 当前点如何作差最后都是变成 一个 N 点,后手必胜),所以直接筛过去是合理的。
AC code:

1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <cmath> 5 #include <cstdio> 6 #include <string> 7 #include <vector> 8 #include <cstdlib> 9 #include <cstring> 10 #include <iostream> 11 #include <algorithm> 12 #define inc(i, j, k) for(int i = j; i <= k; i++) 13 #define rep(i, j, k) for(int i = j; i < k; i++) 14 #define F(x) ((x)/3+((x)%3==1?0:tb)) 15 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 16 #define INF 0x3f3f3f3f 17 #define LL long long 18 #define MEM(i, j) memset(i, j, sizeof(i)); 19 #define gcd(i, j) __gcd(i, j) 20 using namespace std; 21 const int MAXN = 1e3+10; 22 bool f[MAXN]; 23 void init() 24 { 25 MEM(f, 0); 26 rep(i, 0, MAXN){ 27 if(!f[i]){ 28 int tp = 1; 29 while(i+tp < MAXN){ 30 f[i+tp] = true; 31 tp<<=1; 32 } 33 } 34 } 35 } 36 37 int main() 38 { 39 int N; 40 init(); 41 while(~scanf("%d", &N)){ 42 if(f[N]) puts("Kiki"); 43 else puts("Cici"); 44 } 45 return 0; 46 }
HDU 1079 Calendar Game
题意:给定一个起始日期,可以跳到下个月的这一天或者下一天,如果下个月没有这一天就只能跳到下一天。最后恰好跳到 2001/11/04 的人获胜,超过这个日期的会失败。
解题思路:NP分析,可以直接找规律,也可以直接记忆化搜索转移状态。
AC code:

1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <cmath> 5 #include <cstdio> 6 #include <string> 7 #include <vector> 8 #include <cstdlib> 9 #include <cstring> 10 #include <iostream> 11 #include <algorithm> 12 #define inc(i, j, k) for(int i = j; i <= k; i++) 13 #define rep(i, j, k) for(int i = j; i < k; i++) 14 #define F(x) ((x)/3+((x)%3==1?0:tb)) 15 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 16 #define INF 0x3f3f3f3f 17 #define LL long long 18 #define MEM(i, j) memset(i, j, sizeof(i)); 19 #define gcd(i, j) __gcd(i, j) 20 using namespace std; 21 const int MAXN = 2e3+10; 22 int dat[MAXN][50][50]; 23 int da[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; 24 bool check(int yy, int mm, int dd) 25 { 26 if(mm > 12) return false; 27 if(((yy%4==0 && yy%100!=0) || yy%400==0) && mm == 2 && dd <= 29) return true; 28 if(da[mm] < dd) return false; 29 return true; 30 } 31 32 int solve(int yy, int mm, int dd) 33 { 34 if(dat[yy][mm][dd] != -1) return dat[yy][mm][dd]; 35 if(yy > 2001) return dat[yy][mm][dd] = 1; 36 if(yy == 2001 && mm > 11) return dat[yy][mm][dd] = 1; 37 if(yy == 2001 && mm == 11 && dd > 4) return dat[yy][mm][dd] = 1; 38 if(yy == 2001 && mm == 11 && dd == 4) return dat[yy][mm][dd] = 0; 39 40 int ty = yy, tm = mm, td = dd; 41 td++; 42 if(((yy%4==0 && yy%100!=0) || yy%400==0) && tm == 2){ 43 if(td > 29){ 44 td = 1; 45 tm++; 46 } 47 if(solve(ty, tm, td) == 0) return dat[yy][mm][dd] = 1; 48 } 49 else{ 50 if(da[tm] < td){ 51 td = 1; 52 tm++; 53 } 54 if(tm > 12) tm = 1, ty++; 55 if(solve(ty, tm, td) == 0) return dat[yy][mm][dd] = 1; 56 } 57 58 ty = yy, tm = mm, td = dd; 59 tm++; 60 if(tm > 12) ty++, tm = 1; 61 if(check(ty, tm, td) && solve(ty, tm, td) == 0) return dat[yy][mm][dd] = 1; 62 63 return dat[yy][mm][dd] = 0; 64 65 } 66 67 int main() 68 { 69 MEM(dat, -1); 70 int T_case, y, m, d; 71 scanf("%d", &T_case); 72 while(T_case--){ 73 scanf("%d %d %d", &y, &m, &d); 74 if(solve(y, m, d)) puts("YES"); 75 else puts("NO"); 76 } 77 return 0; 78 } 79 80 // (天数+日数)偶数是真,奇数是假,例外:9/30 11/30 81 //#include <set> 82 //#include <map> 83 //#include <queue> 84 //#include <cmath> 85 //#include <cstdio> 86 //#include <string> 87 //#include <vector> 88 //#include <cstdlib> 89 //#include <cstring> 90 //#include <iostream> 91 //#include <algorithm> 92 //#define inc(i, j, k) for(int i = j; i <= k; i++) 93 //#define rep(i, j, k) for(int i = j; i < k; i++) 94 //#define F(x) ((x)/3+((x)%3==1?0:tb)) 95 //#define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) 96 //#define INF 0x3f3f3f3f 97 //#define LL long long 98 //#define MEM(i, j) memset(i, j, sizeof(i)); 99 //#define gcd(i, j) __gcd(i, j) 100 //using namespace std; 101 //int main() 102 //{ 103 // int T_case; 104 // int yy,mm,dd; 105 // scanf("%d",&T_case); 106 // while(T_case--) 107 // { 108 // scanf("%d%d%d",&yy,&mm,&dd); 109 // if( (dd+mm)%2 == 0 || (mm == 9 && dd == 30) || (mm == 11 && dd == 30) ) puts("YES"); 110 // else puts("NO"); 111 // } 112 // return 0; 113 //}


